目錄

快慢指針：

1. 相交鏈表（簡單）

2. 環形鏈表（簡單）

3. 快樂數（簡單）

4. 環形鏈表 II（中等）

5. 刪除鏈表的倒數第 N 個節點（中等）

遞歸迭代雙解法：

1. 合并兩個有序鏈表（簡單）

1.1 遞歸求解

1.2 迭代求解

2. 反轉鏈表（簡單）

2.1 遞歸求解

2.2 迭代求解

3. 兩兩交換鏈表中的節點（中等）

3.1 遞歸求解

3.2 迭代求解

4. 合并 K 個升序鏈表（困難）

4.1 遞歸解法

4.2 迭代解法

綜合題：

1. 隨機鏈表的復制（中等）

2. 重排鏈表（中等）

3. K個一組翻轉鏈表（困難）

---

快慢指針：

1. 相交鏈表（簡單）

找兩個鏈表的尾結點，尾結點不相同則不相交。假設相交，長短鏈表之間差距gap步。假設i指向長鏈表的頭節點，j指向短鏈表的頭節點，i先走gap步，然后ij同時走，每次走1步。當ij相遇時，相遇點就是相交點。

class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {// 找兩個鏈表的尾結點，尾結點不相同則不相交ListNode* tailA = headA;ListNode* tailB = headB;int lenA = 0;int lenB = 0;while (tailA->next){++lenA;tailA = tailA->next;}while (tailB->next){++lenB;tailB = tailB->next;}if (tailA != tailB)return nullptr;// 判斷長短鏈表ListNode* longList = headA;ListNode* shortList = headB;if (lenB > lenA){longList = headB;shortList = headA;}// 長鏈表先走gap步int gap = abs(lenA - lenB);while (gap--){longList = longList->next;}// 同時走，找交點while (longList != shortList){longList = longList->next;shortList = shortList->next;}return longList;}
};

2. 環形鏈表（簡單）

慢指針每次走1步，快指針每次走2步，慢指針進環后，快指針一定能追上慢指針，它們會在環中某點相遇。

為什么慢指針每次走1步，快指針要每次走2步，它們才能相遇？

假設慢指針進環時，快慢指針之間差距gap步。

如果快指針每次走2步，每走一次，它們之間的差距減1，gap一定會減到0。

如果快指針每次走3步，每走一次，它們之間的差距減2。如果gap為偶數，gap一定會減到0。如果gap為奇數，gap會減到-1，表示它們之間的距離變成C - 1（C是環的周長），如果C - 1是偶數，它們會相遇，如果C - 1是奇數，它們永遠不會相遇。

class Solution {
public:bool hasCycle(ListNode *head) {ListNode* slow = head;ListNode* fast = head;while (fast && fast->next){slow = slow->next;fast = fast->next->next;if (slow == fast)return true;}return false;}
};

3. 快樂數（簡單）

不是鏈表題，但是和上一題“環形鏈表”類似，慢指針每次走1步，快指針每次走2步，慢指針進環后，快指針一定能追上慢指針，它們會在環中某點相遇。如果相遇點為1，則為快樂數，否則不是快樂數。這里的指針表示的是值本身。

class Solution {
public:bool isHappy(int n) {int slow = n;int fast = bitSquareSum(n);while (slow != fast){slow = bitSquareSum(slow);fast = bitSquareSum(bitSquareSum(fast));}return slow == 1;}private:// 計算n的每一位的平方和int bitSquareSum(int n){int sum = 0;while (n){int tmp = n % 10;sum += tmp * tmp;n /= 10;}return sum;}
};

4. 環形鏈表 II（中等）

慢指針每次走1步，快指針每次走2步，慢指針進環后，快指針一定能追上慢指針，它們會在環中某點相遇。

假設在相遇點，慢指針一共走了k步，那么快指針一定一共走了2k步，所以快指針比慢指針多走了k步。另外，在相遇點，快指針一定比慢指針在環中多走了若干圈。所以，k一定是環的周長（環中節點個數）的整數倍。

此時，讓i指向相遇點，j指向鏈表頭節點，它們之間差距k步（慢指針走過的步數），如果i到達了環的入口，j也一定到達了環的入口，因為它們之間差距k步，k一定是環的周長的整數倍。

class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while (fast && fast->next){fast = fast->next->next;slow = slow->next;if (fast == slow) // 相遇{ListNode* i = slow; // 相遇點ListNode* j = head;while (i != j){i = i->next;j = j->next;}return i;}}return nullptr;}
};

5. 刪除鏈表的倒數第 N 個節點（中等）

快指針先走n步，然后快慢指針同時走，每次走1步。當快指針指向最后一個節點時，慢指針指向倒數第n + 1個節點。

例如，刪除鏈表的倒數第2個節點：

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* preHead = new ListNode(0, head); // 哨兵節點ListNode* fast = preHead; // 快指針ListNode* slow = preHead; // 慢指針// 快指針先走n步while (n--){fast = fast->next;}// 快慢指針同時走，每次走1步，直到快指針走到最后一個節點停止while (fast->next){fast = fast->next;slow = slow->next;}// 此時慢指針指向倒數第n+1個節點// 讓倒數第n+1個節點的next域直接指向倒數第n-1個節點slow->next = slow->next->next;return preHead->next;}
};

遞歸迭代雙解法：

1. 合并兩個有序鏈表（簡單）

1.1 遞歸求解

重復的子問題——函數頭設計

ListNode*?mergeTwoLists(ListNode*?list1,?ListNode*?list2)

子問題在做什么——函數體設計

選擇兩個鏈表的頭節點中值較小的那一個作為最終合并的新鏈表的頭節點，然后將剩下的鏈表交給遞歸函數去處理。

1. 比較list1->val和list2->val的大小（假設list1->val較小）
2. list1->next?=?mergeTwoLists(list1->next,?list2);
3. return list1;

遞歸出口

當某一個鏈表為空的時候，返回另外一個鏈表。

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (list1 == nullptr)return list2;if (list2 == nullptr)return list1;if (list1->val < list2->val){list1->next = mergeTwoLists(list1->next, list2);return list1;}else{list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};

1.2 迭代求解

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {ListNode* preHead = new ListNode; // 哨兵節點ListNode* tail = preHead;// 取小的尾插while (list1 && list2){if (list1->val < list2->val){tail->next = list1;tail = tail->next;list1 = list1->next;}else{tail->next = list2;tail = tail->next;list2 = list2->next;}}if (list1){tail->next = list1;}if (list2){tail->next = list2;}return preHead->next;}
};

2. 反轉鏈表（簡單）

2.1 遞歸求解

重復的子問題——函數頭設計

ListNode*?reverseList(ListNode*?head)

子問題在做什么——函數體設計

將當前結點之后的鏈表反轉，然后把當前結點添加到反轉后的鏈表后面即可，返回反轉后的頭節點。

1. ListNode* newHead = reverseList(head->next);
2. head->next->next = head;? ? head->next?=?nullptr;
3. return?newHead;

遞歸出口

當前結點為空或者當前只有一個結點的時候，不用反轉，直接返回。

class Solution {
public:ListNode* reverseList(ListNode* head) {if (head == nullptr || head->next == nullptr)return head;ListNode* newHead = reverseList(head->next);head->next->next = head;head->next = nullptr;return newHead;}
};

2.2 迭代求解

class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* pre = nullptr;ListNode* cur = head;while (cur){ListNode* next = cur->next;cur->next = pre;pre = cur;cur = next;}return pre;}
};

3. 兩兩交換鏈表中的節點（中等）

3.1 遞歸求解

重復的子問題——函數頭設計

ListNode*?swapPairs(ListNode*?head)

子問題在做什么——函數體設計

將從第三個節點開始的鏈表兩兩交換節點，然后再把前兩個節點交換一下，鏈接上剛才處理過的鏈表，并返回。

1. ListNode*?tmp?=?swapPairs(head->next->next);
2. ListNode*?newHead?=?head->next;? ? newHead->next?=?head;
3. head->next?=?tmp;
4. return?newHead;

遞歸出口

當前結點為空或者當前只有一個結點的時候，不用兩兩交換，直接返回。

class Solution {
public:ListNode* swapPairs(ListNode* head) {if (head == nullptr || head->next == nullptr)return head;ListNode* tmp = swapPairs(head->next->next);ListNode* newHead = head->next;newHead->next = head;head->next = tmp;return newHead;}
};

3.2 迭代求解

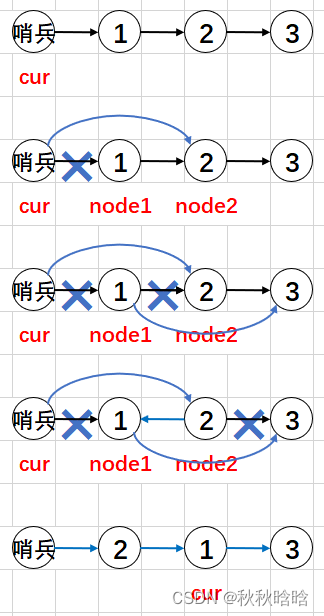
class Solution {
public:ListNode* swapPairs(ListNode* head) {ListNode* preHead = new ListNode(0, head); // 哨兵節點ListNode* cur = preHead;// cur后面的兩個節點交換while (cur->next && cur->next->next){ListNode* node1 = cur->next;ListNode* node2 = cur->next->next;cur->next = node2;node1->next = node2->next;node2->next = node1;cur = node1;}return preHead->next;}
};

4. 合并 K 個升序鏈表（困難）

4.1 遞歸解法

分治的思想，類似歸并排序：

1. 劃分兩個子區間

2. 分別對兩個子區間的鏈表進行合并，形成兩個有序鏈表

3. 合并兩個有序鏈表

重復的子問題——函數頭設計

ListNode*?merge(vector<ListNode*>& lists, int begin, int end)

子問題在做什么——函數體設計

1. 劃分兩個子區間：int mid = (begin + end) / 2;
2. 遞歸合并兩個子區間：
   ListNode* l1 = merge(lists, begin, mid);
   ListNode* l2 = merge(lists, mid + 1, end);
3. 合并兩個有序鏈表：return?mergeTowList(l1, l2);

遞歸出口

當區間只有一個鏈表時，不合并。另外，當題目給出空鏈表時，不合并。

class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {return merge(lists, 0, lists.size() - 1);}private:ListNode* merge(vector<ListNode*>& lists, int begin, int end){if (begin > end)return nullptr;if (begin == end)return lists[begin];int mid = (begin + end) / 2;ListNode* l1 = merge(lists, begin, mid);ListNode* l2 = merge(lists, mid + 1, end);return mergeTwoLists(l1, l2);}ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){ListNode* preHead = new ListNode; // 哨兵節點ListNode* tail = preHead;// 取小的尾插while (list1 && list2){if (list1->val < list2->val){tail->next = list1;tail = tail->next;list1 = list1->next;}else{tail->next = list2;tail = tail->next;list2 = list2->next;}}if (list1){tail->next = list1;}if (list2){tail->next = list2;}return preHead->next;}
};

4.2 迭代解法

和“合并兩個有序鏈表”類似，就是取小的尾插。怎么判斷K個鏈表未合并的頭節點中最小的那個？利用堆這個數據結構即可。把K個鏈表未合并的頭節點放進一個小根堆，堆頂就是最小的那個。

class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {// 創建小根堆priority_queue<ListNode*, vector<ListNode*>, cmp> heap;// 將所有頭節點放進小根堆for (auto& l : lists){if (l){heap.push(l);}}// 合并鏈表ListNode* preHead = new ListNode; // 哨兵節點ListNode* tail = preHead;while (!heap.empty()){// 取堆頂節點尾插tail->next = heap.top();heap.pop();tail = tail->next;// 將剛才合并的節點的下一個節點補充進堆if (tail->next){heap.push(tail->next);}}return preHead->next;}private:struct cmp{bool operator()(ListNode* n1, ListNode* n2){return n1->val > n2->val;}};
};

綜合題：

1. 隨機鏈表的復制（中等）

class Solution {
public:Node* copyRandomList(Node* head) {if (head == nullptr)return nullptr;// A->B->C->null --> A->A'->B->B'->C->C'->nullNode* cur = head;while (cur){Node* copy = new Node(cur->val); // 拷貝結點copy->next = cur->next;cur->next = copy;cur = cur->next->next;}// 設置拷貝結點的random，假如A的random域指向C，就讓A'的random域指向C'cur = head;while (cur){Node* copy = cur->next;if (cur->random == nullptr){copy->random = nullptr;}else{copy->random = cur->random->next;}cur = cur->next->next;}// 將A'、B'、C'鏈接在一起，并且還原原鏈表Node* preHead = new Node(0); // 哨兵節點Node* tail = preHead;cur = head;while (cur){tail->next = cur->next;tail = tail->next;cur->next = cur->next->next;cur = cur->next;}return preHead->next;}
};

2. 重排鏈表（中等）

把鏈表后半段反轉，再合并起來：

鏈表長度是偶數：1 2 3 4? ??（2是中間節點）

1 2

4 3

合并起來：1 4 2 3

鏈表長度是奇數：1 2 3 4 5? ??（3是中間節點）

1 2 3

5 4（4 5反轉）

合并起來：1 5 2 4 3

class Solution {
public:void reorderList(ListNode* head) {ListNode* mid = midNode(head);ListNode* l2 = reverseList(mid->next);mid->next = nullptr;ListNode* l1 = head;mergeLists(l1, l2);}private:// 快慢指針找鏈表的中間節點，如果節點個數為偶數，取靠左的ListNode* midNode(ListNode* head){ListNode* fast = head;ListNode* slow = head;// 慢指針每次走1步，快指針每次走2步// 如果節點個數為奇數，當快指針指向最后一個節點時，慢指針指向中間節點// 如果節點個數為奇數，當快指針指向倒數第二個節點時，慢指針指向靠左的中間節點while (fast->next && fast->next->next){fast = fast->next->next;slow = slow->next;}return slow;}// 反轉鏈表ListNode* reverseList(ListNode* head) {ListNode* pre = nullptr;ListNode* cur = head;while (cur){ListNode* next = cur->next;cur->next = pre;pre = cur;cur = next;}return pre;}// 合并鏈表void mergeLists(ListNode* l1, ListNode* l2){ListNode* cur1 = l1;ListNode* cur2 = l2;while (cur1 && cur2){ListNode* next1 = cur1->next;ListNode* next2 = cur2->next;cur1->next = cur2;cur2->next = next1;cur1 = next1;cur2 = next2;}}
};

3. K個一組翻轉鏈表（困難）

頭插法。

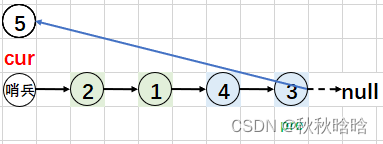
class Solution {
public:ListNode* reverseKGroup(ListNode* head, int k) {// 求出需要翻轉多少組int n = 0;ListNode* cur = head;while (cur){cur = cur->next;n++;}n /= k;// 重復n次：長度為k的鏈表翻轉ListNode* preHead = new ListNode; // 哨兵節點ListNode* pre = preHead;cur = head;for (int i = 0; i < n; i++){ListNode* tmp = cur;for (int j = 0; j < k; j++){ListNode* next = cur->next;cur->next = pre->next;pre->next = cur;cur = next;}pre = tmp;}// 把不需要翻轉的部分接上pre->next = cur;return preHead->next;}
};