from:https://blog.csdn.net/m399498400/article/details/52556168
?
定義本課程常用符號
訓練數據:機器用來學習的數據
測試數據:用來考察機器學習效果的數據,相當于考試。
m = 訓練樣本的數量(訓練集的個數)
x = 輸入的特征(例如房屋面積)
y = 輸出結果(例如房屋售價)
(x(i),y(i)) = 表示訓練集中第i個訓練樣本
一.Cost Function(代價函數)
一,什么是代價函數?
我在網上找了很長時間代價函數的定義,但是準確定義并沒有,我理解的代價函數就是用于找到最優解的目的函數,這也是代價函數的作用。
二,代價函數作用原理?
對于回歸問題,我們需要求出代價函數來求解最優解,常用的是平方誤差代價函數。
比如,對于下面的假設函數:?
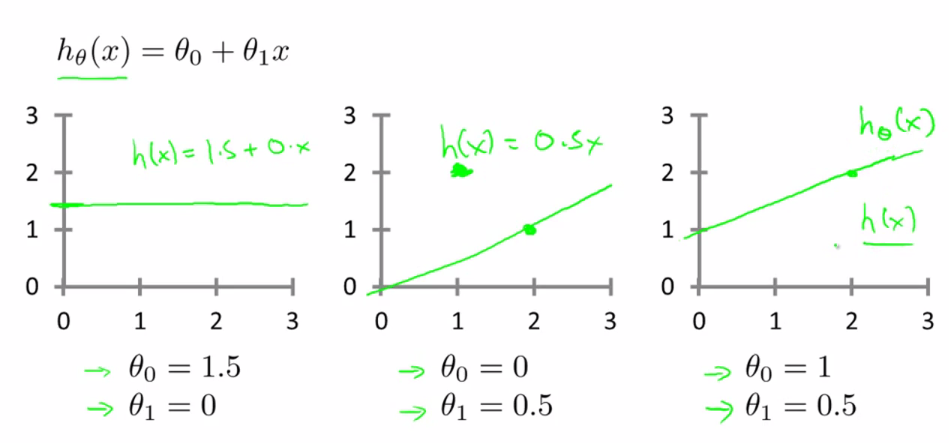
里面有θ0和θ1兩個參數,參數的改變將會導致假設函數的變化,比如:?
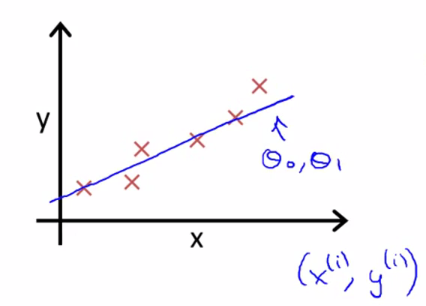
現實的例子中,數據會以很多點的形式給我們,我們想要解決回歸問題,就需要將這些點擬合成一條直線,找到最優的θ0和θ1來使這條直線更能代表所有數據。?
而如何找到最優解呢,這就需要使用代價函數來求解了,以平方誤差代價函數為例。?
從最簡單的單一參數來看,假設函數為:?
平方誤差代價函數的主要思想就是將實際數據給出的值(x(i),y(i))與我們擬合出的線的對應值做差,這樣就能求出我們擬合出的直線與實際的差距了。
為了使這個值不受個別極端數據影響而產生巨大波動,采用類似方差再取二分之一的方式來減小個別數據的影響。這樣,就產生了代價函數:?
【平均數:?![]() ?(n表示這組數據個數,x1、x2、x3……xn表示這組數據具體數值)
?(n表示這組數據個數,x1、x2、x3……xn表示這組數據具體數值)
方差公式:?![]() 】
】
【擬合出的線的對應值—實際數據給出的值(x(i),y(i))】
而最優解即為代價函數的最小值,根據以上公式多次計算可得到?
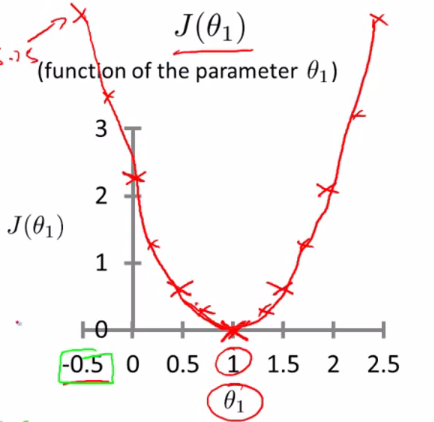
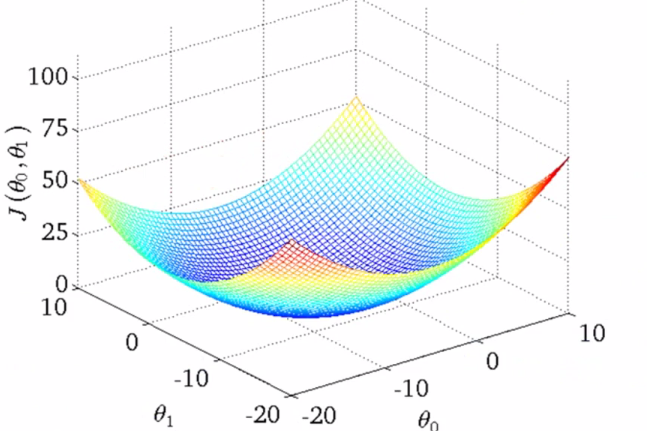
代價函數的圖像:?
可以看到該代價函數的確有最小值,這里恰好是橫坐標為1的時候。
如果更多參數的話,就會更為復雜,兩個參數的時候就已經是三維圖像了:?
高度即為代價函數的值,可以看到它仍然有著最小值的,而到達更多的參數的時候就無法像這樣可視化了,但是原理都是相似的。?
因此,對于回歸問題,我們就可以歸結為得到代價函數的最小值:?
?
二.Multivariate Linear regression(多元線性回歸)
現在起將開始介紹一種新的更為有效的線性回歸形式。這種形式適用于多個變量或者多特征量的情況。
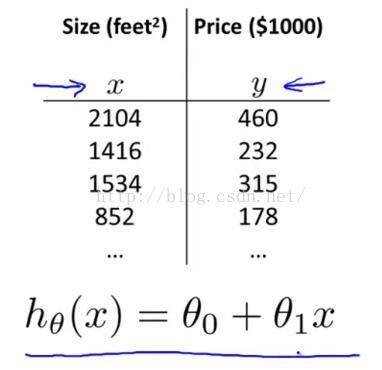
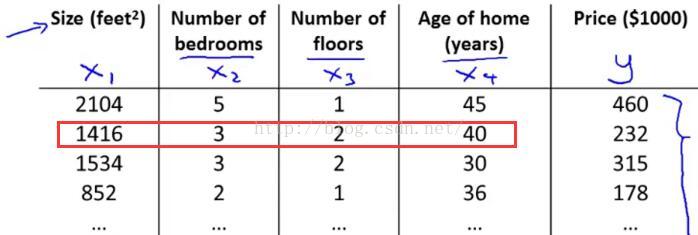
在之前學習過的線性回歸中,都是只有一個單一的特征量--房屋面積 x,如圖1-1所示,
圖1-1
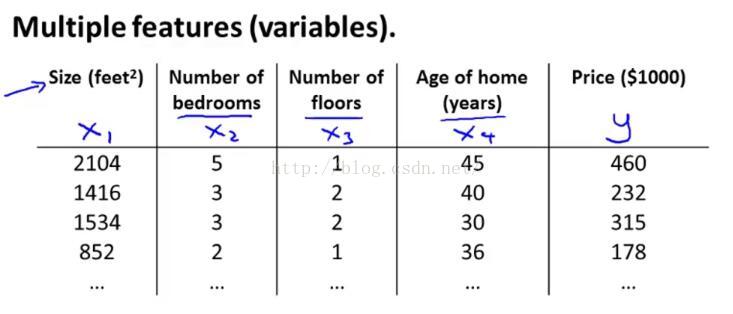
我們希望用房屋面積這個特征量來預測房子的價格。但是想象一下如果我們不僅有房屋面積作為預測房屋價格的特征量,我們還知道臥室的數量,樓層的數量以及房子的使用年限,如圖1-2所示,
圖1-2
這樣就給了我們更多可以用來預測房屋價格的信息了。接著我們先簡單介紹一下符號記法,一開始的時候就提到過我要用x1,x2,x3,x4來表示種情況下的四個特征量,然后仍然用 y來表示我們所想要預測的輸出變量 。除此之外,我們來看看更多的表示方式,如圖1-3
[第i個訓練樣本;第i個訓練樣本中第j個參數值]
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?圖1-3
?
首先介紹的是特征數量n,這里用小寫n來表示特征量的數目。因此在這個例子中,我們的n等于4(之前我們是用的“m”來表示樣本的數量,現在開始我們用n來表示特征量的數目)。
接著介紹的是第i個訓練樣本的輸入特征值x(i)(這里一定要看清是上標,不要搞混了)。舉個具體的例子來說x(2)就是表示第二個訓練樣本的特征向量,如圖1-4中用紅色框圈起來的位置,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖1-4
紅色框圈起來的這四個數字對應了我用來預測第二個房屋價格的四個特征量,因此在這種記法中,這個上標2就是訓練集的一個索引,而不是x的2次方,這個2就對應著你所看到的表格中的第二行,即我的第二個訓練樣本,同時也是一個四維向量。事實上更普遍
地來說這是n維的向量。
最后介紹的是第i個訓練樣本的第j個特征量,用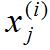
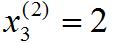
?
?
我們最初使用的假設函數只有一個唯一的特征量,如圖1-5黑色字體,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?圖1-5
但現在我們有了多個特征量,我們就不能再使用這種簡單的表示方式了。取而代之的我們將把線性回歸的假設改成圖1-5中藍色字體那樣。如果我們有n個特征量,那么我們要將所有的n個特征量相加,而不僅僅是四個特征量,如圖1-6所示。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖1-6
接下來,要做的是簡化這個等式的表示方式,為了表示方便我要將x0的(看清楚這里是下標)值設為1。具體而言,這意味著對于第i個樣本,都有一個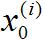
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?圖1-7
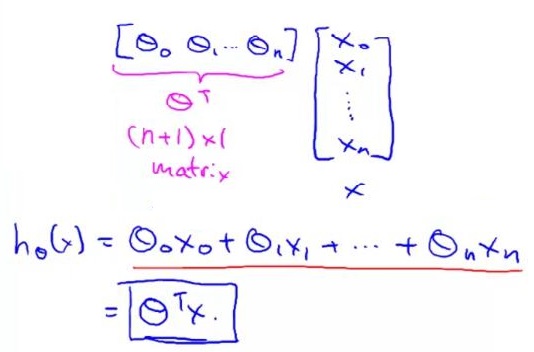
正是向量的引入,這里我們的假設函數可以換一種更加高效的方式來寫,如圖1-8,
圖1-8
這里我把假設函數等式寫成?θ轉置乘以X,這其實就是向量內積。這就為我們提供了一個表示假設函數更加便利的形式,即用參數向量θ以及特征向量X的內積。這樣的表示習慣就讓我們可以以這種緊湊的形式寫出假設。?
?
以上就是多特征量情況下的假設形式,另一個名字就是多元線性回歸。
?
二.Gradient Descent for Multiple Variables(多元線性回歸的梯度下降)
在之前我們談到的線性回歸的假設形式,是一種有多特征或者是多變量的形式。在這部分我們將會談到如何找到滿足這一假設的參數θ,尤其是如何使用梯度下降法來解決多特征的線性回歸問題。
現假設有多元線性回歸,并約定x0=1,該模型的參數是從θ0到θn,如圖2-1所示,
圖2-1
這里不要認為這是n+1個單獨的參數,我們要把這n+1個θ參數想象成一個n+1維的向量θ。
?
我們一開始的代價函數如圖2-2黑色字體所示,
圖2-2
但同樣地我們不要把函數J想成是一個關于n+1個自變量的函數,而是看成帶有一個n+1維向量的函數。
-----------------------------------------------------------------------------
關于圖2-2的這個公式要深入理解下,見圖2-3的練習
圖2-3
一開始選了2和4,提交后得知應該選擇1和2。分析如下:
選項1.其實這里的x(i)拆開后是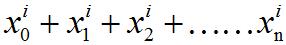
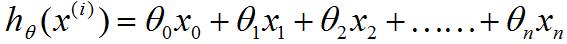
?
選項2.將括號里的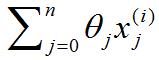
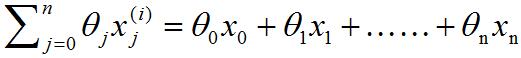
?
選項3.從1開始錯誤,我們規定了要從0開始。
?
選項4.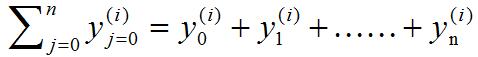
?
-----------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
https://www.cnblogs.com/ooon/p/4947688.html
1 問題的引出
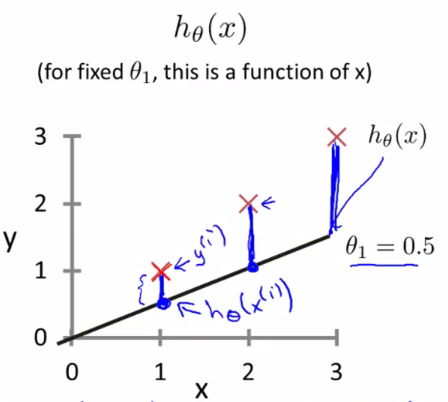
對于上篇中講到的線性回歸,先化一個為一個特征θ1,θ0為偏置項,最后列出的誤差函數如下圖所示:

手動求解
目標是優化J(θ1),得到其最小化,下圖中的×為y(i),下面給出TrainSet,{(1,1),(2,2),(3,3)}通過手動尋找來找到最優解,由圖可見當θ1取1時,![]() 與y(i)完全重合,J(θ1) = 0
與y(i)完全重合,J(θ1) = 0
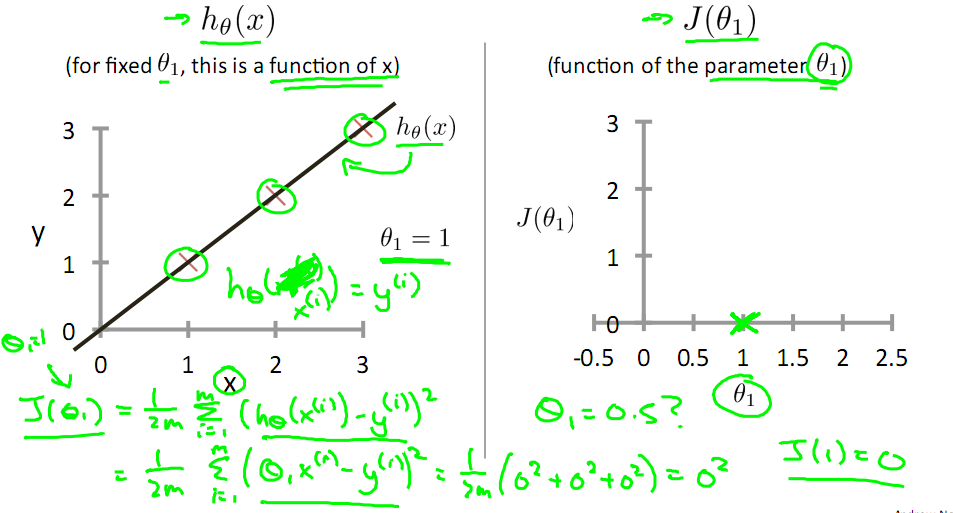
下面是θ1的取值與對應的J(θ1)變化情況
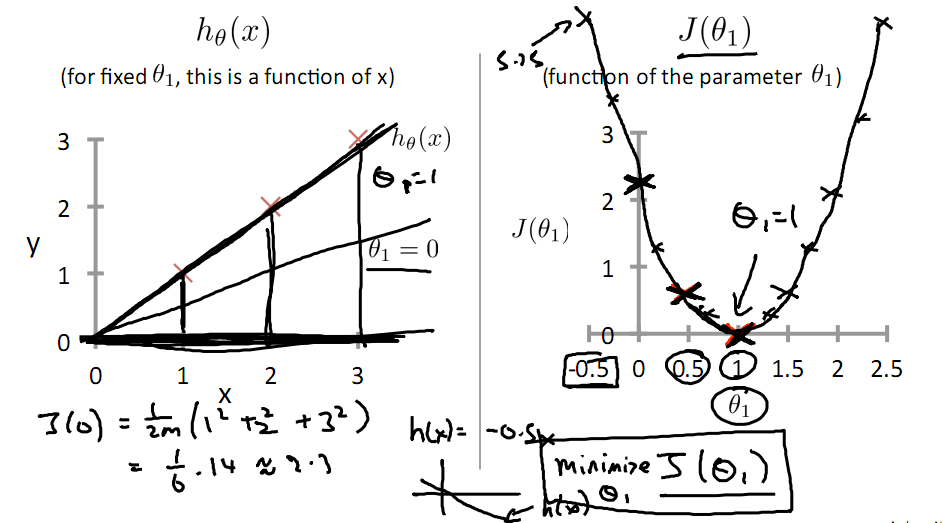
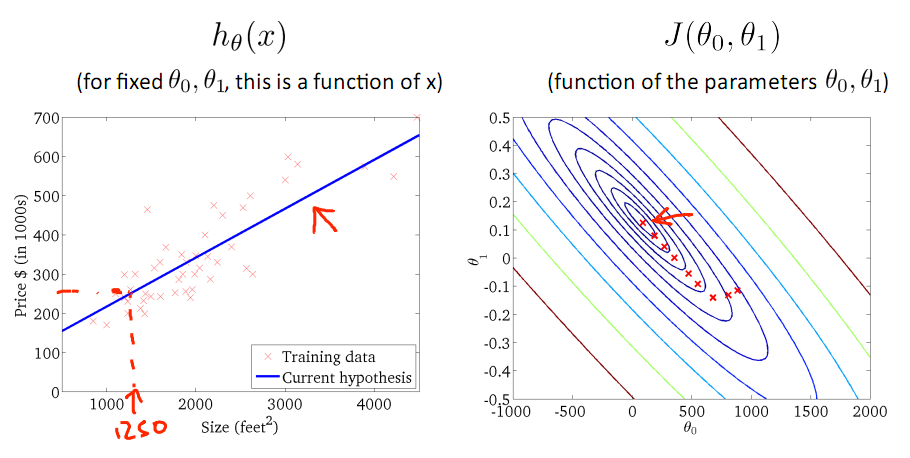
由此可見,最優解即為0,現在來看通過梯度下降法來自動找到最優解,對于上述待優化問題,下圖給出其三維圖像,可見要找到最優解,就要不斷向下探索,使得J(θ)最小即可。
2 梯度下降的幾何形式
下圖為梯度下降的目的,找到J(θ)的最小值。
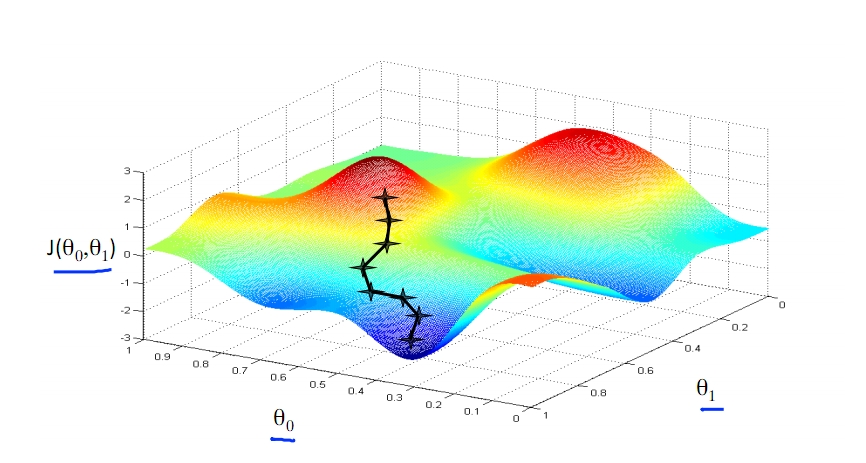
其實,J(θ)的真正圖形是類似下面這樣的,因為其是一個凸函數,只有一個全局最優解,所以不必擔心像上圖一樣找到局部最優解

直到了要找到圖形中的最小值之后,下面介紹自動求解最小值的辦法,這就是梯度下降法

對參數向量θ中的每個分量θj,迭代減去速率因子a* (dJ(θ)/dθj)即可,后邊一項為J(θ)關于θj的偏導數
3 梯度下降的原理
導數的概念
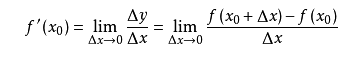
由公式可見,對點x0的導數反映了函數在點x0處的瞬時變化速率,或者叫在點x0處的斜度。推廣到多維函數中,就有了梯度的概念,梯度是一個向量組合,反映了多維圖形中變化速率最快的方向。
下圖展示了對單個特征θ1的直觀圖形,起始時導數為正,θ1減小后并以新的θ1為基點重新求導,一直迭代就會找到最小的θ1,若導數為負時,θ1的就會不斷增到,直到找到使損失函數最小的值。
?
?
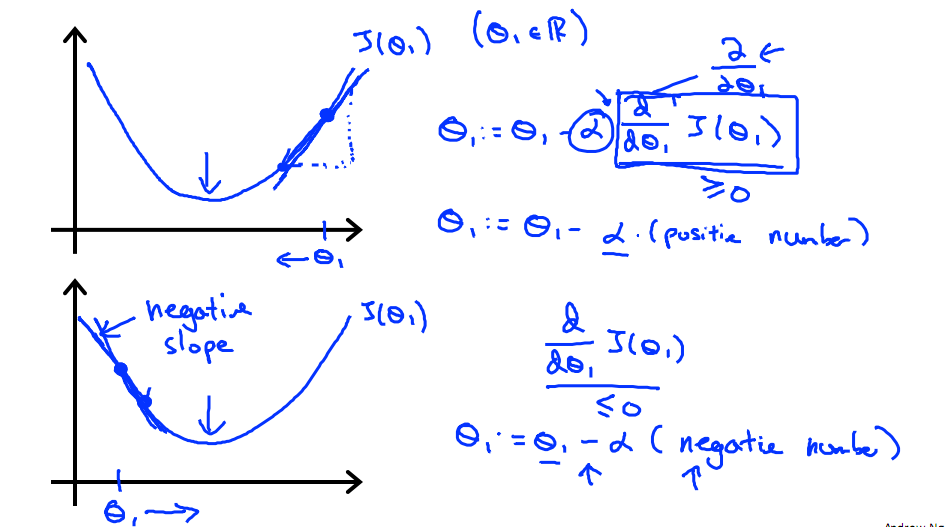
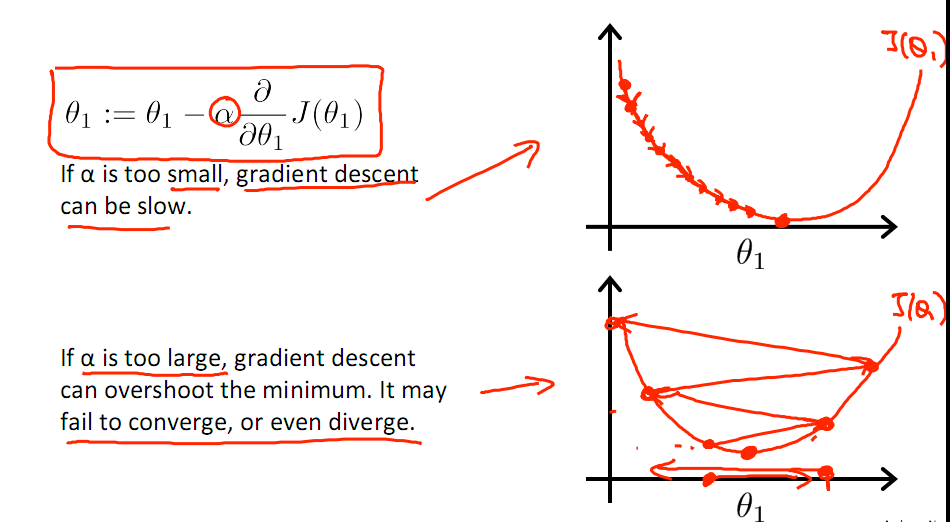
有一點需要注意的是步長a的大小,如果a太小,則會迭代很多次才找到最優解,若a太大,可能跳過最優,從而找不到最優解。
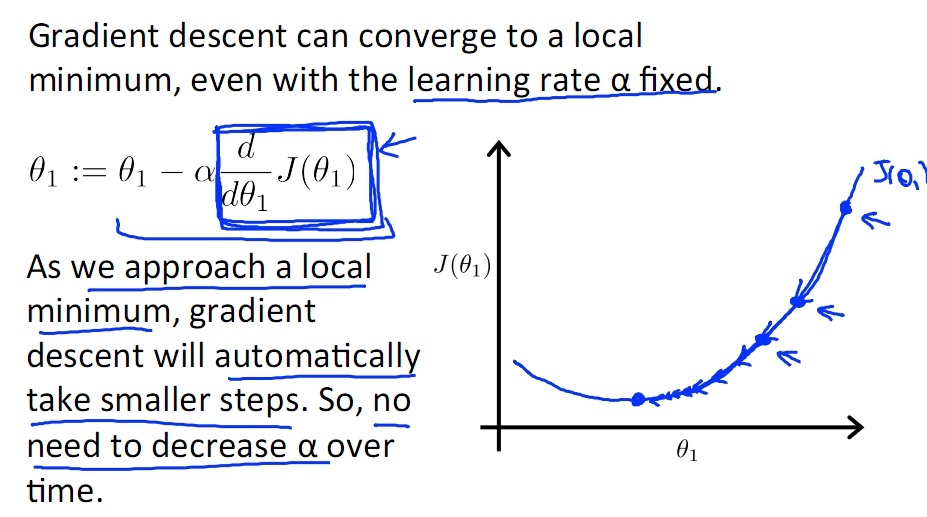
另外,在不斷迭代的過程中,梯度值會不斷變小,所以θ1的變化速度也會越來越慢,所以不需要使速率a的值越來越小
下圖就是尋找過程
當梯度下降到一定數值后,每次迭代的變化很小,這時可以設定一個閾值,只要變化小魚該閾值,就停止迭代,而得到的結果也近似于最優解。

若損失函數的值不斷變大,則有可能是步長速率a太大,導致算法不收斂,這時可適當調整a值
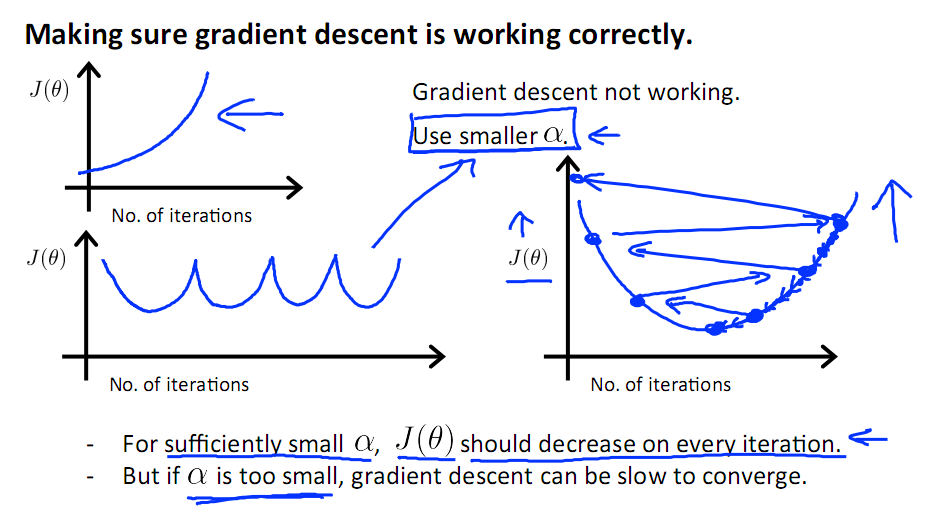
為了選擇參數a,就需要不斷測試,因為a太大太小都不太好。

?
?
如果想跳過的a與算法復雜的迭代,可以選擇 Normal Equation。
4 隨機梯度下降
對于樣本數量額非常之多的情況,Batch Gradient Descent算法會非常耗時,因為每次迭代都要便利所有樣本,可選用Stochastic Gradient Descent 算法,需要注意外層循環Loop,因為只遍歷一次樣本,不見得會收斂。

隨機梯度算法就可以用作在線學習了,但是注意隨機梯度的結果并非完全收斂,而是在收斂結果處波動的,可能由非線性可分的樣本引起來的:
可以有如下解決辦法:(來自MLIA)
1. 動態更改學習速率a的大小,可以增大或者減小
2. 隨機選樣本進行學習?
-----------------------------------------------------------------------------------------------------------------------------
講完代價函數,講梯度下降,如圖2-4所示,
圖2-4
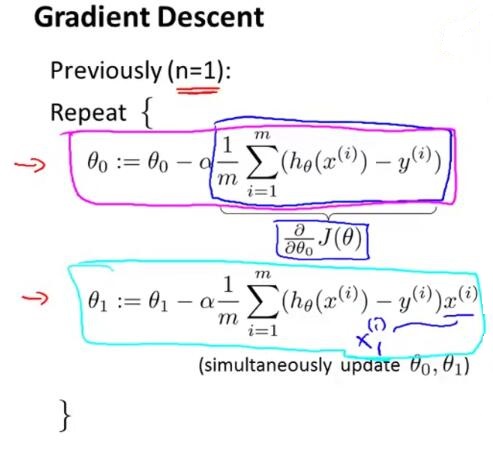
同理這里把函數J想成是帶有一個n+1維向量的函數。當我們實現梯度下降法后,我們可以仔細觀察一下它的偏導數項,圖2-5是我們當特征個數n=1時梯度下降的情況。我們有兩條針對參數θ0和θ1不同的更新規則,
圖2-5
圖2-5的兩個式子不同點在于對參數θ1我們有另一個更新規則,即在最后多了一項
X(i)。(http://blog.csdn.net/m399498400/article/details/52528722圖1-2中講解了這一項的推導過程)。
----------------------------推導過程------------------結合復合函數的求導(對什么參數求導,其他的參數就當做常數)--------
-----------------------------------------------------------------------------------------------------------------------------
以上是特征數量只有1個的情況下的梯度下降法的實現。當特征數量大于等于1個的時候,我們的梯度下降更新規則,變成了如圖2-6的形式。
圖2-6
其實圖2-5和圖2-6這兩種新舊算法實際上是一回事兒。考慮這樣一個情況,假設我們有3個特征數量,我們就會有對θ1、θ2、θ3的三條更新規則。如圖2-7所示,
圖2-7
仔細觀察θ0的更新規則,就會發現這跟之前圖2-5中n=1的情況是相同的。它們之所以是等價的是因為在我們的標記約定里有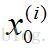
如果再仔細觀察θ1的更新規則,會發現這里的這一項是和圖2-5對參數θ1的更新項是等價的。在圖2-7中我們只是用了新的符號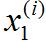
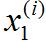
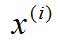
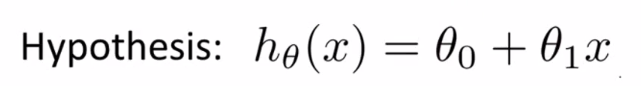
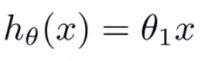
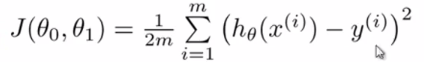

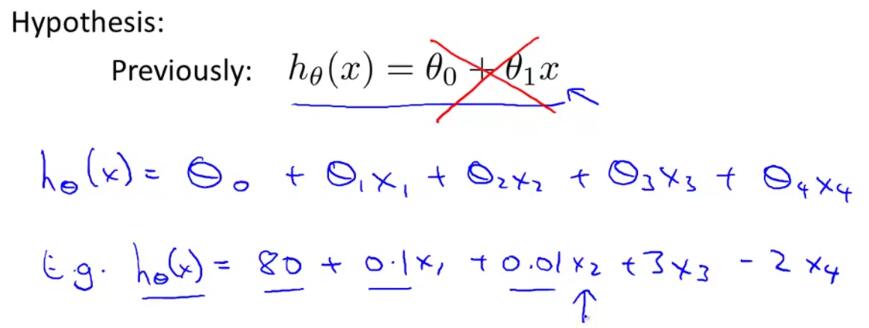
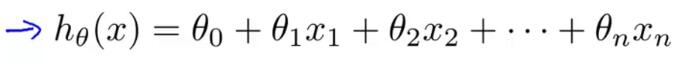

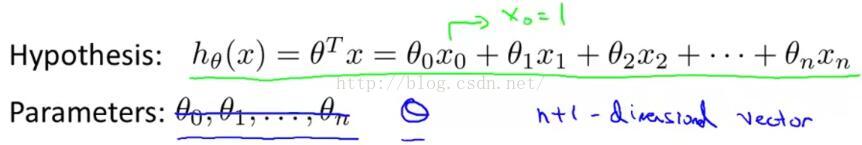
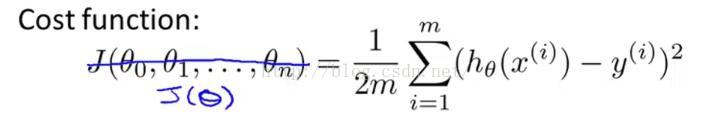












)












)