from：https://blog.csdn.net/gdut2015go/article/details/46779251
邊緣檢測是圖像處理和計算機視覺中的基本問題，邊緣檢測的目的是標識數字圖像中亮度變化明顯的點。圖像屬性中的顯著變化通常反映了屬性的重要事件和變化。這些包括：深度上的不連續、表面方向不連續、物質屬性變化和場景照明變化。 邊緣檢測是圖像處理和計算機視覺中，尤其是特征提取中的一個研究領域。圖像邊緣檢測大幅度地減少了數據量，并且剔除了可以認為不相關的信息，保留了圖像重要的結構屬性。有許多方法用于邊緣檢測，它們的絕大部分可以劃分為兩類：基于查找一類和基于零穿越的一類。基于查找的方法通過尋找圖像一階導數中的最大和最小值來檢測邊界，通常是將邊界定位在梯度最大的方向。基于零穿越的方法通過尋找圖像二階導數零穿越來尋找邊界，通常是Laplacian過零點或者非線性差分表示的過零點。
人類視覺系統認識目標的過程分為兩步:首先，把圖像邊緣與背景分離出來;然后，才能知覺到圖像的細節，辨認出圖像的輪廓。計算機視覺正是模仿人類視覺的這個過程。因此在檢測物體邊緣時，先對其輪廓點進行粗略檢測，然后通過鏈接規則把原來檢測到的輪廓點連接起來，同時也檢測和連接遺漏的邊界點及去除虛假的邊界點。圖像的邊緣是圖像的重要特征，是計算機視覺、模式識別等的基礎，因此邊緣檢測是圖象處理中一個重要的環節。然而，邊緣檢測又是圖象處理中的一個難題，由于實際景物圖像的邊緣往往是各種類型的邊緣及它們模糊化后結果的組合，且實際圖像信號存在著噪聲。噪聲和邊緣都屬于高頻信號，很難用頻帶做取舍。
這就需要邊緣檢測來進行解決的問題了。邊緣檢測的基本方法有很多：
一階的有Roberts Cross算子，Prewitt算子，Sobel算子，Canny算子，Krisch算子，羅盤算子；
二階的還有Marr-Hildreth，在梯度方向的二階導數過零點。現在就來簡單介紹一下各種算子的算法
Roberts算子
Roberts算子是一種利用局部差分算子尋找邊緣的算子，它有下式給出：
?
其中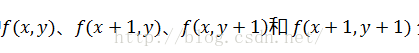
Roberts算子是2X2算子模板。圖1所示的2個卷積核形成了Roberts算子。圖象中的每一個點都用這2個核做卷積。
Sobel算子
Sobel算子是一種一階微分算子，它利用像素鄰近區域的梯度值來計算1個像素的梯度，然后根據一定的絕對值來取舍。它由下式給出:
Sobel算子是3*3算子模板。圖2所示的2個卷積核dx 、 dy形成Sobel算子。一個核對通常的垂直邊緣響應最大，而另一個核對水平邊緣響應最大。2個卷積的最大值作為該點的輸出值。運算結果是一幅邊緣幅度圖像。
Prewitt算子
Prewitt算子由下式給出：
Prewitt算子是3*3算子模板。圖3所示的2個卷積核dx ,不要形成了Prewitt算子。與Sobel算子的方法一樣，圖像中的每個點都用這2個核進行卷積，取最大值作為輸出值。Prewitt算子也產生一幅邊緣幅度圖像。
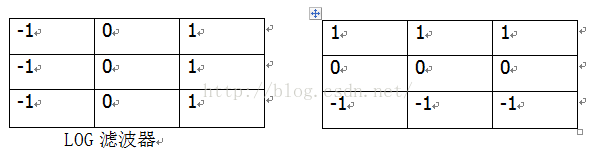
LOG濾波器又稱Marr-Hildreth模板或算子
式中：G(x,y)是對圖像進行處理時選用的平滑函數(Gaussian函數);x，y為整數坐標; σ為高斯分布的均方差。對平滑后的圖像fs(fs=f(x,y)*G(x,y))做拉普拉斯變換，得：
即先對圖象平滑，后拉氏變換求二階微分，等效于把拉氏變化作用于平滑函數，得到1個兼有平滑和二階微分作用的模板，再與原來的圖像進行卷積。用Marr-Hildreth模板與圖像進行卷積的優點在于，模板可以預先算出，實際計算可以只進行卷積。
LOG濾波器有以下特點:
(1)通過圖象平滑，消除了一切尺度小于σ的圖像強度變化;
(2)若用其它微分法，需要計算不同方向的微分，而它無方向性，因此可以節省計算量;
(3)它定位精度高，邊緣連續性好，可以提取對比度較弱的邊緣點。
LOG濾波器也有它的缺點:當邊緣的寬度小于算子寬度時，由于過零點的斜坡融合將會丟失細節。
LOG濾波器有無限長的拖尾，若取得很大尺寸，將使得計算不堪重負。但隨著: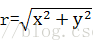
當σ1/σ2=1.6時，DOG代替LOG減少了計算量。
Canny算子
Canny算子是是一階算子。其方法的實質是用1個準高斯函數作平滑運算fs=f(x,y)*G(x,y),然后以帶方向的一階微分算子定位導數最大值。
??? ?平滑后fs(x，y)的梯度可以使用2*2的一階有限差分近似式:
P[i,j]≈(fs[i,j+1]-fs[i,j]+fs[i+1,j+1]-fs[i+1,j])/2
Q[i,j]≈(fs[i,j]-fs[i+1,j]+fs[i,j+1]-fs[i+1,j+1])/2
在這個2x2正方形內求有限差分的均值，便于在圖像中的同一點計算二和y的偏導數梯度。幅值和方向角可用直角坐標到極坐標的坐標轉化來計算:
?
M[i,j]反映了圖象的邊緣強度;反映了邊緣的方向。使得M}i,j}取得局部最大值的方向角，就反映了邊緣的方向。
Canny算子也可用高斯函數的梯度來近似，在理論上很接近4個指數函數的線性組合形成的最佳邊緣算子。在實際工作應用中編程較為復雜且運算較慢。
幾種算子的比較
Robert算子定位比較精確，但由于不包括平滑，所以對于噪聲比較敏感；
Prewitt算子和Sobel算子都是一階的微分算子，而前者是平均濾波，后者是加權平均濾波且檢測的圖像邊緣可能大于2個像素。這兩者對灰度漸變低噪聲的圖像有較好的檢測效果，但是對于混合多復雜噪聲的圖像，處理效果就不理想了。；
LOG濾波器方法通過檢測二階導數過零點來判斷邊緣點。LOG濾波器中的a正比于低通濾波器的寬度，a越大，平滑作用越顯著，去除噪聲越好，但圖像的細節也損失越大，邊緣精度也就越低。所以在邊緣定位精度和消除噪聲級間存在著矛盾，應該根據具體問題對噪聲水平和邊緣點定位精度要求適當選取。
討論和比較了幾種常用的邊緣檢測算子。梯度算子計算簡單,但精度不高,只能檢測出圖像大致的輪廓,而對于比較細的邊緣可能會忽略。Prewitt 和Sobel 算子比Roberts 效果要好一些。LOG 濾波器和Canny 算子的檢測效果優于梯度算子,能夠檢測出圖像較細的邊緣部分。不同的系統,針對不同的環境條件和要求,選擇合適的算子來對圖像進行邊緣檢測。
---------------------------------------------------------------------------------------------------------------------------------------------
from：https://blog.csdn.net/xiaojiegege123456/article/details/7714863
不同圖像灰度不同，邊界處一般會有明顯的邊緣，利用此特征可以分割圖像。需要說明的是：邊緣和物體間的邊界并不等同，邊緣指的是圖像中像素的值有突變的地方，而物體間的邊界指的是現實場景中的存在于物體之間的邊界。有可能有邊緣的地方并非邊界，也有可能邊界的地方并無邊緣，因為現實世界中的物體是三維的，而圖像只具有二維信息，從三維到二維的投影成像不可避免的會丟失一部分信息；另外，成像過程中的光照和噪聲也是不可避免的重要因素。正是因為這些原因，基于邊緣的圖像分割仍然是當前圖像研究中的世界級難題，目前研究者正在試圖在邊緣提取中加入高層的語義信息。
在實際的圖像分割中，往往只用到一階和二階導數，雖然，原理上，可以用更高階的導數，但是，因為噪聲的影響，在純粹二階的導數操作中就會出現對噪聲的敏感現象，三階以上的導數信息往往失去了應用價值。二階導數還可以說明灰度突變的類型。在有些情況下，如灰度變化均勻的圖像，只利用一階導數可能找不到邊界，此時二階導數就能提供很有用的信息。二階導數對噪聲也比較敏感，解決的方法是先對圖像進行平滑濾波，消除部分噪聲，再進行邊緣檢測。不過，利用二階導數信息的算法是基于過零檢測的，因此得到的邊緣點數比較少，有利于后繼的處理和識別工作。
各種算子的存在就是對這種導數分割原理進行的實例化計算，是為了在計算過程中直接使用的一種計算單位；
Roberts算子：邊緣定位準，但是對噪聲敏感。適用于邊緣明顯且噪聲較少的圖像分割。Roberts邊緣檢測算子是一種利用局部差分算子尋找邊緣的算子,Robert算子圖像處理后結果邊緣不是很平滑。經分析，由于Robert算子通常會在圖像邊緣附近的區域內產生較寬的響應，故采用上述算子檢測的邊緣圖像常需做細化處理，邊緣定位的精度不是很高。
Prewitt算子：對噪聲有抑制作用，抑制噪聲的原理是通過像素平均，但是像素平均相當于對圖像的低通濾波，所以Prewitt算子對邊緣的定位不如Roberts算子。
Sobel算子：Sobel算子和Prewitt算子都是加權平均，但是Sobel算子認為，鄰域的像素對當前像素產生的影響不是等價的，所以距離不同的像素具有不同的權值，對算子結果產生的影響也不同。一般來說，距離越遠，產生的影響越小。
Isotropic Sobel算子：加權平均算子，權值反比于鄰點與中心點的距離，當沿不同方向檢測邊緣時梯度幅度一致，就是通常所說的各向同性。
在邊沿檢測中，常用的一種模板是Sobel?算子。Sobel 算子有兩個，一個是檢測水平邊沿的；另一個是檢測垂直平邊沿的 。Sobel算子另一種形式是各向同性Sobel(Isotropic Sobel)算子，也有兩個，一個是檢測水平邊沿的，另一個是檢測垂直平邊沿的 。各向同性Sobel算子和普通Sobel算子相比，它的位置加權系數更為準確，在檢測不同方向的邊沿時梯度的幅度一致。由于建筑物圖像的特殊性，我們可以發現，處理該類型圖像輪廓時，并不需要對梯度方向進行運算，所以程序并沒有給出各向同性Sobel算子的處理方法。
? ??由于Sobel算子是濾波算子的形式，用于提取邊緣，可以利用快速卷積函數，簡單有效，因此應用廣泛。美中不足的是，Sobel算子并沒有將圖像的主體與背景嚴格地區分開來，換言之就是Sobel算子沒有基于圖像灰度進行處理，由于Sobel算子沒有嚴格地模擬人的視覺生理特征，所以提取的圖像輪廓有時并不能令人滿意。??在觀測一幅圖像的時候，我們往往首先注意的是圖像與背景不同的部分，正是這個部分將主體突出顯示，基于該理論，我們可以給出閾值化輪廓提取算法，該算法已在數學上證明當像素點滿足正態分布時所求解是最優的。
上面的算子是利用一階導數的信息，屬于梯度算子范疇。
Laplacian算子：這是二階微分算子。其具有各向同性，即與坐標軸方向無關，坐標軸旋轉后梯度結果不變。但是，其對噪聲比較敏感，所以，圖像一般先經過平滑處理，因為平滑處理也是用模板進行的，所以，通常的分割算法都是把Laplacian算子和平滑算子結合起來生成一個新的模板。
Laplacian算子一般不以其原始形式用于邊緣檢測，因為其作為一個二階導數，Laplacian算子對噪聲具有無法接受的敏感性；同時其幅值產生算邊緣，這是復雜的分割不希望有的結果；最后Laplacian算子不能檢測邊緣的方向；所以Laplacian在分割中所起的作用包括：（1）利用它的零交叉性質進行邊緣定位；（2）確定一個像素是在一條邊緣暗的一面還是亮的一面；一般使用的是高斯型拉普拉斯算子（Laplacian of a Gaussian,LoG)，由于二階導數是線性運算，利用LoG卷積一幅圖像與首先使用高斯型平滑函數卷積改圖像，然后計算所得結果的拉普拉斯是一樣的。所以在LoG公式中使用高斯函數的目的就是對圖像進行平滑處理，使用Laplacian算子的目的是提供一幅用零交叉確定邊緣位置的圖像；圖像的平滑處理減少了噪聲的影響并且它的主要作用還是抵消由Laplacian算子的二階導數引起的逐漸增加的噪聲影響。
?
幾種常用的邊緣檢測算子主要有Roberts邊緣檢測算子，Sobel算子、Prewitt算子、Krisch邊緣算子，高斯-拉普拉斯算子。
邊緣大致可以分為兩種，一種是階躍狀邊緣，邊緣兩邊像素的灰度值明顯不同；另一種為屋頂狀邊緣，邊緣處于灰度值由小到大再到小的變化轉折點處。
邊緣檢測的主要工具是邊緣檢測模板。我們以一個一維模板為例來考察邊緣檢測模板是如何作用的。假設有一個模板
?和一幅圖象
可以看出，圖象中左邊暗，右邊亮，中間存在著一條明顯的邊緣，是一個典型階躍狀邊緣。使用模板?進行模板操作后，結果如下
可以看出，邊緣檢測后的圖象在原圖象暗亮邊緣處的灰度值高很多。觀察時，就能發現一條很明顯的亮邊，其他區域都很暗，這樣就起到了邊緣檢測的作用。
模板的作用是將右鄰點的灰度值減去左鄰點的灰度值作為該點的灰度值。在灰度相近的區域內，這么做的結果使得該點的灰度值接近于0；而在邊緣附近，灰度值有明顯的跳變，這么做的結果使得該點的灰度值很大，這樣就出現了上面的結果。這種模板就是一種邊緣檢測器，它在數學上的涵義是一種基于梯度的濾波器，習慣上又稱邊緣算子。我們知道，梯度是有方向的，和邊緣的方向總是垂直的。模板是水平方向的，而上面那幅圖象的邊緣恰好是垂直方向的，使用模板就可以將它檢測出來。如果圖象的邊緣是水平方向的，我們可以用梯度是垂直
方向的模板?檢測它的邊緣。如果圖象的邊緣是45。方向的，我們可以用模板
?檢測它的邊緣。
常用的邊緣檢測模板有Laplacian算子、Roberts算子、Sobel算子、log（Laplacian-Gauss）算子、Kirsch算子和Prewitt算子等。
?
二.Roberts算子
?
如果我們沿如下圖方向角度求其交叉方向的偏導數，則得到Roberts于1963年提出的交叉算子邊緣檢測方法。該方法最大優點是計算量小，速度快。但該方法由于是采用偶數模板，如下圖所示，所求的(x,y)點處梯度幅度值，其實是圖中交叉點處的值，從而導致在圖像(x,y)點所求的梯度幅度值偏移了半個像素（見下圖）。
?
?
Roberts算子的推導：
?
Sobel算子
?
Sobel算子也有兩個，一個是檢測水平邊緣的模板
?，另一個是檢測水平邊緣的模板
?。與Prewitt算子相比，Sobel算子對于象素位置的影響作了加權，因此效果更好。
sobel算子的另一種形式是各向同性Sobel算子，也有兩個模板組成，一個是檢測水平邊緣的
?，另一個是檢測垂直邊緣的
。各向同性Sobel算子和普通Sobel算子相比，位置加權系數更為準確，在檢測不同方向的邊緣時梯度的幅度一致。
Sobel算子的推導：
Prewitt算子
Prewitt算子由兩部分組成，檢測水平邊緣的模板
?和
檢測垂直邊緣的模板
prewitt算子一個方向求微分，一個方向求平均，所以對噪聲相對不敏感。
?
laplacian算子
Laplacian算子定義為
它的差分形式為
表示成模板的形式就是?
。Laplacian算子另外一種形式是
，也經常使用。Laplace算子是一種各向同性算子，在只關心邊緣的位置而不考慮其周圍的象素灰度差值時比較合適。Laplace算子對孤立象素的響應要比對邊緣或線的響應要更強烈，因此只適用于無噪聲圖象。存在噪聲情況下，使用Laplacian算子檢測邊緣之前需要先進行低通濾波。
)
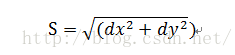
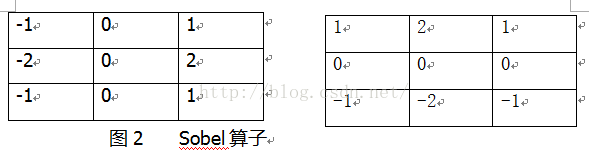
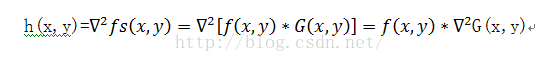
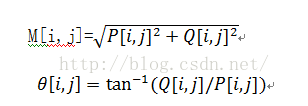
