from:https://blog.csdn.net/zhi_neng_zhi_fu/article/details/51029864
模板匹配(Template Matching)算法
模板匹配(Template Matching)是圖像識別中最具代表性的方法之一。它從待識別圖像中提取若干特征向量與模板對應的特征向量進行比較,計算圖像與模板特征向量之間的距離,用最小距離法判定所屬類別。模板匹配通常事先建立好標準模板庫。
一、簡單計算樣本之間距離的方法
在工作過程中遇到一個判斷樣本距離的方法,先把他記錄如下:?
循環計算待測樣本和訓練集中已知樣本之間的距離,比較所有的距離值,找出與待測樣本最近的已知樣品,其中所對應的樣本所屬的類別就是待測樣本X所屬的類別。
c實現代碼如下:
<span style="color:#000000"><code>/****************************************
*參數:
* src:待匹配特征向量
* template:模板向量
*返回值:
* int:返回匹配結果;-1:無匹配項
*意義:
* 輸入待匹配特征向量,輸出匹配結果*****************************************/
#define NFeature 25 //特征個數
#define NSample 10 //樣本個數
int templateMatching(double src[], double template[][NFeature])
{double d[11] = {0.0}, temp, mind = 10.0; //匹配度int flag = -1, i, j;for(j = 0; j < NSample; j++) {for(i = 0; i < NFeature; i++) {temp = pow(src[i] - template[j][i], 2);d[j] += temp;}d[j] = sqrt(d[j]);if(mind > d[j]) {mind = d[j];flag = j; }}return flag;
}
</code></span>不足之處
以上算法有一個很大的問題,就是當特征向量值順序改變之后,計算結果有很大的變化。例如:?
B = {1, 2, 3, 4}; A1 = {4, 3, 2, 1}; A2 = {1,2,3,4}。A1與B匹配,結果為{3*3+1*1+1*1+3*3} = 20;A2與B匹配,結果為{0+0+0+0} = 0;很明顯特征向量A1與A2是相同的,在實際圖像識別過程中有可能造成:一個圖像旋轉了一定角度,就無法識別出來。所以,這個算法只適合同方向的物體匹配,例如車牌字符識別等。
總結:
1. 只適合恒定方向特征匹配,例如車牌中的字符特征匹配
二、Hausdorff距離匹配
Hausdorff是描述兩組點之間相似程度的一種度量,它是集合和集合之間距離的一種定義形式。下面我們慢慢講解Hausdorff算法的過程。
- 點到點集的距離

- A集合到B集合的直接Hausdorff距離

還是以上面的例子為例來說明。例如:B = {1, 2, 3, 4}, A1 = {4, 3, 2, 1}, A2 = {1 ,2, 3, 4};A1與B匹配:Max{0, 0} = 0; A2與B的匹配:Max{0, 0} = 0;可以看到匹配的結果是:A1與A2是相同的,即使他們特征元素的順序打亂了。一樣可以把他們都正確匹配出來。?
如圖所示,X1、X2與T是一樣的特征向量,只是順序打亂了,但是匹配都是0;匹配效果還是很好的。X3是隨機生成的其他的特征向量。?
代碼:
下面按照最一般的情況,計算待測特征向量X與某一樣本T的匹配度。特征元素為有理數。
<span style="color:#000000"><code>/********************************************************參數:X:輸入特征向量數組T:模板庫中某一樣本特征向量n: 特征向量個數返回值:返回匹配結果函數意義:通過輸入待測特征向量和模板特征向量,計算出待測特征向量的匹配度,數值越小,匹配程度越高。式中的距離范式是特征元素之間的差值絕對值。 ***************************************************/
double charrecognize(double X[], double T[], int n)
{int i,j;double d[2] = {0.0};//存儲X-->T的Hausdorff和T-->X的Hausdorff值double minTemp = 1000.0, sum;//計算X-->T的Hausdoff值for(i = 0; i < n; i++) {minTemp = 1000.0;for(j = 0; j < n; j++) {sum = fabs(X[i] - T[j]);if(sum < minTemp)minTemp = sum; }d[0] += minTemp; }//計算T-->X的Hausdorff值for(j = 0; j < n; j++) {minTemp = 1000.0;for(i = 0; i < n; i++) {sum = fabs(T[j] - X[i]);if(sum < minTemp)minTemp = sum;}d[1] += minTemp; }//返回較大值if(d[0] > d[1])return d[0];return d[1];
}
</code></span>當我們匹配要求特定方向、特定位置的圖片時,其實也可以用Hausdorff距離進行特征匹配。?
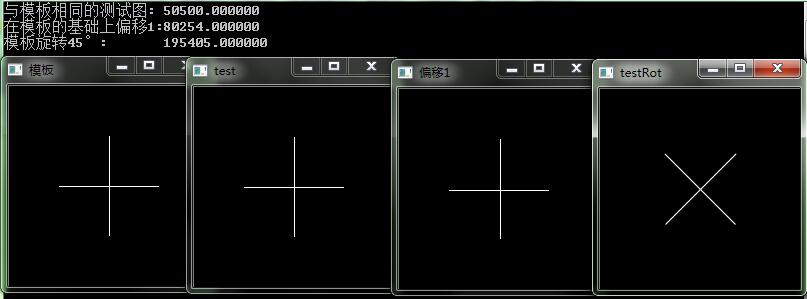
如圖所示,第一幅圖是模板圖片,后面都是要與模板進行匹配的圖像。
- 第一幅圖像是模板的copy,計算出的數值為:50500.
- 第二幅圖像在模板的基礎之上進行向左向右移動了一個像素:80254.
- 第三幅圖像是把模板旋轉了45°,計算出來的結果是:195405.
三幅圖像雖然是一樣的,只是位置和角度偏移了一些,出現的結果偏差卻很大。這并非說明Hausdorff距離算法性能不佳,只是上述實驗中的“特征選擇”限定了Hausdorff距離算法對偏移和旋轉過于敏感,也正是因為有了這種敏感,也更容易區分“非匹配項”。當我們圖像特征限定在某一方向和位置時,Hausdorff將表現出優異的區分性能。例如:字符模板限定在“字符重心在圖片重心,不旋轉”,待測樣本也如此限定。
代碼流程
- 待測樣本為二值化特征向量X, 模板為二值化特征向量T;
- 從上到下,從左到右,逐個像素掃描樣本。如果為255(特征點),記錄坐標P(x, y);如果為0,跳過。
- 在模板上,以P(x, y)為中心的3*3的鄰域內,搜索255(特征點),尋找與P(x, y)最近的點,并計算最近距離;如果3*3域內沒有255(特征點),就認為距離為一個設定的較大點(例如:5.0)。
- 把所有計算的距離累加到樣本至模板的距離D(X, T);
- 以同樣的方法計算模板至樣本的距離D(T, D);
-
取D = Max{D(X, T), D(T, X)},作為匹配的結果。
<span style="color:#000000"><code>/**************************************** 參數:X:樣本二值圖,只包含特征信息T:模板二值圖,只包含特征信息 返回值:double:返回匹配度,越低越匹配 意義:以樣本二值圖特征像素坐標作為特征點進行 匹配。 *****************************************/ double charrecognise(Mat X, Mat T) {int i, j, m, n;double distemp = 5.0, distemp1, distsum, distsum1;//樣本到模板的距離distsum = 0.0;for(i = 0; i < X.cols; i++) {for(j = 0; j < X.rows; j++) {if(X.at<uchar>(i, j) == 255) {distemp = 5.0;for(m = i - 3; m <= i + 3; m++) {for(n = j - 3; n <= j + 3; n++) {if(m < 0) m = 0;if(m > X.cols) m = X.cols;if(n < 0) n = 0;if(n > X.rows) n = X.rows;if(T.at<uchar>(m, n) == 255) {distemp1 = sqrt(pow((double)m - i, 2) + pow((double)n - j, 2));if(distemp1 < distemp) distemp = distemp1;}}}}distsum += distemp;}}//模板到樣本的距離distsum1 = 0.0;for(i = 0; i < T.cols; i++) {for(j = 0; j < T.rows; j++) {if(T.at<uchar>(i, j) == 255) {distemp = 5.0;for(m = i - 3; m <= i + 3; m++) {for(n = j - 3; n <= j + 3; n++) {if(m < 0) m = 0;if(m > T.cols) m = T.cols;if(n < 0) n = 0;if(n > T.rows) n = T.rows;if(X.at<uchar>(m, n) == 255) {distemp1 = sqrt(pow((double)m - i, 2) + pow((double)n - j, 2));if(distemp1 < distemp) distemp = distemp1;}}}distsum1 += distemp;}}}if(distsum > distsum1)return distsum;return distsum1; } </code></span>
總結
- Hausdorff距離算法能無視特征元素的順序進行匹配。
- Hausdorff距離算法對以位置為特征元素的特征向量進行匹配時,效果很差,但是對匹配條件加以限定還是可以達到很好的區分效果。



)












)


