from：https://blog.csdn.net/linear_luo/article/details/52576082

1 經典ICP

　　ICP的目的很簡單，就是求解兩堆點云之間的變換關系。怎么做呢？思路很自然，既然不知道R和t(針對剛體運動)，那我們就假設為未知量唄，然后通過某些方法求解。下面我們來看看具體怎么求的～沒辦法，要把問題描述清楚，數學是少不了的了。假設有兩堆點云，分別記為兩個集合X=x1,x2,...,xmX=x1,x2,...,xm和Y=y1,y2,...,ymY=y1,y2,...,ym（m并不總是等于n）。然后呢，我們不失一般性的，假設兩個點云之間的變換為R（旋轉變換）和t（平移變換），這兩個就是我們要求的東西啦～那我們將求解這個問題描述成最小化均方誤差：?
　　

e(X,Y)=∑i=1m(Rxi+t?yi)2e(X,Y)=∑i=1m(Rxi+t?yi)2

　　經典的ICP方法對上面的優化問題的處理思路如下：?
　　（1）初始化RR?和?tt?
　　確定初始的RR?和?tt?的方法很多，如果什么方法都不知道，那隨便賦一個RR?和?tt?，然后就迭代的算呀。隨便給一個值從原理上來說也可以得到最終的一個結果呀，但是準不準就不知道了。相信有基本的優化概念的人都知道，初始值的選取很重要，如果初始值選的不好很容易收斂到一個局部最優解，然后局部最優解好不好那就另說了。ICP發展了這么多年了，當然有很多的方法來估計初始的R和t了，像PCL給的SampleConsensusInitalAlignment函數以及TransformationEstimationSVD函數都可以得到較好的初始估計。?
　　（2）迭代?
　　得到初始的估計后，接下來的步驟就順理成章了：對于XX中的每一個點用當前的RR?和?tt在YY中找最近的點（比如用歐式距離），然后這兩個點就成了一對了～就這樣，對所有的點都這么做一次，然后我們就得到了所有的匹配對了～然后呢，用每一對的坐標列一個方程，就得到一系列的方程。然后就求解最優的R和t最小化上面的誤差。如此循環往復。

?

2 ICP變種

　　除了經典的ICP方法外，還有一些變種，如point-to-point的，point-to-plane的以及plane-to-plane的，那么這三種方法到底是啥呢？?
　　其實很簡單，就是上面的誤差函數的定義不一樣而已。在上面講經典ICP的時候，求和的每一項不就是XX中的每一個點到YY中的每一個點的距離嗎？那就是point-to-point了，那么將求和的每一項變成XX中的每一個點到YY中的平面的距離，那就是point-to-plane了呀～類似的，如果把求和的每一項變成X中的平面到YY中的平面的距離，那就是plane-to-plane了。我們說了這么久的平面，那么平面到時是怎么定義的呢？?
　　point-to-plane的誤差函數定義為：Mopt=argminR,t∑i((R?xi+t?yi)?ni)Mopt=argminR,t∑i((R?xi+t?yi)?ni)

參考：http://www.cnblogs.com/jian-li/articles/4945676.html

-------------------------------------------------------------------------------------------------------------------------------------------

　圖像配準是圖像處理研究領域中的一個典型問題和技術難點，其目的在于比較或融合針對同一對象在不同條件下獲取的圖像，例如圖像會來自不同的采集設備，取自不同的時間，不同的拍攝視角等等，有時也需要用到針對不同對象的圖像配準問題。具體地說，對于一組圖像數據集中的兩幅圖像，通過尋找一種空間變換把一幅圖像映射到另一幅圖像，使得兩圖中對應于空間同一位置的點一一對應起來，從而達到信息融合的目的。?一個經典的應用是場景的重建，比如說一張茶幾上擺了很多杯具，用深度攝像機進行場景的掃描，通常不可能通過一次采集就將場景中的物體全部掃描完成，只能是獲取場景不同角度的點云，然后將這些點云融合在一起，獲得一個完整的場景。

　　ICP（Iterative Closest Point迭代最近點）算法是一種點集對點集配準方法。如下圖所示，PR（紅色點云）和RB（藍色點云）是兩個點集，該算法就是計算怎么把PB平移旋轉，使PB和PR盡量重疊。

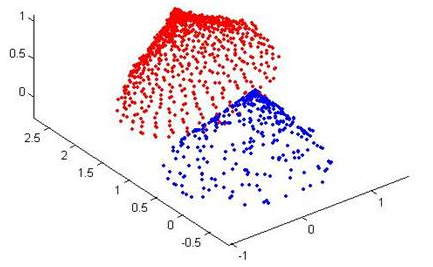
　　用數學語言描述如下，即ICP算法的實質是基于最小二乘法的最優匹配，它重復進行“確定對應關系的點集→計算最優剛體變換”的過程，直到某個表示正確匹配的收斂準則得到滿足。

ICP算法基本思想：

　　如果知道正確的點對應，那么兩個點集之間的相對變換（旋轉、平移）就可以求得封閉解。

　　首先計算兩個點集X和P的質心，分別為μx和μp

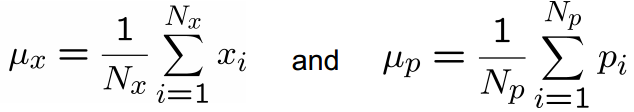
　　然后在兩個點集中分別減去對應的質心（Subtract the corresponding center of mass?from every point in the two point sets?before calculating the transformation）

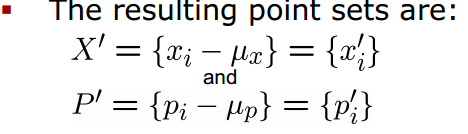
　　目標函數E(R,t)的優化是ICP算法的最后一個階段。在求得目標函數后，采用什么樣的方法來使其收斂到最小，也是一個比較重要的問題。求解方法有基于奇異值分解的方法、四元數方法等。?

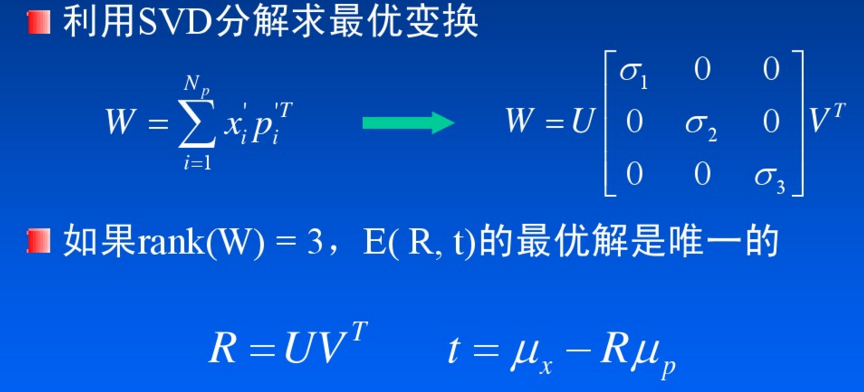
　　如果初始點“足夠近”，可以保證收斂性

ICP算法優點：

• 可以獲得非常精確的配準效果
• 不必對處理的點集進行分割和特征提取
• 在較好的初值情況下，可以得到很好的算法收斂性

ICP算法的不足之處：?

• 在搜索對應點的過程中，計算量非常大，這是傳統ICP算法的瓶頸
• 標準ICP算法中尋找對應點時，認為歐氏距離最近的點就是對應點。這種假設有不合理之處，會產生一定數量的錯誤對應點

　　針對標準ICP算法的不足之處，許多研究者提出ICP算法的各種改進版本，主要涉及如下所示的6個方面。

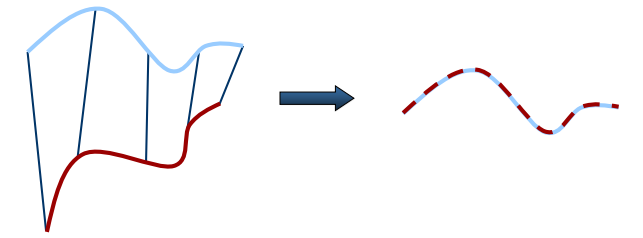
　　標準ICP算法中，選用點集中所有的點來計算對應點，通常用于配準的點集元素數量都是非常巨大的，通過這些點集來計算，所消耗的時間很長。在后來的研究中，提出了各種方法來選擇配準元素，這些方法的主要目的都是為了減小點集元素的數目，即如何選用最少的點來表征原始點集的全部特征信息。在點集選取時可以：1.選取所有點；2.均勻采樣（Uniform sub-sampling?）；3.隨機采樣（Random sampling）；4.按特征采樣（Feature based Sampling ）；5.法向空間均勻采樣（Normal-space sampling），如下圖所示，法向采樣保證了法向上的連續性（Ensure that samples have normals distributed as?uniformly as possible）

　　基于特征的采樣使用一些具有明顯特征的點集來進行配準，大量減少了對應點的數目。

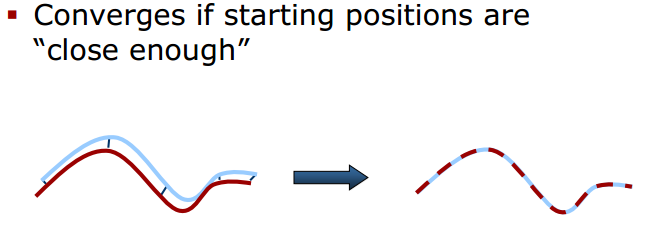
　　點集匹配上有：最近鄰點（Closet Point）

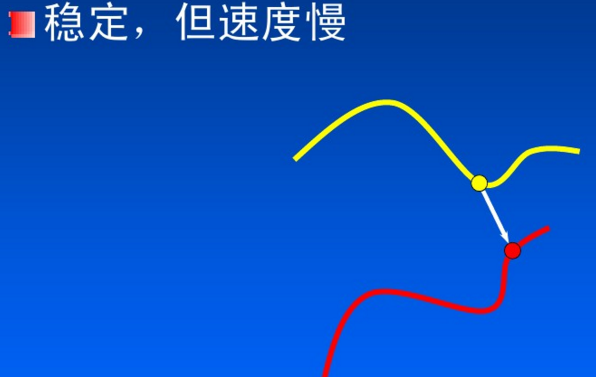　　法方向最近鄰點（Normal Shooting）

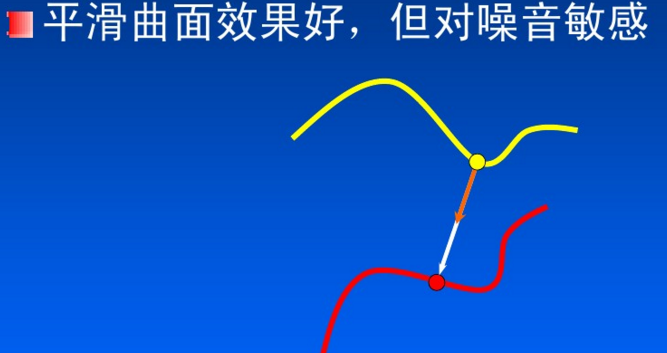
　　投影法（Projection）
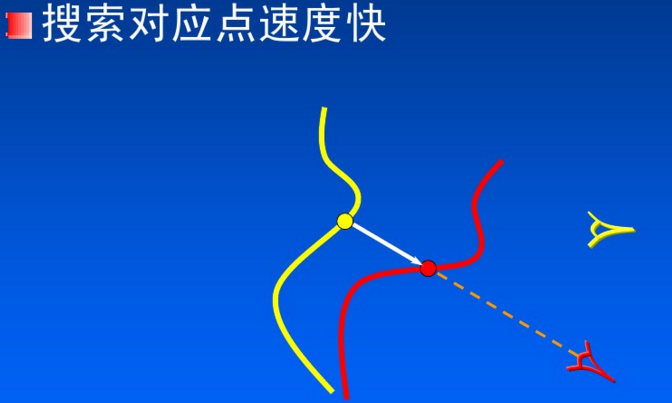