- 目錄
- 1、SVD是什么、表達式是什么及對應的數學含義;
- 2、了解方陣、行列式的含義(方陣即矩陣,行列式即矩陣的計算結果)
- 3、了解代數余子式的概念
- 4、伴隨矩陣的概念
- 5、知道方陣的逆的公式、范德蒙行列式
- 6、知道矩陣的乘法,掌握狀態轉移矩陣。
- 7、知道矩陣的秩的概念
- 8、知道系數矩陣、正交陣、正定陣
- 9、掌握特征值和特征向量
目錄
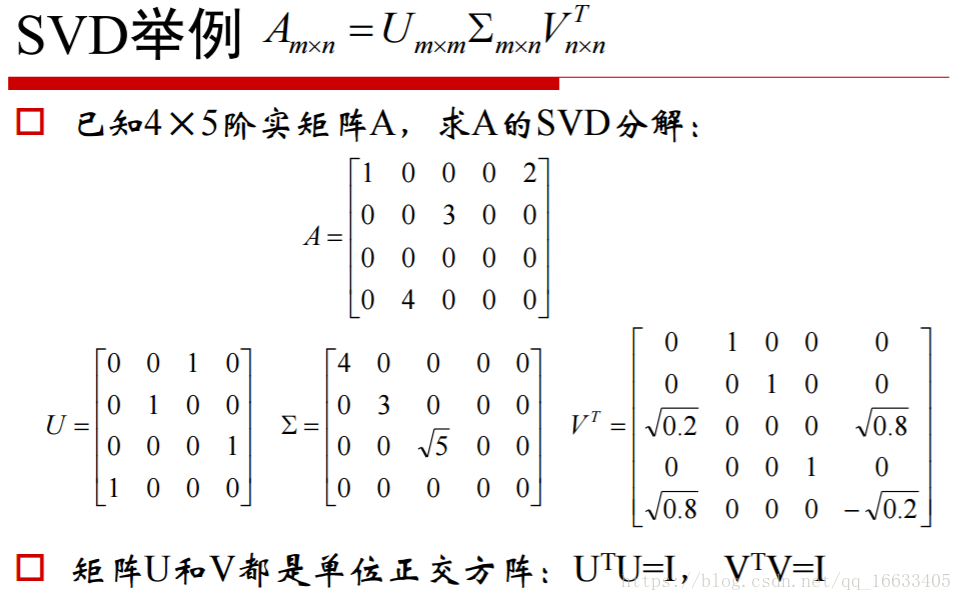
1、SVD是什么、表達式是什么及對應的數學含義;

2、了解方陣、行列式的含義(方陣即矩陣,行列式即矩陣的計算結果)
3、了解代數余子式的概念
將一個元素所在的列和行劃去后,剩余的方陣稱為該元素的余子式。代數余子式也就是余子式的代數表示形式。
4、伴隨矩陣的概念
每個元素的代數余子式所構成的方陣稱為A的伴隨矩陣
5、知道方陣的逆的公式、范德蒙行列式

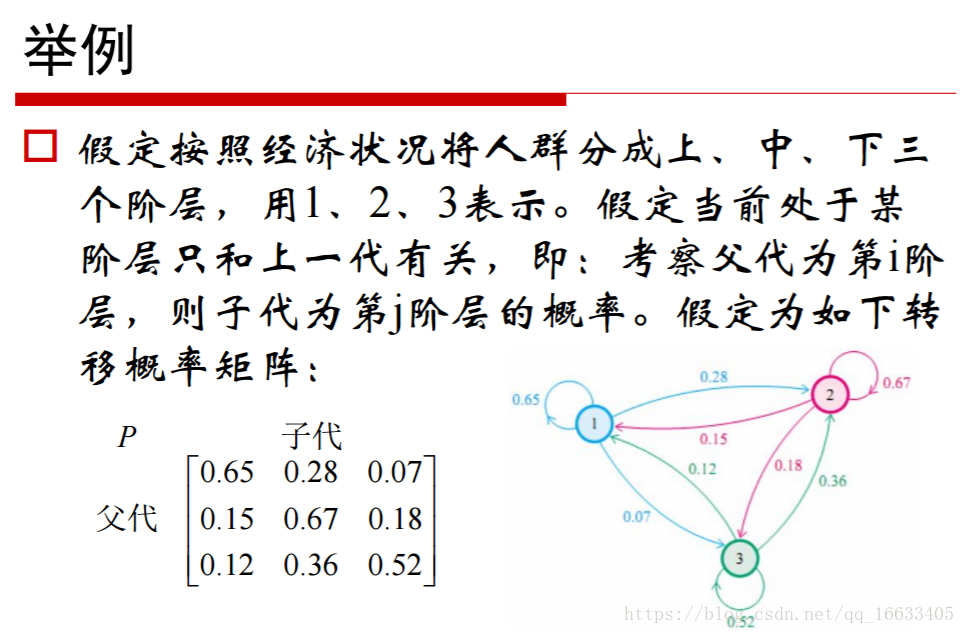
6、知道矩陣的乘法,掌握狀態轉移矩陣。
矩陣的乘法實際上對應的是一個維度的空間到另一維度空間的映射。
狀態轉移矩陣(又稱轉移概率矩陣):矩陣各元素都是非負的,并且各行元素之和等于1,各元素用概率表示,在一定條件下是互相轉移的,故稱為轉移概率矩陣。

7、知道矩陣的秩的概念
首先知道k階子式的概念即在矩陣A中任取K行K列,不改變這些元素的順序,則這個K階方陣稱為矩陣A的K階子式。
其次,若在矩陣A中有一個不等于0的r階子式D,且所有的r+1階子式全等于0,那么r稱為矩陣A的秩。


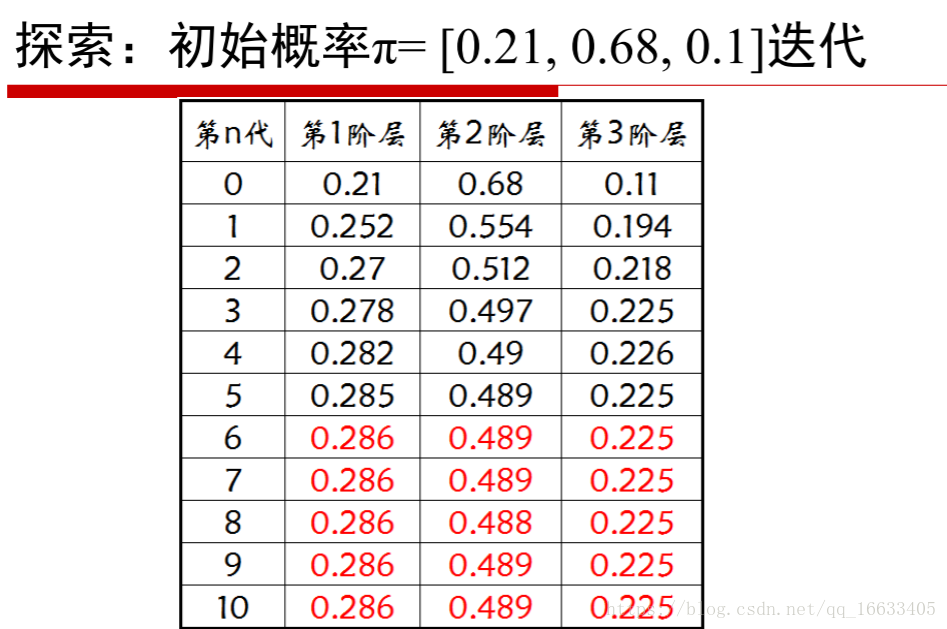
即初始概率乘以概率轉移矩陣P的N次方,不斷的迭代即得到最終的穩定值。
8、知道系數矩陣、正交陣、正定陣


知道正定陣即代表正數在N維空間中推廣
9、掌握特征值和特征向量
特征值可以理解為系數矩陣的絕對值。X稱為A對應的特征向量。了解特征值的求法及性質。








教程六:創建并發送帶有附件的郵件)







 格式)




{}))
總結)

.scroll(function())
---- JDBC)