1、知道提升、梯度提升是什么意思

1.1、提升

每一步產生一個弱預測模型，并加權累加到總模型中。

1.2、梯度提升

如果每一步的預測模型生成都是依據損失函數的梯度方向，則稱之為梯度提升。

1.3、了解提升算法的過程

處理的過程：拿原始數據x,y生成一棵樹（得到一個相應的函數T（xi）），得到對應的根據點預測值。之后計算原始數據和預測值的殘差（殘差盡可能接近于0）作為損失函數（殘差是觀測值與預測值之間的差），如果不等于0則將殘差作為xi的“y”再生成一棵樹，再得到對應的預測值Yi，再次計算”y”和預測值Y^的殘差值（也就是預測值和殘差值的殘差值），看損失函數的值是否為0，若不為0則重復以上步驟…直到損失函數為0.（提升算法的損失函數是預測值和真實值的殘差）

2、殘差與殘差平方和（residual sum of squares）

殘差：是指觀測值與預測值（擬合值）之間的差，即是實際觀察值與回歸估計值的差，把每個殘差的平方后加起來 稱為殘差平方和，它表示隨機誤差的效應。
每一點的y值的估計值和實際值的差的平方之和稱為殘差平方和,而y的實際值和平均值的差的平方之和稱為總平方和。
誤差:即觀測值與真實值的偏離;
殘差:觀測值與擬合值的偏離.
誤差與殘差，這兩個概念在某程度上具有很大的相似性，都是衡量不確定性的指標，可是兩者又存在區別。
誤差與測量有關，誤差大小可以衡量測量的準確性，誤差越大則表示測量越不準確。
誤差分為兩類：系統誤差與隨機誤差。其中，系統誤差與測量方案有關，通過改進測量方案可以避免系統誤差。隨機誤差與觀測者，測量工具，被觀測物體的性質有關，只能盡量減小，卻不能避免。
殘差――與預測有關，殘差大小可以衡量預測的準確性。殘差越大表示預測越不準確。殘差與數據本身的分布特性，回歸方程的選擇有關。
誤差大,由異常值引起.表明數據可能有嚴重的測量錯誤;或者所選模型不合適,;
殘差大,表明樣本不具代表性,也有可能由特征值引起.
總之要看一個模型是否合適,看誤差;要看所取樣本是否合適,看殘差;

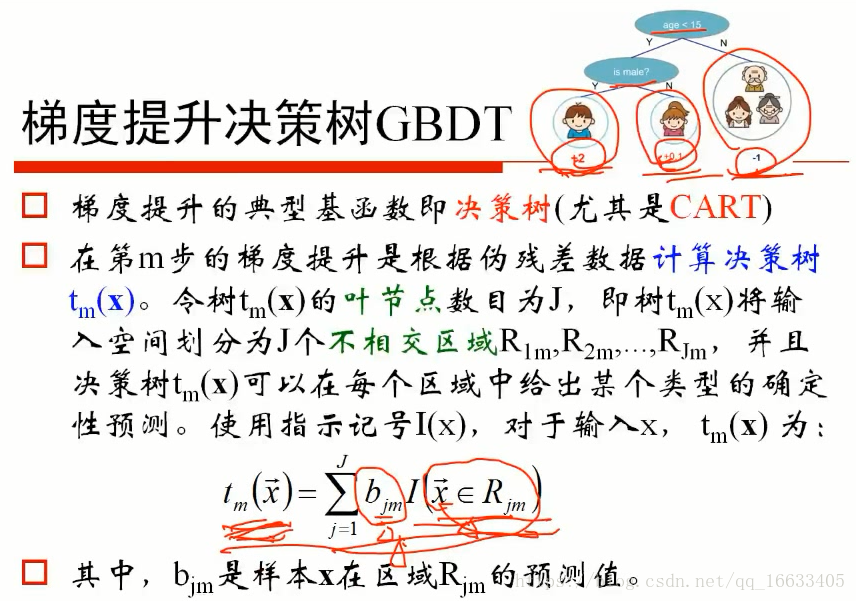
3、了解GBDT算法

了解GBDT計算決策樹的公式Tm(x）也就代表決策樹函數（即輸入x得到預測值），其中Bjm代表的是樣本X在區域Rjm的預測值（Rjm決策樹的幾個葉子節點），I代表的是x是否該區域（是的話為1，不是的話為0）

4、了解XGBoost算法

XGBoost算法只是將目標函數改為了二階導信息
XGBoost生成樹的過程：枚舉可行的分割點（下圖五個數據有4種分割），然后依次計算對應的Gain()（根節點的損失減去兩個葉節點的損失得到一個增益值），選取增益最大的劃分。
依次進行得到整棵樹。由此也能得到對應的權值w（參考w的計算公式）。

5、了解Adaboost算法

5.1、Adaboost算法的原理

通過初始化權值得到對應的誤差率，進而得到加權系數，之后利用公式不斷的迭代初始權值直到目標函數達到最優。
權值是需要初始化即D

em（誤差率）可以計算出來（就相當于判斷預測值和實際值是否相等），知道em后就能計算出對應的Gm(x)對應的系數αm了。

由下圖中的公式計算Wm+1的值(α、樣本的實際值和預測值以及對應樣本的權值都為已知條件)，去更新數據集D1中對應的權值得到D2，之后再計算D2對應的誤差率e2和對應的系數α2…依次類推直到最后。（exp，高等數學里以自然常數e為底的指數函數）

由算到的m個α系數和對應的預測值相乘相加得到最終的總分類器
f（x）：基本分類器的線性組合。

αm的值是>0的（1-em>em即誤差率小于0.5）

迭代過程中預測結果對權值的影響：即實際操作中當預測結果正確時，第二次迭代時對應的權值會減小，反之則會增加。
Wmi公式中的值都能得到。

5.2、例子

選取一個閾值使基本分類器G1（x）的誤差率最小。

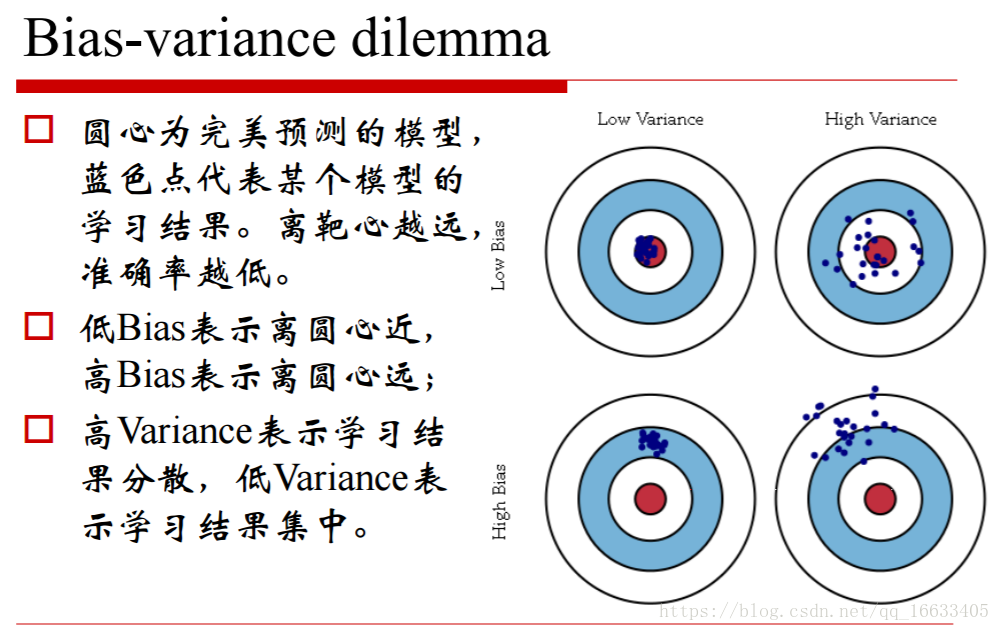
6、偏差和方差

知道偏差和方差：把偏差認為是單個模型的擬合能力，而方差則描述的是同一個學習算法在不同數據集的不穩定性
偏差與方差：
偏差描述的是算法的預測的平均值和真實值的關系（可以想象成算法的擬合能力如何），而方差描述的是同一個算法在不同數據集上的預測值和所有數據集上的平均預測值之間的關系（可以想象成算法的穩定性如何）。