序言： 本文將以維度為主線， 帶量大家進入非線性動力學的世界。 文章數學部分不需要全部理解， 理解思維方法為主

非線性動力學，是物理學的思維進入傳統方法所不能解決的問題的一座豐碑。它可以幫助我們理解不同復雜度和時間空間尺度的系統，小到生物細胞的代謝反應， 大到社會運行的規律。 并且在當下對神經網絡的理解中起到越來越重要的作用。??

從牛頓開始， 所有動力學的核心使命是預測系統的變化，非線性動力學在這點上也是一樣的。一個經典的非線性動力學系統具有標準的表述形式：

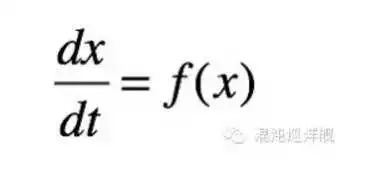
預測一個系統的未來，你需要知道它在微小時間尺度里的性質并列出動力學方程(上圖)。

此處X是一個向量(vector)，它所具有的分量個數即系統的維度。維度是動力學系統的最基本屬性 。它決定系統的復雜性，及其可能具有的基本性質。 還有，我們有多大把握預測系統的未來。

最簡單的系統是一維系統，也就是x只包含一個變量的情況。 預測一個一維的非線性系統，往往只需抓住一個關鍵性信息-定點。

I 一維系統與定點(Fix Point) “反饋導致平衡”

一維的系統， 往往抓住反饋即可。 反饋導致平衡，?非線性動力學用定點fix point來描述這種現象。 為什么fix point 普遍存在？ 因為負反饋的普遍存在。當一個事物像一個方向走的太遠，就往往有一種反方向的作用力把它拉回，有點像我們所說的物極必反或陰陽相抵。

一個典型的一維系統模型就是人口模型。這其實符合一個叫做Logistic Model的經典一維動力學模型, 它也因它那美妙絕倫的S曲線而聞名。這個模型說的是，在沒有環境壓力的時候(人人吃飽飯)人口的增長率是恒定的，所以如果第一年是2，那么第N+1年即使2的N次方(幾何增長)，但是一旦人口接近環境的閾值，就會有人開始餓死，而這個餓死的比例隨著人口的增長而增大(負反饋)。這樣，當餓死的人等于出生的人，兩個此消彼長的要素就在某個點上平衡了。 所謂定點。

反映在數學上，就是這樣一個微分方程 ：

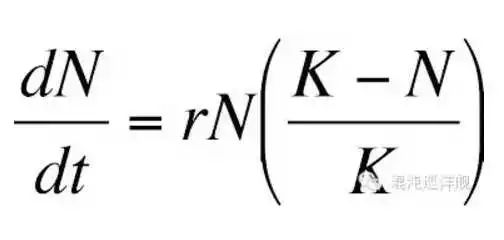
人口的變化取決于兩個相乘的因子，一個描述增長 (rN)，一個描述饑餓(1-K/N)。 定點，就是使微分(人口變化率)為0的點，當人口數恰好處在這個點上，就會不增不減。

這個定點具有一個更深刻的性質，無論你的人口一開始是多少，只要K給定，系統都會趨于一個相同的值。這個值由環境本身的容量所確定。

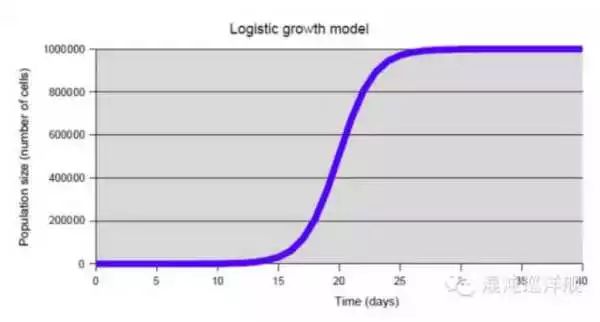
這個微分方程的解是一條優美的S型曲線(Sigmoid Function)，它的身影在自然界中比比皆是，反映了自然生長的一般規律。

理解動力學系統最重要的工具是相圖：所謂相圖， 是以系統的變量為坐標軸， 概括了系統從任何初始狀態(x0)開始演化， 它的未來發展軌跡。每個箭頭對應該點的dx(變化量，衡量系統在該點運動趨勢)。相圖告訴我們系統在任何情況下的發展走勢， 是對世界的高度概括性表達。??

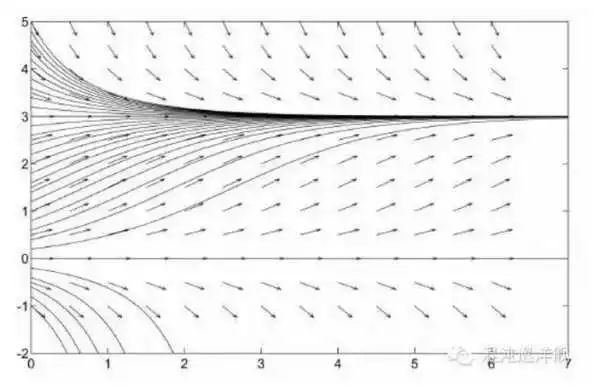
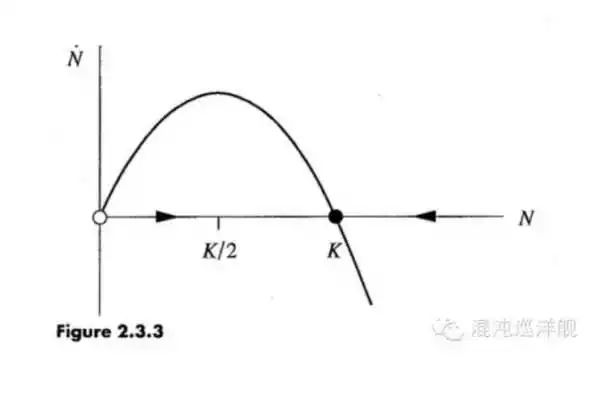
注： 上圖為系統N隨時間的變化， 不同的曲線代表從不同初始位置出發的結果。箭頭帶表N變化的趨勢。 下圖是N的導數和N的關系圖，可以看到使得N導為0的N值即系統的定點，這里是0和K。

定點的穩定性：

動力學里最重要的概念-定點(fix point)，但是定點本身卻只具有系統很少的信息，更關鍵的性質來自于對定點周圍區域的分析。 或者說定點的穩定性。

那在一些情況里，定點好想是系統變化的宿命。起點還是什么都不重要，你不需要擔心輸在起跑線上，只要你起跑了，就會到一個地方-定點。 而在另一些情況里，定點雖然存在，但是你只有在極特殊的條件下才能達到，類似于屌絲逆襲，屌絲的逆襲是有的，但是要有極好的運氣+相當高的智慧才行。即使你達到了這樣的定點，稍有風吹草動也會失去它。

我們用一個叫做穩定性的概念來描述這一特性。穩定性是描述當系統處在定點周邊的狀態，它是比較容易進到定點還是離開它。

一個典型的例子是單擺, 單擺的微分方程有兩個取零的點，但是你通常看到擺處在最低點卻極少有機會看到一個處在頂點的單擺。原因很簡單，單擺的低谷是穩定定點而高點是不穩定的。 除非你一開始就靜止在最高點而且排除任何外力，否則最輕微的偏離就可以導致單擺回到穩定的最低點。

在物理的角度很容易理解一個定點是穩定的還是不穩定的，只需要稍微的離開定點，看一下系統的運動情況，看看系統在定點的相鄰區域里的運動趨勢怎么隨位置變化。而這翻譯成動力學語言就是在定點周圍進行泰勒展開，并取一階線性近似(在一維得到一個線性的斜率，高維就是雅可比矩陣的特征值)。如果在定點周圍的運動趨勢指向定點(線性的斜率為負，雅可比矩陣特征值為負)，則定點在局域內穩定，反之則局域不穩定。

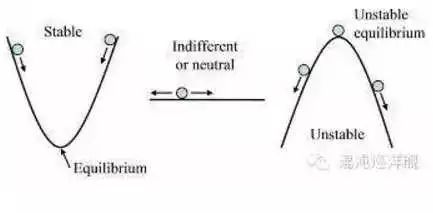
注：定點的穩定性，取決于泰勒展開的不為零的第一項的正負。左圖為穩定平衡，右圖為不穩定平衡，雖然均為定點，但周邊性質迥異。

穩定性，換一個詞叫吸引力。一個穩定性定點，就像一個區域的主人，它能把進入其轄區內的所有人都吸收到它的點上。它所管轄的區域，稱為-Basin of Attraction。它是強韌性的代表，無論你怎么干擾它，迫害它，結局都將歸于它。找到Basin of attraction 是利用定點預測系統的必備條件，給定一個系統，如果它的初始位置處在basin of attraction，那么它必歸于定點。

不穩定性呢，就是脆弱性的代表了。任何環境的風吹草動都能結束她表面的美麗。如同得了艾滋病的人，今天看著好好的，隨便一個病毒就可以摧毀他。

最強的定點具有全局穩定性，即無論任何初始條件，系統都將趨于這樣的定點，這樣的系統就是高度可預測系統。

很多系統往往具備一個穩定點和一個不穩定點成對出現。比如剛才的人口模型，人口為0就是一個不穩定平衡點。當人口為0的時候，它可以永遠為0，但只要系統的人口增長了1，它就會趨于定點K，掌控系統除0之外所有區域的穩定點。

算命先生往往就是掌握動力學定點理論的人，它們往往根據一些片段的細節，做出一些“大膽”的預測，比如看到一個20歲左右打扮漂亮的女士，就會說你會有一個有錢的老公，漂亮的房子一類，看到滿手老繭的老媽子就會說你一定一切為丈夫和孩子操心了一輩子一類。 它們往往知道系統有一個穩定點和一個不穩定點，美麗的大姑娘找到幸福美滿的婚姻呢是穩定點，跟了一個窮二代是不穩定。滄桑的老嫗為家庭奔波一生是穩定點，風流一生是不穩定點，所以有50%以上概率命中就不足為奇了。

判斷簡單系統，抓住定點就是抓住了命門。

II. 二維動力學系統 - 眾妙之門

請先看下面幾個問題，

為什么從自然到經濟現象， 振動(周期)普遍存在？

為什么物理中的變化往往是線性的，而生命和經濟社會現象里，變化經常是突變的形式？?

為什么看似隨機的神經網絡可以具有非常復雜的認知功能？

所有這些，我們都可以用非線性動力學來了解， 而這一切理解的基礎是二維的動力學系統。 二維可以描述比一維豐富多的現象，正如通物理學從描述兩個物體的相互作用開始描述了世界。

這里， 我們從最簡單的系統-二維的線性動力學系統開始， 定義為：

dx= ax+by

dy = cx + dy?

可以由一個a，b，c，d組成的二維矩陣(雅可比矩陣A)刻畫(dX/dt = AX)。 這個兩兩作用的系統在自然界比比皆是， 比如著名的獵手-獵物方程。

對于任何動力學系統， 我們都要先抓住它的定點， 而整個系統的性質， 由定點向外周擴散迎刃而解。 那么這個簡單的線性系統有一個顯而易見的定點就是x=0， y=0.

定點的作用就像一個巨大的吸引中心， 系統的演化無論多么復雜， 都是以某種形式圍繞它展開。 有了定點后， 系統具體的演化方法則由它的雅可比矩陣決定。 在這里雅可比矩陣也就是abcd所確定的連接矩陣A 為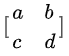這個矩陣里的各個元素，它將確定，隨著時間，系統將去向何方。 我們可以按照特征矩陣的行列式det A = ad -bc 以及跡(traceA) a +d 作為坐標軸對系統分類。為什么是這兩個東西， 你想一下， 矩陣本身由特征值決定， 在特征分解后，A代表特征值的乘積，trace是特征值的和， 這兩個量體現了特征值的性質。 矩陣的特征值是一個復數， 對應復平面上的兩個點。 這兩個點的幾何性質由剛剛說的行列式和跡決定。

數學的好處在于一次得到所有的可能性。 一切可能皆由定點展開， 這些情況按照定點穩定與否(演化是趨緊還是遠離它)， 以及趨于(或遠離)定點的方式展開。 那么二維系統圍繞定點有多少變化形式？?

我們通常用poincare diagram 來表達所有情況。 從左向右， 定點從穩定到不穩定(特征值由負到正)，從下到上， 趨于或離開定點的方式由線性變換到旋轉(特征值由實入虛， 此處以delta=traceA**2 - 4* detA為界)。方程你可以把整個解析解寫出來 X=(x，y)

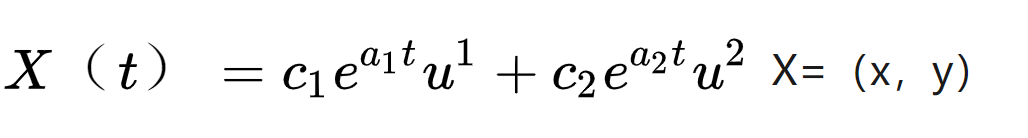
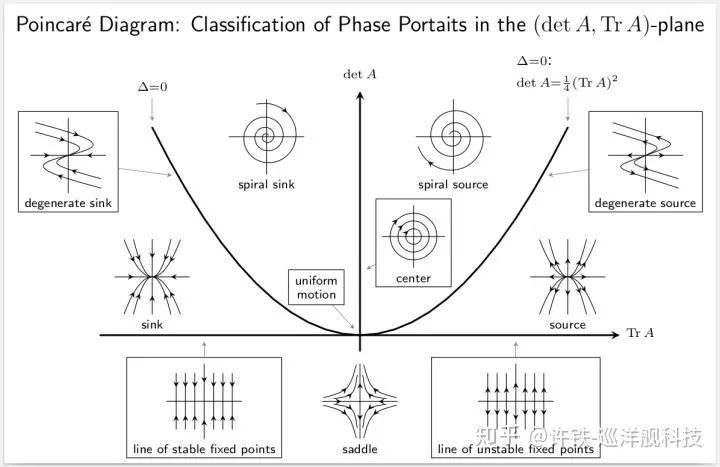
由如上的兩個坐標軸和一個拋物線，我們把平面分割成了6個區域。 你只需要記住臨界態的性質， 中間區域及其過渡。 抓住這個平面，就抓住了所有的二維線性動力系統。而這里的每個趨于，都代表系統的一個變化形式。?

y軸上半? 此處特征值為純虛數， 實部為0， 我們既不趨近也不遠離， 這也就是周期運動， 或被稱為極限環。 系統圍繞定點做圓周運動，是穩定和不穩定的過度狀態。 典型例子如二維諧振子 - 理解各種復雜的物理系統的畢達哥拉斯之劍。 加入一定非線性形式我們得到獵手-獵物方程， 狼和羊， 資本和勞動力矛盾下的振動平衡。 自然界還是人類現象中振動如此普遍， 背后正是這類動力關系的體現。

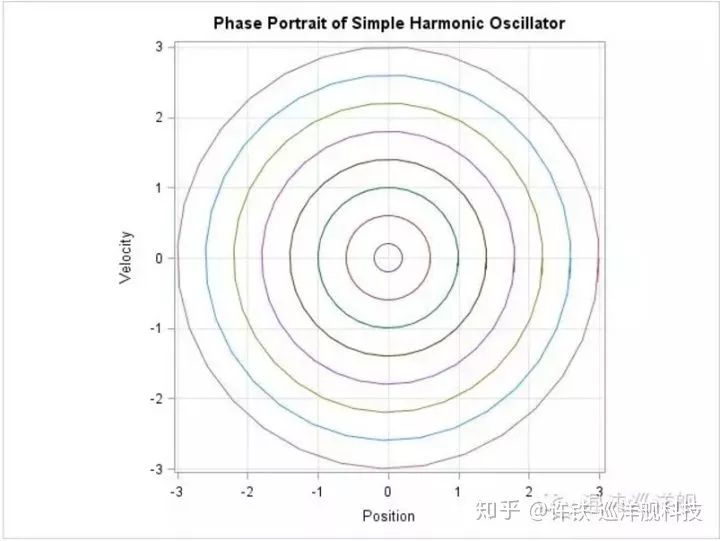
振動是伴隨二維系統最重要的現象預測， 同時它的出現往往寓意了系統的背后有兩個作為主要矛盾的變量。?

為什么振動的形式這么廣泛的存在？ 其實依然是因為定點的廣泛存在， 所謂振動，無非圍繞一個卻確定的狀態的上下波動。?就好像那希臘神話痛苦的西西弗斯，把石頭推上山，可它卻滾下去，然后他又推上山， 他想叫石頭停在山上不動，可他就是達不到。

X軸下半和det中間區域?穩定定點， 代表趨勢所致， 穩定定點可以預測事物的一般走勢(穩定不變的平衡態，任何遠離它的陰謀都將破滅)，因為在它的管轄區域里， 無論如何折騰， 都回回到它， 因此穩定定點也可以用來存儲信息。 此處同一維系統。

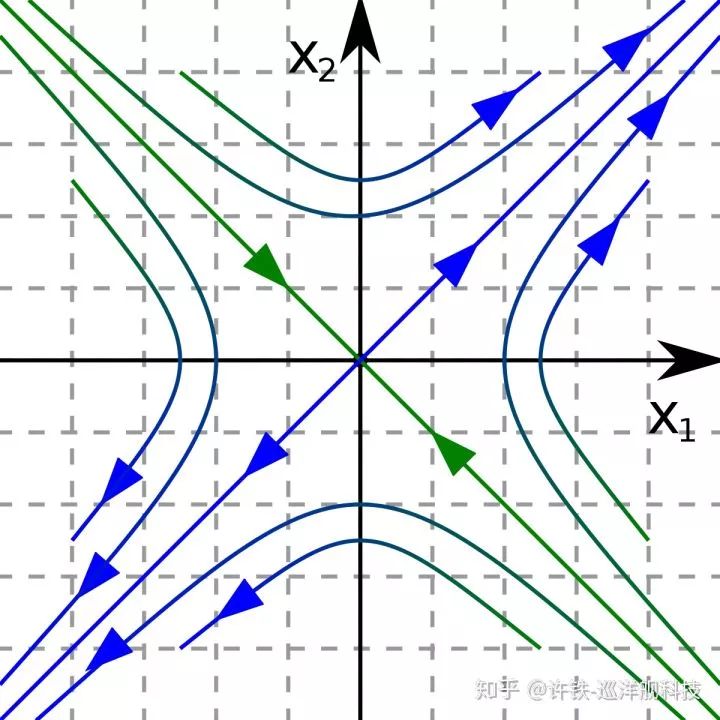
Y軸下半及整個下半平面：鞍點(Saddle)與上半的區別在于運動方式， 剛剛說的轉動變成線性， 然而依然是從穩定到不穩定的臨界，此處的效果是從一個特征向量方向你趨于定點(穩定)，而另一個方向則遠離(不穩定)。 這樣的系統可以表示神經網絡的決策或分類： 從一個方向得到的結果是A， 從另一些方向得到的結果是B，這就是天然的分類器。鞍點也用來介導一個動力系統的相變， 從一個方向你達到定點， 再在另外一個方向分離， 例如所有的熱戀到失戀的過程。?

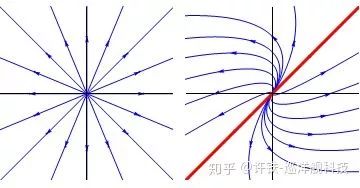
X軸： 剛剛那個圖一個更加特殊的情況是X軸上(det 為0)的那些解，這條線的數學含義是我們某個特征值為0的情況(此時矩陣的跡為0)， 啥叫特征值為0？ 它意味著只要我們在這個為0的特征值所對應的特征向量，我們就有

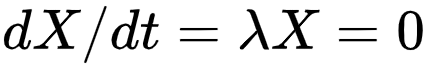
，也就是特征向量方向的所有解都是定點！ 而它導致的結果是所謂的線性吸引子， 定點不在是一點而是一條線(line attractor)。 我們會看到這個解在眾多的問題里意義重大，比如神經編碼 。這是因為線性吸引子是路徑依賴的代言人， 你從不同的起點出發， 會停留在不同的位置上， 這就好像把初刻的歷史凝固了下來，因為可以比單個穩定定點編碼更復雜的信息-甚至是某種抽象關系。

非線性的作用：?

剛剛求解的是一個二維線性系統，我們 而一旦加入非線性，就成為非線性系統， 如：

dx= f(x，y)

dy =g(x，y)

f和g包含非線性， 那么這個時候可能性就更多 ， 而事實上我們依然是利用我們在線性系統的知識來研究這樣的系統。 最典型的方法就是先找定點， 然后在定點周圍線性化。

對于非線性的二維系統， 最大的變化是定點不再只有一個， 你去求解f(x，y)=0? ?； g(x，y)=0 的連鎖方程即可。?

對于非線性的世界， 幾何與拓撲的思維有時候比代數更迅速的幫我找到系統的本性，及大趨勢。?

此處引入一個體現這一思維的經典理論。 龐加萊定理： Poincare-Bendixson Theorem：

條件：

1.2D - 你有一個二維的動力學系統

2.Continous - 系統連續可微

3. Confined - 動力學流在一個區域內封閉

4. No Fix point- 在此區域內定點不可達到

結論：

該區域內的動力學流將收斂于一條閉合軌道(等價于圓)。

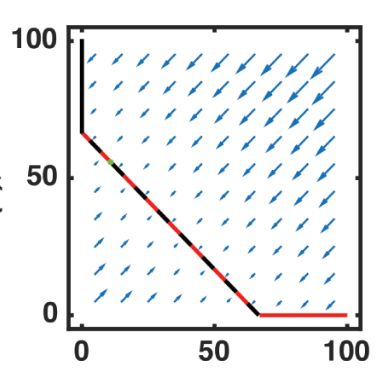
翻譯一下，相平面的閉合軌道=周期性運動=振動。 這個定理告訴我們，有限二維系統里的運動形式只有有兩種： 1. 平衡態(歸于定點) 2. 周期運動。 不存在其它情況。 有限只得是系統不會無限取值或發散。由于自然中負反饋的普遍存在這一條一般是滿足的。 這條定律解釋了振動普遍存在的根本原因，因為它是二維運動的范式。

圖為相平面上的閉合軌道，龐加萊引理告訴我們，如果整個系統是收斂的，二維動力學流非流向定點即指向閉合軌道。

狩獵者- 獵物系統：?

二維非線性系統一個最典型的例子依然是延續我們關于物種數量的故事，剛才講到一維的人口模型里人口將達到定值，而事實自然界中的物種數量卻是震蕩變化的，為什么？

解答這個問題，就需要討論兩個物種共存的情況(二維)，試問下面的問題， 在一片草原里生活著獅子和羚羊，獅子吃羚羊，羚羊吃草(假設無限)，假設一開始物種數量是均等的，那么后來兩個物種的數量變化會是怎么樣的？ 顯然，兩種物種間有相互作用， 獅子的存在依賴于羊(簡單的想法是羊肉變成了獅子)，而羊的數量因為獅子而減少，如果沒有獅子，羊的數量增長就符合之前的S曲線：

這樣一個系統可以被一個Lotka-Volterra 方程的經典二維動力學系統表述:

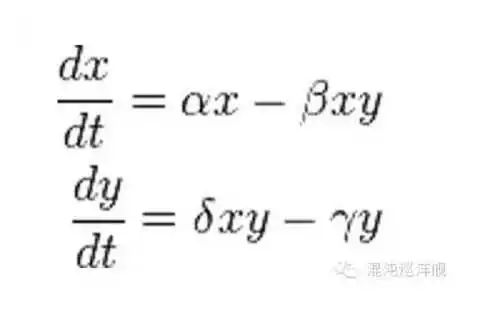
這個方程極為容易理解。系統的兩個變量一個是羊的數量(x)，一個是獅子的數量(y)。 第一項描述羊的自然生長率。 第二項描述羊被吃的數量，x和y的乘積決定兩個物種相遇的機會， 所以羊被吃的速率正比于xy。相應的，獅子可以理解為由羊肉轉化出來的，所以其增長率正比于捕獲的羊數量(方程二第一項)，方程二最后一項描述獅子的死亡率。

那么，如何預測兩種物種數量變化？首先進入相平面， 我們看到系統的流形(每一點的微分(dx，dy)構成一個向量，畫出箭頭猶如流體力學的流速線)。 然后我們分析定點，二維系統里含有兩個微分方程，如果一個微分方程為0，例如dx=0，我們得到一個代數關系 x=k*xy. 在相平面里這對應一條線-Nullcline，在這條線上，第一個變量處于平衡態。 同樣的我們可以找到變量y的Nullcline， 對應相平面的另一條線，這兩條線如果有交點，即二維系統的定點，或者說系統的平衡態。

但是至關重要的是討論定點的穩定性而非平衡態本身。

這個問題可以很容易的找到四條Nullcline和兩個定點： 一個是(0，0)，另一個第一象限中的(a,b)， (0，0)代表的兩個物種都滅絕了。 這種情況除非是羊死光了才可能出現，而假如是獅子死光了，羊就會無限增長(遠離定點)。 在相平面上，就表現為動力學流沿著y軸(對應羊死光的情況)收斂為0，而沿著x軸(對應獅子死光的情況)發散。這一現象的隱含含義是(0，0)點在x方向上是不穩定性定點，而在y方向上是穩定性定點。 這種在一定方向上收斂，而在另一些方向上發散的定點，被我們稱為Saddle Point(鞍點)，就是剛剛在線性系統介紹過的那個。?

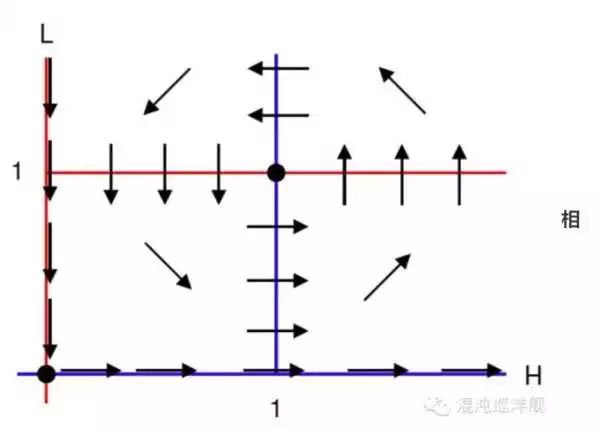
相平面的動力學流

在看看第一象限內的定點(a，b)，它描述兩個物種數量互相制約的平衡狀態， 看似這是一個合理的結局。獅子和羊的數量打到平衡，這不就是那啥生態平衡嗎？ 那你停留在初中生物課本了。在這個定點周圍找幾個點，畫畫(dx，dy)的箭頭你就知，它們都不是朝向這一點，而是圍著這點轉圈。 利用我們神一樣的龐加萊大法可知。 系統將永不能陷入這個點(除非它一開始別上帝設定好就在那個位置)。而是圍繞這個點形成閉合軌道-即振蕩。 系統的兩個物種的初始數量只要不是有一個滅絕或恰好開始就匹配平衡， 都將行成一個振動變化關系。

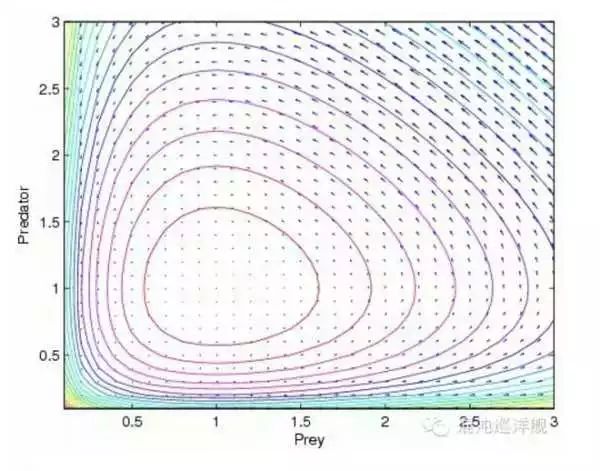
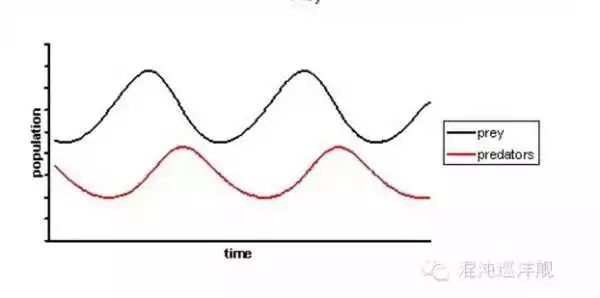
獅子和羊在固定系統里的數量成周期震蕩。上圖為相平面，下圖為兩個物種數量隨時間變化關系。

整個生態學可以用動力學語言描述。其核心議題，生態系統的穩定性正是動力學最拿手的分析內容。

Lotka-Volterra 系統在經濟學中也有重要應用。凱恩斯學派用以解釋勞動雇用率和資本的周期震蕩。這一理論把資本對應為獅子，而勞動雇用率是獵物，兩者總是不能自發的處于定點(100%雇用率)而是進入周而復始的震蕩狀態。

III 高維系統與RNN

理解了二維系統， 你可以抓住它內在本質的東西， 然后一級級向高維延申。 我們將在此處開啟一個在人工智能和腦科學都極為重要的模型-RNN，?

它的線性形式

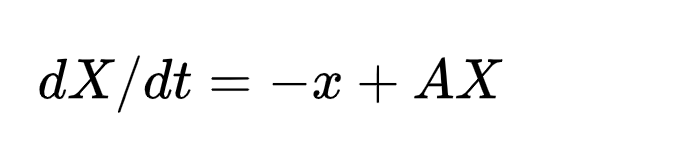
非線性形式：

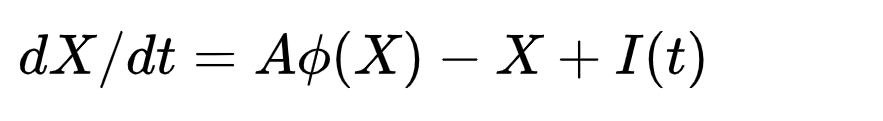
事實上RNN可以理解為一個通用的高維非線性系統， 它代表了各種自然界的復雜網絡的一般形式，從人腦神經元網絡， 到生態網絡， 到社會經濟網絡。?

RNN最重要的東西就是網絡連接A， 刻畫神經元和神經元的連接， 它的最一般形式被稱為隨機矩陣。?

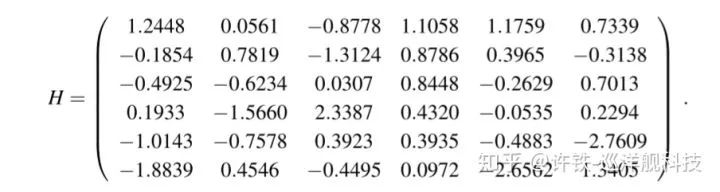
隨機矩陣刻畫一個高維動力系統， 其不同單元間的連接是隨機的。 如果我們假定高維系統依然是線性的， 那么它一般寫成：

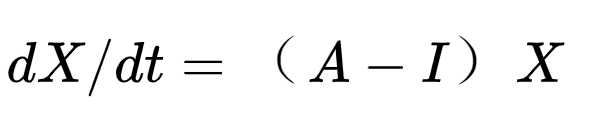
A是一個nxn的方陣， 由剛剛說的隨機數確定。

這個矩陣A如何決定系統性質呢？ 首先， 尋找定點，?這樣的解有一個是肯定的，就是 X=0

其余性質將由矩陣的特征值和特征向量決定。 我們對連接矩陣A進行特征分解， 得到一系列的特征值和特征向量， 我首先讓你猜一下如果你把它的特征值和特征向量在復平面上展開， 它們會長成什么樣呢？

你依然從二維線性系統， 一個2x2的方陣入手。 這個矩陣的特征值如果你畫在復平面上長什么樣呢？ 這一類矩陣有兩個最特別的情形， 一個對角線為0實對稱?

?，?

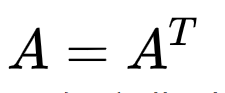
一個對角線為0的反對稱?

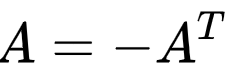
假定矩陣元素為a，對于情況一我們得到的兩個特征值是-a和a的兩個實數， 對于情況2我們有-ai和ai也就是把它們換到虛軸上(這正是剛剛說的諧振子解)。 由此你進行一個類推， 如果我的矩陣的元素不在是這兩個特殊情況而是隨機的， 我只保證這些矩陣元素每個的期望均是0， 然后你要求出特征值的分布會是什么樣的？ 剛剛的解一個是沿著實軸相對原點對稱， 一個是沿著虛軸相對原點對稱。 如果綜合起來呢？ 在實軸和虛軸組成的復平面上， 我們會得到任意方向沿著原點對稱的一組點， 從而組成最完美的一個圖形- 也就是， 一個圓！ 具體求解請見論文(Introduction to Random Matrices-Theory and Practice)。

好了， 那么維度增加呢？ 當你的矩陣元素越來越多， 這個時候我的高維矩陣的特征值個數將等于我們的矩陣維數， 當這個數字達到一定程度， 我們任意一個矩陣的特征值都將逼近剛剛說的那個所有可能二維矩陣的特征分布， 也就是一個圓，至少非常接近！?

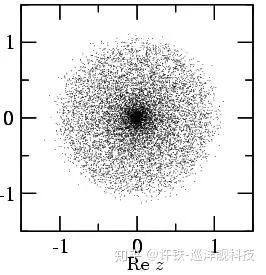
好了， 從這里我們可以立刻領悟到的是什么？ 首先， 高維系統圍繞定點的變化形式更加多變， 因為每個特征值都對應了一種模式， 而特征值的數量是無限的。 再有， 特征向量和特征值攜帶所有矩陣的信息， 那么所有的隨機矩陣的性質是類似的。這里只有一個東西是變化的， 就是圓的半徑。 這個量有什么意義呢？還回到二維情況進行對比， 在我們剛剛的情況里 ， 矩陣的trace從小于0到大于0引起整個系統從穩定定點過度到一個不穩定定點， 而此處， 這個圓的半徑， 正是起到類似的作用。

那么矩陣A-I的特征值正負將決定整個系統的穩定性， 這里的情況是如何呢？ 記得剛剛說的我的矩陣A元素都符合是一個平均值為0的高斯分布嗎？ A-I這個矩陣就是一個以-1為中心，以A的特征圓為半徑的圓形區域， 如果這個圓的半徑小于1， 那個特征值整體在負半平面， 系統會趨于穩定的解0。 而一旦半徑大于1，這種穩定性就被打破，在高維的系統里， 當你無法回到定點(或閉合軌跡)， 那么登場的正是我們眾所周知的混沌， 高維系統的演化進行永不停止的無序運動。 那么1呢？ 我們說， 這就是混沌和穩定的邊緣， 記得在二維的系統里， 這個地方會催生非常多的有趣現象， 比如二維諧振子， 比如線性吸引子， 而這些在高維系統里依然正確， 我們會得到各種各樣的復雜多解型， 比如-振動解。 而這正是和網絡有關的眾多有趣現象， 甚至生命本身， 產生的地點。

注：所謂混沌， 事實上是一大類不同動力學現象的統稱， 它們的共同特點是從某個無限接近的初始點出發， 未來的軌跡是發散的，也就是在某個初始位置上改變一點，未來完全改變， 這是一種極致的路徑依賴的體現。 混沌的最簡單形式是三維非線性方程的洛倫茲吸引子， 在此情況下事實上我們的軌跡圍繞這兩個定點做某種“周期”運動， 只是這個周期無限復雜， 因此混沌并非等于失控， 而可以是非常復雜的信息載體。 而混沌也可以普遍的存在于高維的線性系統里。 混沌可以簡單， 也可以復雜， 取決于背后的動力系統。

我們說， 這個特征譜一來決定穩定性， 而來決定趨于定點的方式。 實數代表線性的推進， 虛數代表振動，具體是哪種方式推進， 則決定于你是否在某個特征值對應的特征向量方向上。 我們知道， 我們是一個高維的線性系統，在這個高維王國里， 光坐標軸就可以建立維數N個， 那么對應的就是N個特征向量方向。 由此決定了我們以不同的初始狀態趨近定點， 可能的結果會非常復雜多變，運動模式趨于無限。

基于這種理解我們可以做什么呢？

1， 預測高維網絡的一些基本性質： 雖然我們比較難完全預測高維系統的未來， 但是我們預測其穩定性， 我們看到， 當改變一個網絡的一個基本屬性， 比如連接強度， 就會讓網絡從穩定到不穩定，從穩定平衡趨于混沌， 那么對于生態系統和社會這意味著什么呢？ 有人說當系統的元素增加連接增強會使得系統更脆弱 ，更容易失衡， 但這僅是理解之一。 一個趨于穩定平衡的系統也通常沒有什么功能。 而混沌本身， 確可以是秩序的載體。

2， 在混沌和穩定邊緣的高維隨機動力系統具有某種全能可塑性， 如果加上一定的非線性， 則可以包含極為豐富的動力學模式， 穩定定點，周期解， 不穩定定點， 混沌， 各類復雜的吸引子， 都可以在這個區域周圍出現。這個區域動力學形式已經開始豐富， 又不像完全混沌那樣難以控制， 因此是各類學習的最佳區域。

3，作為機器學習工具 預測其它混沌系統！我們說大型的隨機網絡本身就具備一定的學習能力， 而且在很多學習任務里可以匹配其它特定設計的機器學習模型。 這里一個比較著名的例子就是蓄水池網絡。剛剛開始說的預測火焰的例子正是來自這里。

蓄水池網絡基于如下事實， 真實的復雜系統就是我們剛剛將的各種簡單系統的組成， 當你的高維混沌系統RNN包含的模式足夠多樣，它就可以像多項式擬合一樣， 通過自身的復雜模式組合逼近真實系統。

蓄水池網絡的根基，正是2提到的混沌和穩定的邊緣， 再加上非線性的激活函數, 以及外界環境的輸入I。這個微小的非線性將把系統的復雜性再推一個高度， 事實上， 一個非線性的二維系統就可以表達多于一個的定點， 而非線性的三維系統就已經可以產生混沌。 一個非線性的高維混沌系統， 其數學復雜度已經接近解析的極限。

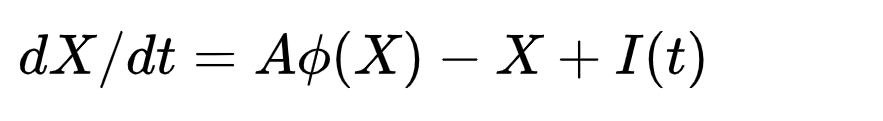
-這也就是循環神經網絡RNN。

制作一個蓄水池網絡最重要的就是控制剛剛說的特征值的譜半徑， 我們要讓它處于穩定到混沌的臨界狀態，也就似乎那個譜半徑接近1的狀態。 在這個時候， 系統的動力學屬性最為復雜，最為豐富。

蓄水池網絡具有的一種能力是， 如果你給它一個復雜的時間序列輸入(I)， 比如股市的變化， 它可以自動的抽取出這種變化背后的獨立性因子，并在一定程度模擬出真實過程的動力關系(因為其自身存在足夠豐富的動力關系， 以至于非常容易和真實的系統進行匹配)。 聽著有點像PCA，但是PCA是線性的不包含時間， 而這里是一個非線性時間依賴的系統， 復雜性不可同日而語。

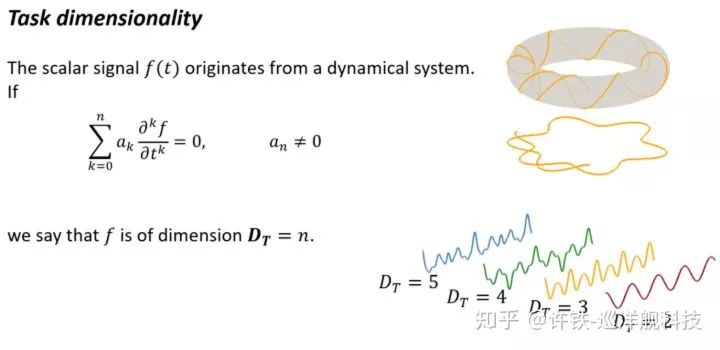
比如上面這個圖， 我們的輸入是真實世界一個很復雜的波動曲線(周期解和混沌間的過度)， 事實上多么復雜的波動背后催生它的因素不一定很復雜， 比如洛倫茨吸引子背后就僅僅是一個三維系統。

當這個波動輸入到蓄水池網絡里以后，蓄水池網絡可以找尋到這種復雜背后的根基，并對這個信號的發展走勢進行預測。

蓄水池運算的好處是不需要改變內在連接矩陣A， 我們唯一需要求解的是一個讀出, 也就是

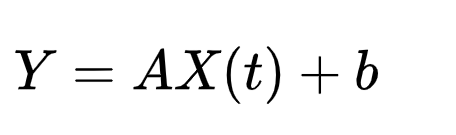
就可以對時間序列進行預測, 比如文中開頭提到的預測火焰形狀的網絡， 如下圖， 這個過程包含兩個階段，一個是訓練，一個是預測， 在訓練階段， RNN的作用事實上相當于一個auto-encoder-自編碼器， 它得到一個火焰變化的輸入， 通過網絡重現這個輸入。 而在預測階段，我們不再有火焰變化的數據，我們直接把RNN輸出的結果輸入回網絡，假設這個網絡已經學好了， 那么這個輸出就是正確的預測(下圖為實際信號(上)于預測信號的比對(下))。 這種預測能力的背后， 正是在訓練階段，RNN高維網絡里的某些成分， 抓住了真實系統變化背后的那些核心動因(自編碼器的本質即壓縮尋找主成分)。

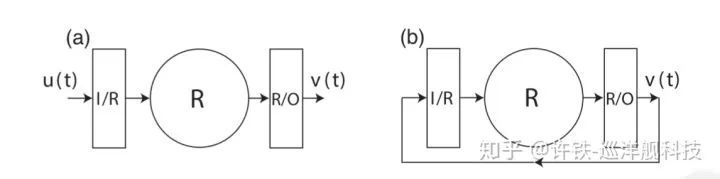
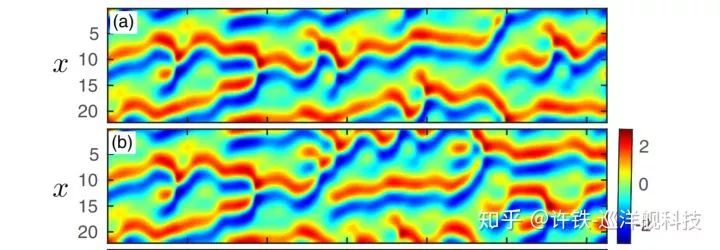
Model-Free Prediction of Large Spatiotemporally Chaotic Systems from Data: A Reservoir Computing Approach

更深刻的學習(對A進行改變)： 我們還可以做什么呢？ 在剛剛講到的各類復雜的動力學形式里， 我們看到，無論是穩定定點， 極限環，鞍點，還是線性吸引子事實上都是對世界普遍存在的信息流動形式的通用表達。 我們可以用它表達信息的提取和加工， 甚至某種程度的邏輯推理(決策)，那么只要我們能夠掌握一種學習形式有效的改變這個隨機網絡的連接，我們就有可能得到我們所需要的任何一種信息加工過程， 用幾何語言說就是，在隨機網絡的周圍， 存在著從毫無意義的運動到通用智能的幾乎所有可能性， 打開這些可能的過程如同對隨機網絡進行一個微擾， 而這個微擾通常代表了某種網絡和外在環境的耦合過程(學習)， 當網絡的動力學在低維映射里包含了真實世界的動力學本身， 通常學習就成功了。

無論當下紅極一時的鏖戰星際爭霸的網絡，還是從腦電波中解碼語言的網絡， 無非是一種特殊的RNN(LSTM)加上一定的這種學習的結果。

高維的非線性系統，可以用來描述真實世界的各種復雜網絡， 從生物基因網絡到神經網絡，到生態網絡或經濟關系網絡， 而這些網絡的驚人之處在于內在的隨機性和作為整體的強大功能。 隨機連接的市場可以極為有效的調控生產資源， 生態網絡導致微妙的生態平衡。 腦網絡產生偉大的智能， 而不同的腦網絡， 一點點連接差距確可以導致屬性的天壤之別，如人和猩猩基因差異沒有大的情況下智力確是天壤之別， 以及類似人組成的社會受到地理條件影響的微小差異后引起的社會演化巨大差異。?

這些都是看似混沌的高維系統研究可以告訴我們的，同時， 這種復雜的網絡本身也可以幫助我們來研究其它和它類似的系統， 這正是當下深度學習背后的根本， 也就是以混沌克服混沌， 對復雜對抗復雜的極好例子。??

從低維到高維， 越來越精彩。?

參考文獻：

1 Sompolinsky H, Crisanti A, Sommers H J. Chaos in random neural networks[J]. Physical review letters, 1988, 61(3): 259

2 Pathak J, Hunt B, Girvan M, et al. Model-free prediction of large spatiotemporally chaotic systems from data: A reservoir computing approach[J]. Physical review letters, 2018, 120(2): 024102.

3 Maass W, Natschl?ger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations[J]. Neural computation, 2002, 14(11): 2531-2560.

4 Schrauwen B, Verstraeten D, Van Campenhout J. An overview of reservoir computing: theory, applications and implementations[C]//Proceedings of the 15th european symposium on artificial neural networks. p. 471-482 2007. 2007: 471-482.