指數哥倫布編碼
規定語法元素的編解碼模式的描述符如下:
比特串:
b(8):任意形式的8比特字節(就是為了說明語法元素是為8個比特,沒有語法上的含義)
f(n):n位固定模式比特串(其值固定,如forbidden_zero_bit的值恒為0)
i(n):使用n比特的有符號整數(語法中沒有采用此格式)
u(n):n位無符號整數
指數哥倫布編碼:
ue(v):無符號整數指數哥倫布碼編碼的語法元素
se(v):有符號整數指數哥倫布編碼的語法元素,左位在先
te(v):舍位指數哥倫布碼編碼語法元素,左位在先
以及ce(v):CAVLC和ae(v):CABAC。
指數哥倫布編碼過程:
在表9-1中,比特串格式為“前綴1后綴”。1)1后綴=codeNum+1,如codeNum = 3,則1后綴=4,即為100,后綴為00;2)前綴與后綴的比特數相同,且前綴的各位比特為0,如codeNum=3,則最終編碼所得的比特串為:00100.
對于ue(v),按上述規則進行編碼;
對于se(v),則按照表9-3轉換成codeNum,然后按上述規則進行編碼;
在表9-3中,1)語法元素值為負數,則乘2取反,轉換成codeNum,2)語法元素為正數,則乘2減1,轉換成codeNum;
對于te(v),只有7.3.5.1節“宏塊預測語法”和7.3.5.2節“子宏塊預測語法”中的ref_idx_l0[mbPartIdx]和ref_idx_l1[mbPartIdx]用此模式編碼,
如果語法元素值為0,則編碼為1,如果語法元素值為1,則編碼為0,如果為其他大于1的值,則按ue(v)進行編碼。
---------------------------------------------------
用來表示非負整數的k階指數哥倫布碼可用如下步驟生成:
?? 1. 將數字以二進制形式寫出,去掉最低的k個比特位,之后加1
?? 2. 計算留下的比特數,將此數減一,即是需要增加的前導零個數
?? 3. 將第一步中去掉的最低k個比特位補回比特串尾部
0階指數哥倫布碼如下所示:
0 => 1 => 1
1 => 10 => 010
2 => 11 => 011
3 => 100 => 00100
4 => 101 => 00101
5 => 110 => 00110
6 => 111 => 00111
7 => 1000 => 0001000
8 => 1001 => 0001001
小波變換在圖像壓縮中的應用
小波變換在圖像壓縮中的應用
?
施吉鳴
?
摘要:近十幾年來小波理論研究已成為應用數學的一個新方向。作為數學工具,小波被迅速應用到圖像和語音分析等眾多領域。本文試圖從工程和實驗角度出發,較為直觀地探討小波變換在圖像壓縮中的應用。
關鍵詞:小波 變換 重構 圖像壓縮
?
1、小波概述
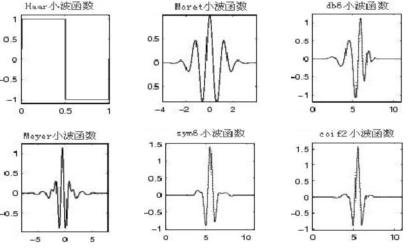
??? 小波(wavelet)是定義在有限間隔且平均值為0的函數,小波函數多以開發者名字命名,如圖1所示:
?
圖1 部分小波
?
??? 眾所周知,傅立葉分析是把一個信號分解成各種不同頻率的正弦波,因此正弦波是傅立葉變換的基函數。同樣,小波分析是把一個信號分解成由原始小波經過移位和縮放后的一系列小波,因此小波是小波變換的基函數,即小波可用作表示一些函數的基函數。
小波是近十幾年才發展并迅速應用到圖像和語音分析等眾多領域的數學工具,是繼110多年前建立傅立葉(Joseph Fourier)分析之后的一個重大突破。經過十幾年的努力,小波理論基礎已經基本建立并成為應用數學的一個新領域,引起了眾多數學家和工程技術人員的極大關注,是國際上科技學術界高度關注的前沿領域。本文試圖從工程和實驗角度出發,較為直觀地探討小波變換在圖像壓縮中的應用。
?
2、小波變換和重構
??? 小波變換的基本思想是用一組小波或基函數表示一個函數或信號,例如圖像信號。以哈爾(Haar)小波基函數為例,基本哈爾小波函數(Haar wavelet function)定義如下:
????????????????????? 1,? 當0≤x<1/2
?????????? Ψ(x) =?? -1,? 當1/2≤x<1
???????????????? 0,? 其他
設有一幅分辨率只有4個像素的一維圖像,對應像素值為:[9? 7? 3? 5]。用哈爾小波變換的過程是:計算相鄰像素對的平均值(averaging,亦可稱之為近似值approximation),得到一幅分辨率為原圖像1/2的新圖像:[8? 4]。這時圖像信息已部分丟失,為了能從2個像素組成的圖像重構出4個像素的原圖像,必須把每個像素對的第一個像素值減這個像素的平均值作為圖像的細節系數(detail coefficient)保存。因此,原圖像可用下面的兩個平均值和兩個細節系數表示:[8? 4? 1? -1]。可以把第一步變換得到的圖像進一步變換,原圖像兩級變換的過程如表1所示:
表1 哈爾小波變換過程
| 分辨率 | 平均值 | 細節系數 |
| 4 | [9? 7? 3? 5] | ? |
| 2 | [8? 4] | [1? -1] |
| 1 | [6] | [2] |
?
哈爾變換過程事實上是用求均值和差值的方法對函數或圖像進行分解,對于f(x)=[9? 7? 3? 5],我們可作最多2層的分解。
對于2維圖像,同樣可以用依次對行列進行小波變換得到2維圖像的分解。這時經過一次小波變換得到是2維圖像的近似值(CA)以及水平(CH)、垂直(CV)和對角(CD)細節分量值。顯然,從2維圖像的CA、CH、CV和CD值可以重構出原來的2維圖像。
?
3、圖像壓縮
事實上,去掉某些經過小波變換得到的細節分量值對重構圖像的質量影響不大。具體的做法是設置一個閾值δ,例如把≤δ的經小波變換得到的水平(CH)、垂直(CV)和對角(CD)細節分量值細節分量值置為0,
?

圖2 小波圖像變換過程
這樣就實現了圖像壓縮。
為了驗證圖像壓縮的效果,筆者使用數學軟件工具MATLAB 6.1設計了3級非標準小波變換和重構圖像程序function [ ] = report(picname),同時以分辨率256×256的真彩色照片為測試圖像,通過執行程序完成了閾值δ分別為0,5,10和20的情況下利用Haar小波進行變換變換和重構過程。
??? 以使用Haar小波,閾值等于10,真彩色圖像G分量為例,小波圖像變換過程如圖2所示。
?
4、實驗結論
??? 用report('jimm')對jimm_org.png真彩圖像文件計算閾值分別為0,5,10和20的情況下進行3級非標準haar小波變換和重構后,系數為“0"的數目和以PNG格式存儲的重構圖像文件大小,實驗結果得到圖像測試表如表2所示:
表2 圖像測試表
| 圖像名稱 | 閾值 | 系數為“0"的數目 | PNG文件大小 |
| 原始圖像jimm_org.png | — | — | 103KB |
| 重構圖像 jimm_haar_00.png | δ=0 | 19527 | 103KB |
| 重構圖像jimm_haar_05.png | δ≤5 | 123261 | 84KB |
| 重構圖像jimm_haar_10.png | δ≤10 | 155003 | 61KB |
| 重構圖像jimm_haar_20.png | δ≤20 | 175655 | 38KB |
?
圖3表示了在不同閾值下的重構圖像:
?

圖3 不同閾值下的重構圖像
?
從圖像測試表和觀察不同閾值下的重構圖像可得出以下結論:
u??????? 可利用小波變換與重構對圖像文件進行壓縮。
u??????? 通常在給定小波基函數條件下,閥值越大,系數為0的數目就越多,重構圖像文件壓縮率也越高,重構的圖像失真程度隨之增加。
u??????? 閥值>0時,利用小波變換與重構進行圖像壓縮是一種有損壓縮方法,可以根據實際需要在圖像失真度允許的范圍內選擇適當的閥值來確定壓縮率。
?
參考文獻
???? [1] 林福宗,《小波與小波變換》,清華大學計算機科學與技術系智能技術與系統國家重點實驗室,2001-9-25.
??? [2] The MathWorks, Inc., Wavelet Toolbox. Version 2.1 (R12.1), MATLAB 6.1 06-Apr-2001.






函數、C++)
,read(),waitKey()的使用)





)





