1. 問題描述
寫一個函數,輸入n,求斐波那契(Fibonacci)數列的第 n 項。斐波那契數列的定義如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契數列由 0 和 1 開始,之后的斐波那契數就是由之前的兩數相加而得出。
答案需要取模 1e9+7(1000000007),如計算初始結果為:1000000008,請返回 1。
示例 1:
輸入:n = 2
輸出:1
示例 2:
輸入:n = 5
輸出:5
2. 解題思路
遞歸一:
public int fib(int n) {if (n < 2)return n;return fib(n - 1) + fib(n - 2);
}
遞歸二:
當n很大的時候可能會出現數字溢出,所以我們需要用結果對1000000007求余,但實際上可能還沒有執行到最后一步就已經溢出了,所以我們需要對每一步的計算都要對1000000007求余,代碼如下(注意:下面代碼不通過,會超時)
int constant = 1000000007;public int fib(int n) {if (n < 2)return n;int first = fib(n - 1) % constant;int second = fib(n - 2) % constant;return (first + second) % constant;
}
斐波那契數列遞歸的時候會造成大量的重復計算,比如就計算fib(6)為例來看下
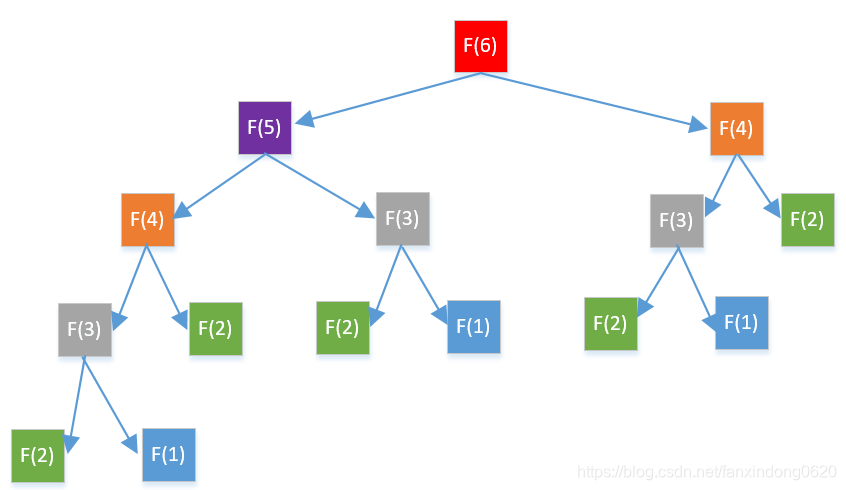
我們看到上面相同顏色的都是重復計算,當n越大,重復的越多,所以我們可以使用一個map把計算過的值存起來,每次計算的時候先看map中有沒有,如果有就表示計算過,直接從map中取,如果沒有就先計算,計算完之后再把結果存到map中。
遞歸三:
class Solution {int constant = 1000000007;public int fib(int n) {return fib(n,new HashMap());}public int fib(int n, Map<Integer,Integer> map){if (n<2){return n;}if (map.containsKey(n)){return map.get(n);}else{int first = fib(n-1,map)%constant;map.put(n-1,first);int second = fib(n-2,map)%constant;map.put(n-2,second);int result = (first+second)%constant;map.put(n,result);return result;}}
}


)




)











