目的
用勢函數的概念來確定判別函數和劃分類別界面。
基本思想
假設要劃分屬于兩種類別ω1和ω2的模式樣本，這些樣本可看成是分布在n維模式空間中的點xk。
把屬于ω1的點比擬為某種能源點，在點上，電位達到峰值。
隨著與該點距離的增大，電位分布迅速減小，即把樣本xk附近空間x點上的電位分布，看成是一個勢函數K(x, xk)。
對于屬于ω1的樣本集群，其附近空間會形成一個“高地”，這些樣本點所處的位置就是“山頭”。
同理，用電位的幾何分布來看待屬于ω2的模式樣本，在其附近空間就形成“凹地”。
只要在兩類電位分布之間選擇合適的等高線，就可以認為是模式分類的判別函數。
3.9.1 判別函數的產生
模式分類的判別函數可由分布在模式空間中的許多樣本向量{xk, k=1,2,…且 
}的勢函數產生。
任意一個樣本所產生的勢函數以K(x, xk)表征，則判別函數d(x)可由勢函數序列K(x, x1)， K(x, x2)，…來構成，序列中的這些勢函數相應于在訓練過程中輸入機器的訓練模式樣本x1，x2，…。
在訓練狀態，模式樣本逐個輸入分類器，分類器就連續計算相應的勢函數，在第k步迭代時的積累位勢決定于在該步前所有的單獨勢函數的累加。
以K(x)表示積累位勢函數，若加入的訓練樣本xk+1是錯誤分類，則積累函數需要修改，若是正確分類，則不變。?
從勢函數可以看出，積累位勢起著判別函數的作用 當xk+1屬于ω1時，Kk(xk+1)>0；當xk+1屬于ω2時，Kk(xk+1)<0，則積累位勢不做任何修改就可用作判別函數。
由于一個模式樣本的錯誤分類可造成積累位勢在訓練時的變化，因此勢函數算法提供了確定ω1和ω2兩類判別函數的迭代過程。
3.9.2 勢函數的選擇
選擇勢函數的條件：一般來說，若兩個n維向量x和xk的函數K(x, xk)同時滿足下列三個條件，則可作為勢函數。
（1）K(x, xk)= K(xk, x)，并且當且僅當x=xk時達到最大值；
（2）當向量x與xk的距離趨于無窮時，K(x, xk)趨于零；
（3）K(x, xk)是光滑函數，且是x與xk之間距離的單調下降函數。
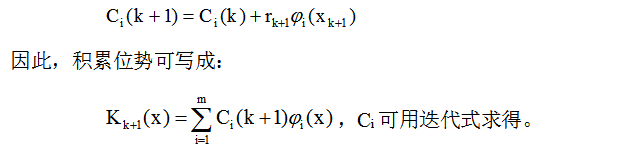
勢函數法
實例1：用第一類勢函數的算法進行分類
? ? ? ? ? ??
? ? ? ? ? ? ? ?
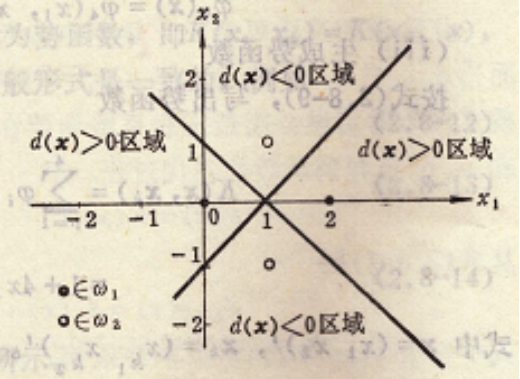
實例2：用第二類勢函數的算法進行分類
?
? ? ? ??
? ? ? ? 
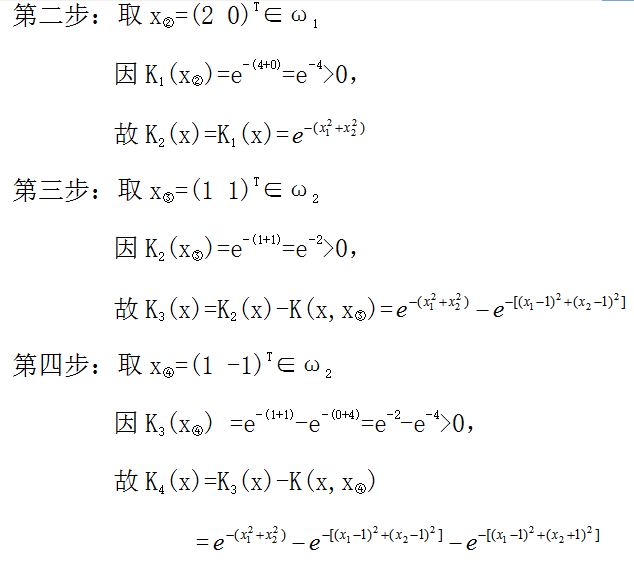
討論
用第二類勢函數，當訓練樣本維數和數目都較高時，需要計算和存儲的指數項較多。 正因為勢函數由許多新項組成，因此有很強的分類能力。
?
?
?
?
?
)
