傅里葉級數
法國數學家傅里葉發現,任何周期函數都可以用正弦函數和余弦函數構成的無窮級數來表示(選擇正弦函數與余弦函數作為基函數是因為它們是正交的),后世稱為傅里葉級數(法語:série de Fourier,或譯為傅里葉級數)。傅里葉級數在數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學等領域都有著廣泛的應用。
目錄
|
傅里葉級數的公式
給定一個周期為T的函數x(t),那么它可以表示為無窮級數:
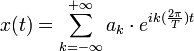 (i為虛數單位)(1)
(i為虛數單位)(1)
其中, 可以按下式計算:
可以按下式計算:
 (2)
(2)
注意到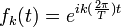 是周期為T的函數,故k 取不同值時的周期信號具有諧波關系(即它們都具有一個共同周期T)。k=0時,(1)式中對應的這一項稱為直流分量,也就是
是周期為T的函數,故k 取不同值時的周期信號具有諧波關系(即它們都具有一個共同周期T)。k=0時,(1)式中對應的這一項稱為直流分量,也就是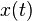 在整個周期的平均值。
在整個周期的平均值。 時具有基波頻率
時具有基波頻率 ,稱為一次諧波或基波,類似的有二次諧波,三次諧波等等。
,稱為一次諧波或基波,類似的有二次諧波,三次諧波等等。
傅里葉級數的收斂性
至今還沒有判斷傅里葉級數的收斂性充分必要條件,但是對于實際問題中出現的函數,有很多種判別條件可用于判斷收斂性。比如x(t)的可微性或級數的一致收斂性。在閉區間上滿足狄利赫里條件的函數表示成的傅里葉級數都收斂。狄利赫里條件如下:
- 在定義區間上,x(t)須絕對可積;
- 在任一有限區間中,x(t)只能取有限個極值點;
- 在任何有限區間上,x(t)只能有有限個第一類間斷點。
事實上,傅立葉級數在第一類間斷點上收斂于初始函數左右極限的算術平均值。
1966年,里納特·卡爾松證明了勒貝格二次可積函數的傅立葉級數一定是幾乎處處收斂的,即級數在除了一個可數點集外均收斂。
吉布斯現象:在x(t)的不可導點上,如果我們只取(1)式右邊的無窮級數中的有限項作和X(t),那么X(t)在這些點上會有起伏。一個簡單的例子是方波信號。
三角函數族的正交性
所謂的兩個不同向量正交是指它們的內積為0,這也就意味著這兩個向量之間沒有任何相關性,例如,在三維歐氏空間中,互相垂直的向量之間是正交的。事實上,正交是垂直在數學上的的一種抽象化和一般化。一組n個互相正交的向量必然是線性無關的,所以必然可以張成一個n維空間,也就是說,空間中的任何一個向量可以用它們來線性表出。三角函數族的正交性用公式表示出來就是:
奇函數和偶函數
奇函數 可以表示為正弦級數:
可以表示為正弦級數:
傅里葉級數的一些例子
參閱
- 離散時間傅里葉級數
- 傅里葉變換
- 維爾斯特拉斯逼近定理


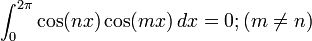











)



操作與拖放行為(DragBehavior))




的區別)
