題號1.?兩數之和:
給定一個整數數組 nums?和一個目標值 target,請你在該數組中找出和為目標值的那?兩個?整數,并返回他們的數組下標。
你可以假設每種輸入只會對應一個答案。但是,你不能重復利用這個數組中同樣的元素。
示例:
給定 nums = [2, 7, 11, 15], target = 9
因為 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
才拿到這道題時,第一個反應是遍歷每個元素 x,并查找是否存在一個值與 target?x 相等的目標元素的暴力解法,時間復雜度為O(n2),C++實現如下:
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {vector<int> ret;for (int i = 0; i < nums.size(); i++){for(int j = i + 1; j < nums.size(); j++){if(nums[i] == target - nums[j]){ret.push_back(i);ret.push_back(j);return ret;} }}ret.push_back(-1);ret.push_back(-1);return ret;}
};?
系統耗時顯示是164ms,?對于每個元素,我們試圖通過遍歷數組的其余部分來尋找它所對應的目標元素,這將耗費?O(n)?的時間。因此時間復雜度為?O(n^2),空間復雜度為O(1)。
?
為了對運行時間復雜度進行優化,我們需要一種更有效的方法來檢查數組中是否存在目標元素。如果存在,我們需要找出它的索引。保持數組中的每個元素與其索引相互對應的最好方法是什么?哈希表。
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target){unordered_map<int, int> hm1;for (int i = 0; i < nums.size(); ++i) {int complement = target - nums[i];if(hm1.find(complement) != hm1.end()){return vector<int>{hm1.find(complement)->second, i};}hm1[nums[i]] = i;}return vector<int>{-1, -1};}
};時間立馬縮減到了8ms,性能的提升是立竿見影的,但是看了標準答案,看到有位大神居然將耗時縮減到了4ms,這里附上他的解法:
static const auto io_sync_off = []()
{// turn off syncstd::ios::sync_with_stdio(false);// untie in/out streamsstd::cin.tie(nullptr);return nullptr;
}();class Solution {
public:vector<int> twoSum(vector<int>& nums, int target){map<int, int> hm1;for (int i = 0; i < nums.size(); ++i) {int complement = target - nums[i];if(hm1.find(complement) != hm1.end()){return vector<int>{hm1.find(complement)->second, i};}hm1[nums[i]] = i;}return vector<int>{-1, -1};}
};看完特地查了下開頭的函數,詳細的解釋在下面:https://blog.csdn.net/qq_32320399/article/details/81518476
https://blog.csdn.net/YinJianxiang/article/details/76436089
在ACM里,經常出現數據集超大造成 cin TLE的情況。這時候大部分人(包括原來我也是)認為這是cin的效率不及scanf的錯,甚至還上升到C語言和C++語言的執行效率層面的無聊爭論。其實像上文所說,這只是C++為了兼容而采取的保守措施。我們可以在IO之前將stdio解除綁定,這樣做了之后要注意不要同時混用cout和printf之類。
在默認的情況下cin綁定的是cout,每次執行 << 操作符的時候都要調用flush,這樣會增加IO負擔。可以通過tie(0)(0表示NULL)來解除cin與cout的綁定,進一步加快執行效率。
題號4. 尋找兩個有序數組的中位數:
給定兩個大小為 m 和 n 的有序數組?nums1?和?nums2。
請你找出這兩個有序數組的中位數,并且要求算法的時間復雜度為?O(log(m + n))。
你可以假設?nums1?和?nums2?不會同時為空。
示例 1:
nums1 = [1, 3]
nums2 = [2]則中位數是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]則中位數是 (2 + 3)/2 = 2.5
我的思路是類似二路歸并排序,但是不需要新的數組來存放兩個數組的數據,也不需要將所有數據全部排序,只需要取到中間兩個數。首先計算出總個數,然后求出中間兩個數的下標 m 和 n ,定義兩個指針,分別從兩個數組的左邊開始向后推進,知道遍歷到第 m 個和第 n 個,求出兩數的平均數并返回。當然這里同樣解除了 IO 的同步用于提升性能。
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2)
{int size = nums1.size() + nums2.size();int m = 0, n = 0;// 判斷中位數是兩數平均值還是單個值if (size % 2 == 1) // 總個數為基數則為中間值{n = size / 2;m = n;}else // 偶數則為中間倆個數的平均值{n = size / 2;m = n - 1;}double midData = 0;int leftPoint = 0;int rightPoint = 0;// 獲取中位數for (int i = 0; i <= n; ++i){// 對數組進行判斷是否越界if ( leftPoint >= nums1.size() ) // 即將進行的操作下標將越界{if (midData == 0)midData = ( (double)( nums2[m - leftPoint] + nums2[n - leftPoint] ) ) / 2;elsemidData = ( midData + nums2[n - leftPoint] ) / 2;return midData;}if ( rightPoint >= nums2.size() ) // 即將進行的操作下標將越界{if (midData == 0)midData = ( (double)( nums1[m - rightPoint] + nums1[n - rightPoint] ) ) / 2;elsemidData = ( midData + nums1[n - rightPoint] ) / 2;return midData;}// 向后推進if (nums1[leftPoint] <= nums2[rightPoint]){if (i == m)midData = (double)nums1[leftPoint];if (i == n){midData = ( midData + nums1[leftPoint] ) / 2;return midData;}leftPoint++;} else{if (i == m)midData = (double)nums2[rightPoint];if (i == n){midData = ( midData + nums2[rightPoint] ) / 2;return midData;}rightPoint++;}}return midData;
}這里出現了一個很奇怪的事情,我的方法在leetcode上顯示的時間耗時是32ms,我采用16ms的方法,提交之后還是顯示的32ms,于是我在自己電腦上寫了測試用例計算耗時:
#include <iostream>
#include <windows.h>
#include <vector>
#include <unordered_map>using namespace std;// 關閉 IO 同步
static const auto io_sync_off = []()
{// turn off syncstd::ios::sync_with_stdio(false);// untie in/out streamsstd::cin.tie(nullptr);return nullptr;
}();double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2)
{int size = 0;if(nums1.size() != 0 || nums2.size() != 0){size = nums1.size() + nums2.size();}else{return false;}int m = 0, n = 0;// 判斷中位數是兩數平均值還是單個值if (size % 2 == 1) // 總個數為基數則為中間值{n = size / 2;m = n;}else // 偶數則為中間倆個數的平均值{n = size / 2;m = n - 1;}double midData = 0;int leftPoint = 0;int rightPoint = 0;// 獲取中位數for (int i = 0; i <= n; ++i){// 對數組進行判斷是否越界if ( leftPoint >= nums1.size() ) // 即將進行的操作下標將越界{if (midData == 0)midData = ( (double)( nums2[m - leftPoint] + nums2[n - leftPoint] ) ) / 2;elsemidData = ( midData + nums2[n - leftPoint] ) / 2;return midData;}if ( rightPoint >= nums2.size() ) // 即將進行的操作下標將越界{if (midData == 0)midData = ( (double)( nums1[m - rightPoint] + nums1[n - rightPoint] ) ) / 2;elsemidData = ( midData + nums1[n - rightPoint] ) / 2;return midData;}// 向后推進if (nums1[leftPoint] <= nums2[rightPoint]){if (i == m)midData = (double)nums1[leftPoint];if (i == n){midData = ( midData + nums1[leftPoint] ) / 2;return midData;}leftPoint++;} else{if (i == m)midData = (double)nums2[rightPoint];if (i == n){midData = ( midData + nums2[rightPoint] ) / 2;return midData;}rightPoint++;}}return midData;
}// 性能最優解法
int findKth(vector<int> nums1, vector<int> nums2, int k)
{if (nums1.empty()) return nums2[k - 1];if (nums2.empty()) return nums1[k - 1];if (k == 1) return min(nums1[0], nums2[0]);int i = min((int)nums1.size(), k / 2), j = min((int)nums2.size(), k / 2);if (nums1[i - 1] > nums2[j - 1]) {return findKth(nums1, vector<int>(nums2.begin() + j, nums2.end()), k - j);} else {return findKth(vector<int>(nums1.begin() + i, nums1.end()), nums2, k - i);}return 0;
}double findMedianSortedArrays2(vector<int>& nums1, vector<int>& nums2)
{int m = nums1.size(), n = nums2.size();return (findKth(nums1, nums2, (m + n + 1) / 2) + findKth(nums1, nums2, (m + n + 2) / 2)) / 2.0;
}int main()
{struct timespec startTime,endTime;// 題號 4 測試用例
#if 1clock_gettime(CLOCK_MONOTONIC, &startTime);vector<int> vector1;vector<int> vector2;vector1.push_back(1);vector1.push_back(2);vector2.push_back(4);vector2.push_back(6);clock_gettime(CLOCK_MONOTONIC, &endTime);cout << "pushIn vector time cost :" << endTime.tv_nsec - startTime.tv_nsec << " ns" << endl;// my methodclock_gettime(CLOCK_MONOTONIC, &startTime);for (int i = 0; i < 10; ++i)findMedianSortedArrays(vector1,vector2);clock_gettime(CLOCK_MONOTONIC, &endTime);cout << "my function time cost :" << endTime.tv_nsec - startTime.tv_nsec << "ns" << endl;// 最佳方法clock_gettime(CLOCK_MONOTONIC, &startTime);for (int i = 0; i < 10; ++i)findMedianSortedArrays2(vector1,vector2);clock_gettime(CLOCK_MONOTONIC, &endTime);cout << "best function time cost :" << endTime.tv_nsec - startTime.tv_nsec << "ns" << endl;
#endifreturn 0;
}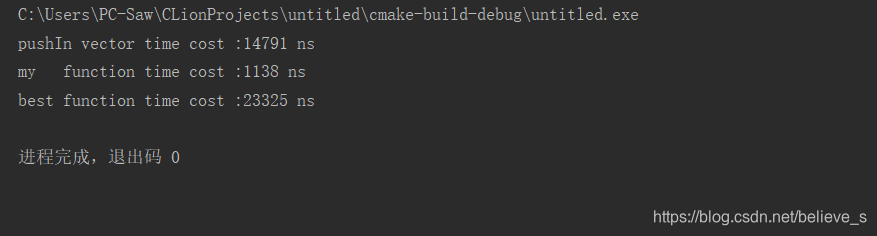
我的電腦上函數運行10次耗時如圖所示。



)















