復矩陣與共軛轉置矩陣乘積及其平方根矩陣

設 $\mathbf{A}$ 是一個 $\mathbf{m \times n}$ ?的復數矩陣，其共軛轉置矩陣（Hermitian 共軛）記為 $\mathbf{A^*}$ ? ?（即? $\mathbf{A^{^*} = \overline{A}^T}$ ），則矩陣 $\mathbf{P = A A^{^*}}$ ?（ $\mathbf{m \times m}$ ?）和 $\mathbf{Q = A^{^*} A}$ ? （ $\mathbf{n \times n}$ ?）的性質如下文所述。

1. Hermitian 性（自共軛性）

$\mathbf{P}$ ?和 $\mathbf{Q}$ ? 都是 Hermitian 矩陣，即：

? ? ? ?? $\mathbf{P^* = (A A^{^*})^{^*} = A^{^{**}} A^{^*} = A A^{^*} = P}$

同理 $\mathbf{Q^{^*} = Q}$ ?。
這意味著它們的特征值都是實數。

2. 半正定性（Positive Semi-definiteness）

對于任意非零向量 $\mathbf{x} \in \mathbb{C}^m$ ?，有：

? ? ? ?? $\mathbf{x}^* P \mathbf{x} = \mathbf{x}^* A A^* \mathbf{x} = \| A^* \mathbf{x} \|^2 \geq 0$

因此， $\mathbf{P = A A^{^*}}$ ?是半正定矩陣（所有特征值? $\geq 0$ ? ）。同理 $\mathbf{Q = A^{^*} A}$ ?也是半正定的。

3. 秩的關系

$\text{rank}(P) = \text{rank}(Q) = \text{rank}(A)$
即 $P$ ?和 $Q$ ?的秩等于 $A$ ?的秩。

4. 特征值的非負性

由于 $P$ ?和 $Q$ ?是半正定的，它們的特征值都是非負實數。此外：

$P$ ?的非零特征值與 $Q$ ?的非零特征值相同（盡管維數可能不同）。

如果 $A$ ?是方陣且可逆，則 $P$ ?和 $Q$ ?是正定矩陣（所有特征值 $> 0$ ）。

5. 矩陣? $P = A A^{^*}$ ?開平方根

5.1 存在平方根矩陣

首先， $P = A A^{^*}$ ? 時， $P$ ?可以開平方根！
因為? $P$ ?是半正定 Hermitian 矩陣，它一定存在唯一的半正定平方根 $\sqrt{P}$ ?，

即：

? ? ? ?? $\sqrt{P} \cdot \sqrt{P} = P = A A^{^*}$

5.2 計算方法

5.2.1. 譜分解（對角化）

由于 $P$ ?是 Hermitian 矩陣，它可以被對角化為：

? ? ? ?? $\mathbf{P = U D U^{^*}}$

其中 $U$ ?是酉矩陣（ $U U^* = I$ ）， $D$ ?是對角矩陣，其對角元素是 $P$ ?的特征值（非負實數）。
則平方根為：

? ? ? ?? $\sqrt{P} = U \sqrt{D} U^*$

其中 $\sqrt{D}$ ?是對 $D$ ?的對角元素取算術平方根。

5.2.2.? Cholesky 分解（如果 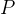$P$ ?正定）

如果 $P$ ?是正定的（即 $A$ ?是滿秩的），還可以計算 Cholesky 分解：

? ? ? ?? $P = L L^*$

其中 $L$ ?是下三角矩陣，此時 $\sqrt{P}$ ? 可以取 $L$ 。

? ? ? ? 綜上， $P = A A^{^*}$ ?是半正定 Hermitian 矩陣，其特征值非負，可以開平方根。

平方根 $\sqrt{P}$ ? 存在且唯一（如果要求半正定），可以通過譜分解或 Cholesky 分解計算。

如果 $A$ ? 是方陣且可逆，則 $P$ ?是正定的，平方根計算更簡單。

5.3 共軛轉置矩陣乘積平方根的常見應用場景

在量子力學中，密度矩陣 $\rho$ ? 滿足 $\rho = \rho^*$ ?且半正定，可以定義 $\sqrt{\rho}$ ?。在信號處理和統計學中，協方差矩陣? $\Sigma$ ?是半正定的，其平方根用于白化變換。在奇異值分解（SVD）中， $A A^*$ ? 和 $A^* A$ ?的平方根與 $A$ ?的奇異值直接相關。

重要結論

? ? ? ? 復數矩陣 $A$ ?與其共軛轉置 $A^*$ ?的乘積 $P = A A^*$ ? 總是可以開平方根，并且該平方根是唯一的半正定矩陣。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/916680.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/916680.shtml
英文地址，請注明出處：http://en.pswp.cn/news/916680.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！