對于積分區間[a, b],若
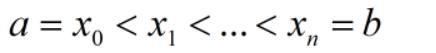
則成立
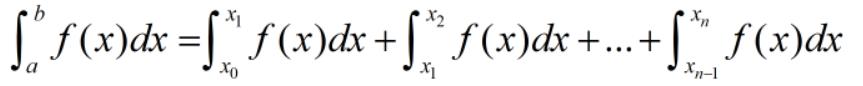
辛普森公式
辛普森公式可看作是改良的梯形公式。梯形公式是以直線逼近實際曲線,而辛普森公式則以二次曲線(即拋物線)逼近。
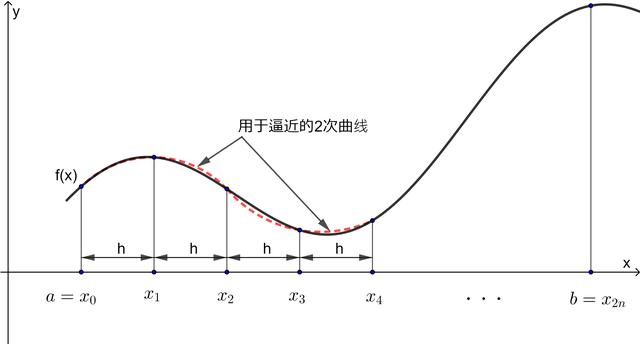
以二次曲線逼近實際曲線
根據辛普森公式可得各積分小區間內的積分值如下式所示:
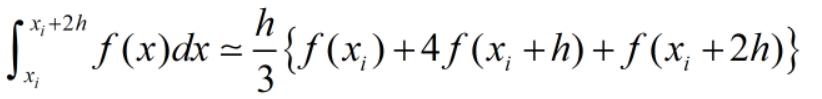
其中
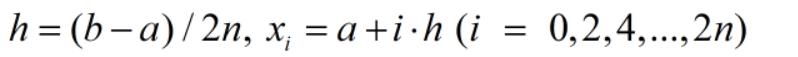
于是,全積分區間[a, b]的積分值為
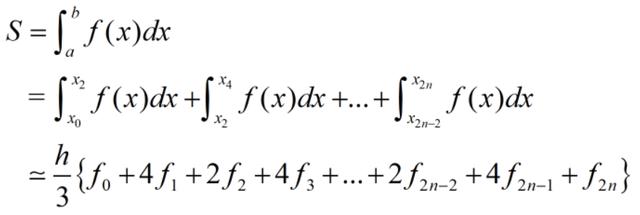
為便于計算機計算,上式可寫成
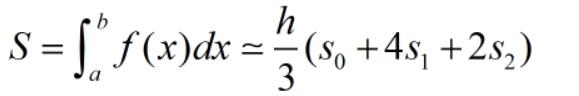
其中
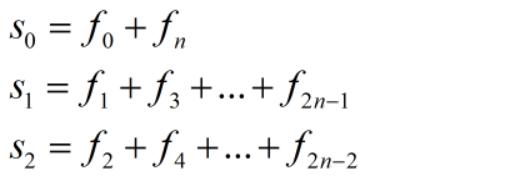
C語言程序實現辛普森公式計算積分
- 計算積分
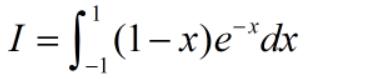
- 代碼
//simpson.c
#include
#include
/*函數定義*/
double f(double x)
{
return (1.0-x)*exp(-1*x);
}
/*辛普森公式計算積分*/
double simpson(
double a, double b, int n)
{
double h = (b-a)/n;
double s0,s1=0.0,s2=0.0;
double S;
double x;
int i;
s0 = f(a) + f(b);
for( i = 1; i < n; i += 2 )
{
x = a + h * i;
s1 += f(x);
}
for( i = 2; i < n; i += 2 )
{
x = a + h * i;
s2 += f(x);
}
S = h*(s0+4*s1+2*s2)/3;
return S;
}
int main(void)
{
//積分區間[a, b]
double a = -1.0, b = 1.0;
//區間分割數
int N[5]={10,20,30,50,100};
int i = 0;
for( i = 0; i < 5; i++ )
printf("[%3d等分]積分近似值:
I = %.7lf

)









)







