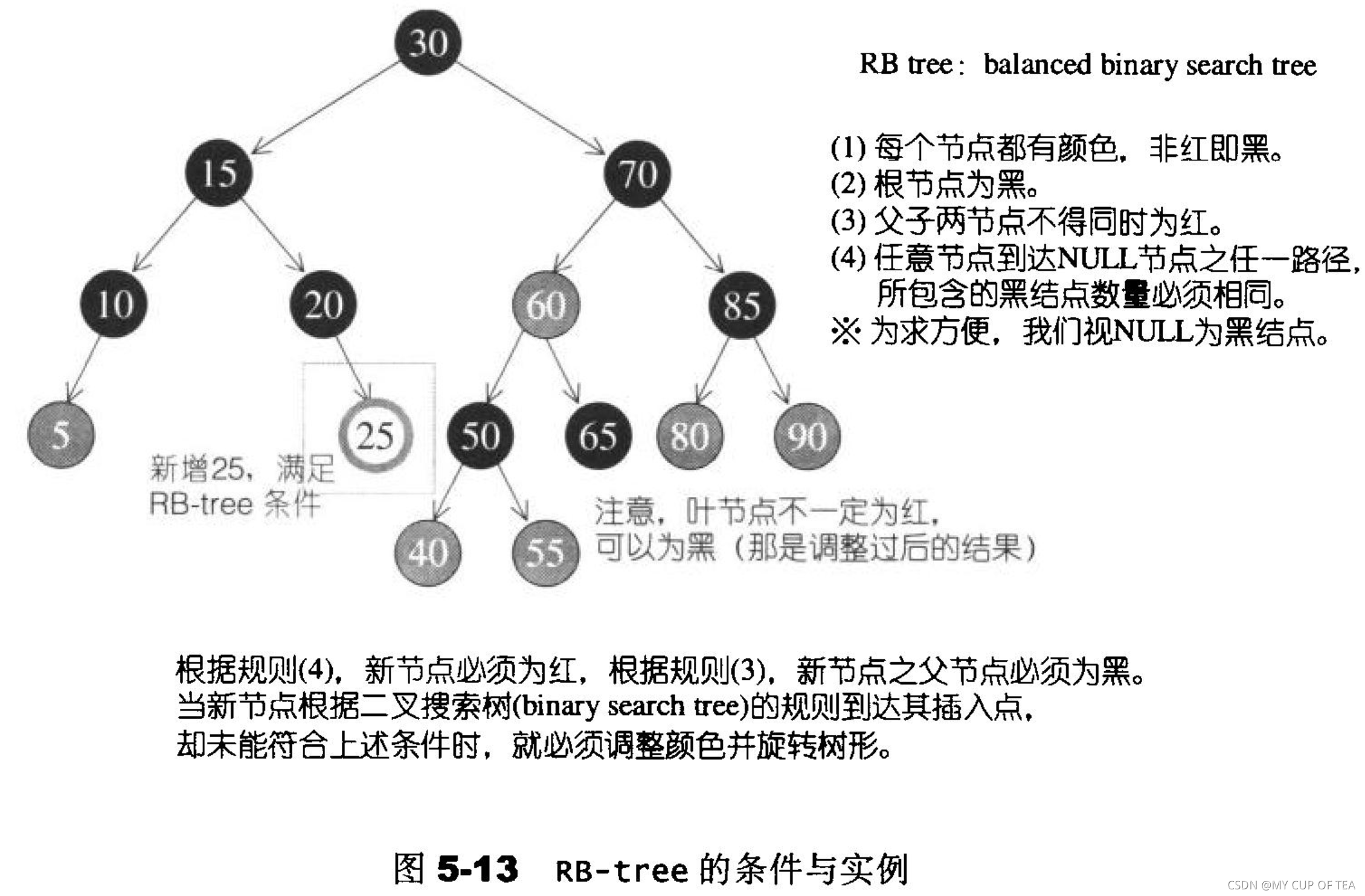
概念

• 紅黑樹不僅僅是一個二叉樹，必須滿足如下條件
• 1，每個節點不是紅色就是黑色 (深色底紋為黑色，淺色底紋為紅色)
• 2，根節點是黑色的
• 3，如果節點為紅，其子節點必須為黑色的
• 4，任一節點至NULL(樹的尾端)的任何路徑，所含的黑節點的數量必須相同

插入節點

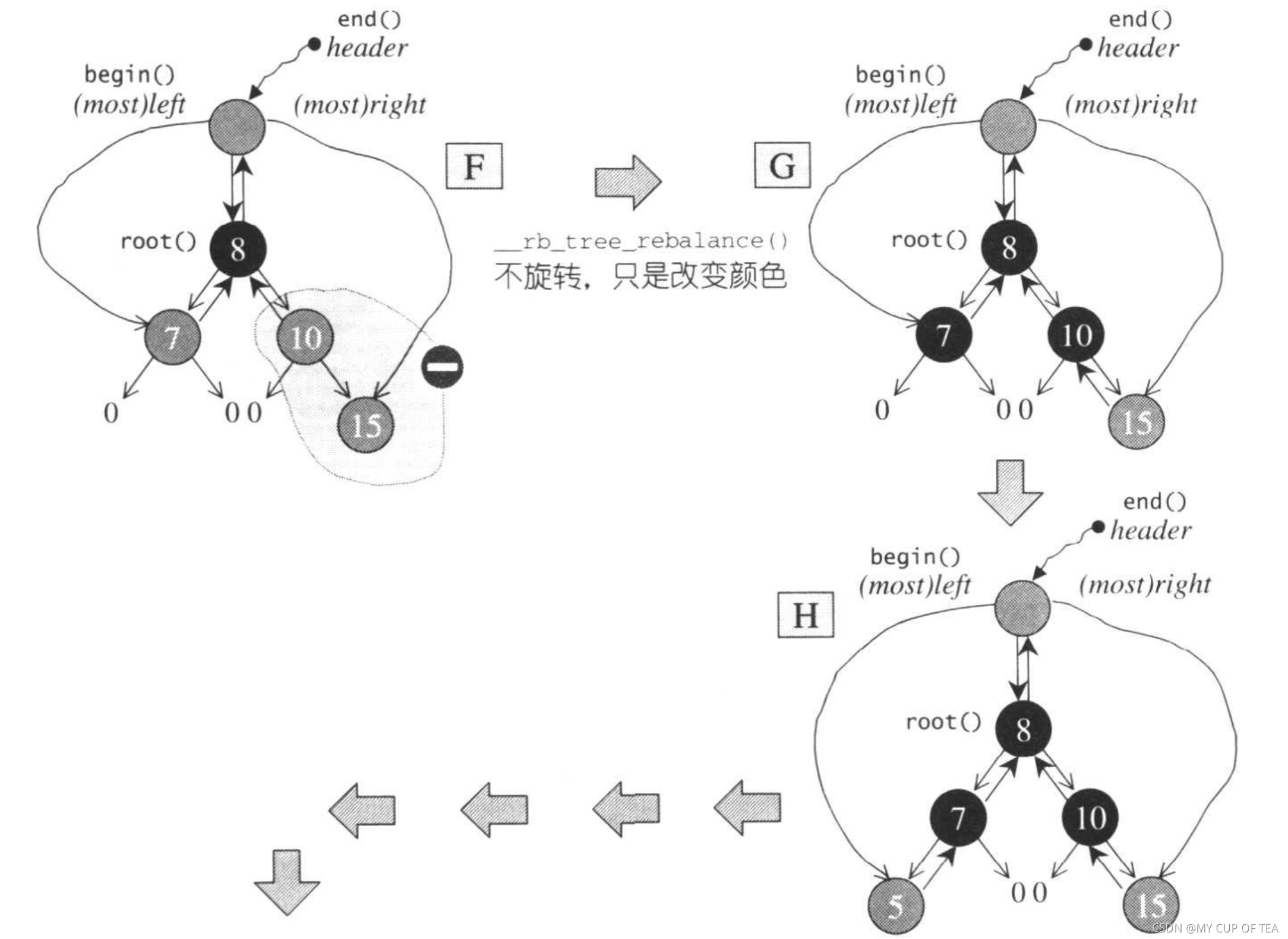
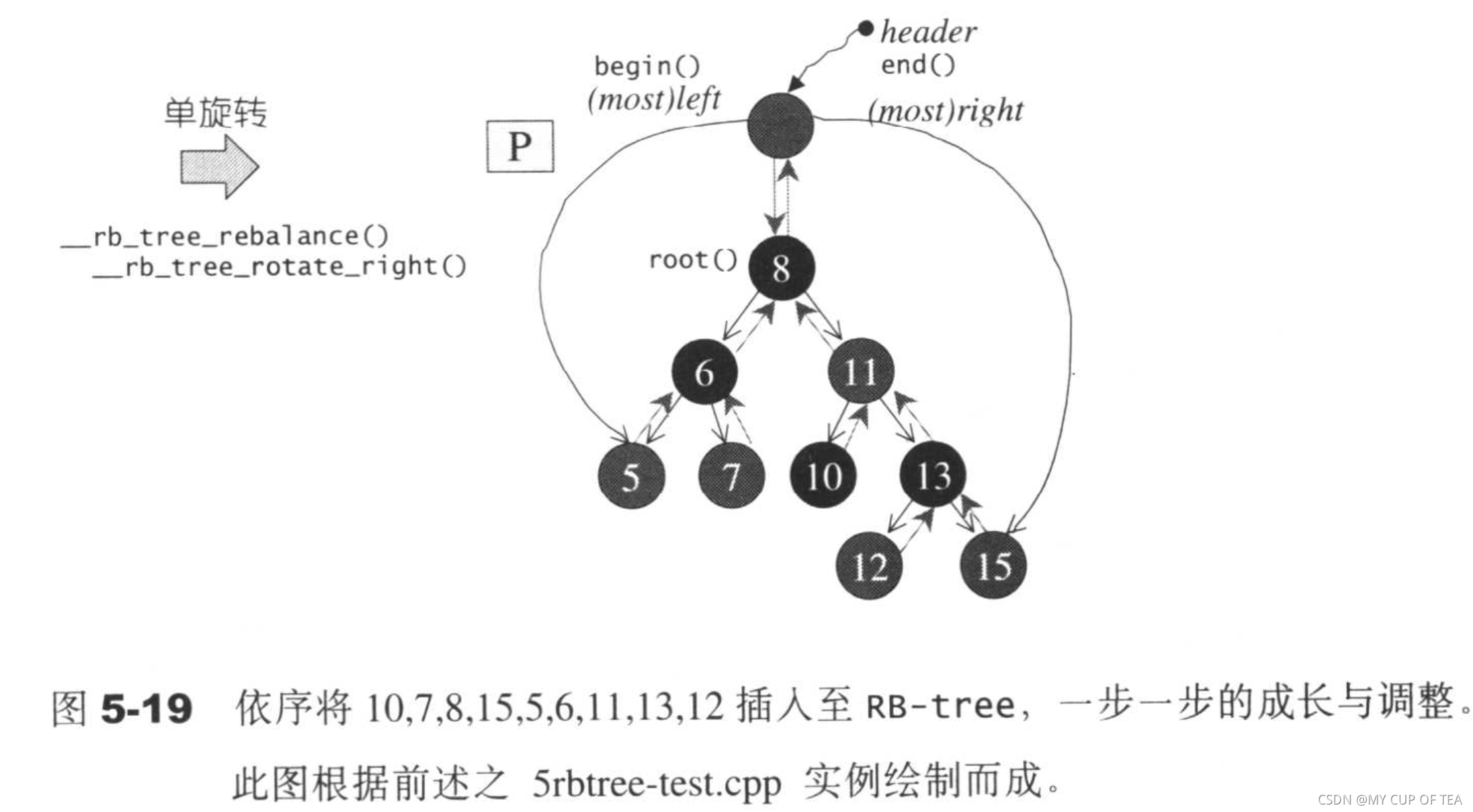
• 分別插入 3 8 35? 75 ，他們均破壞了紅黑樹的規則，需要調整樹形，兩種方式(修改顏色 或 旋轉)

?

• 產生不平衡的狀態，即高度相差1以上。這沒關系，因為RB-Tree是一種弱平衡性，他是按照顏色進行高度的限定，保證在弱平衡的前提下實現和AVL幾乎相等的搜尋效率?

?

由上而下的程序

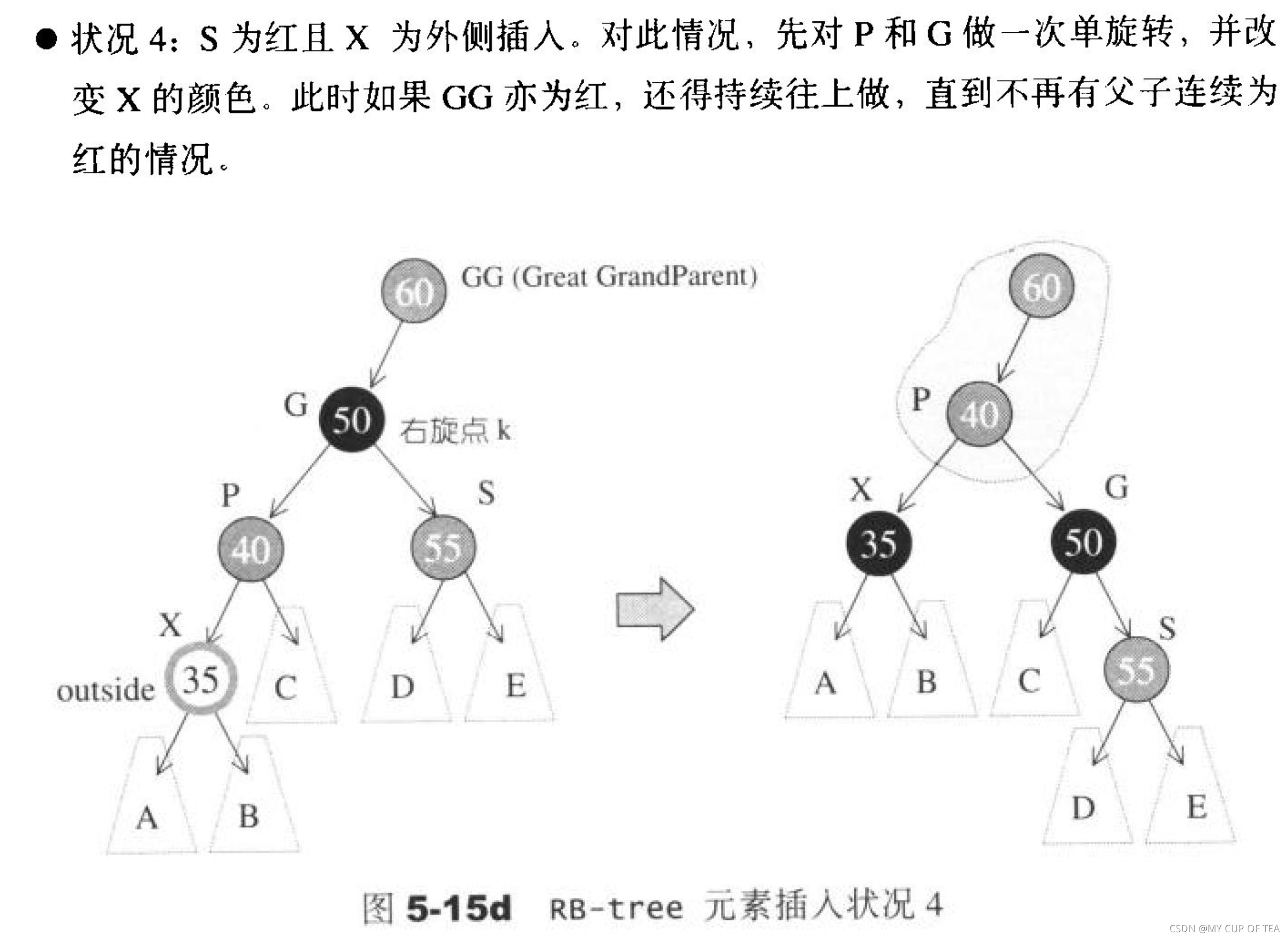
• 主要的目的是為了避免情況四 “父子節點皆為紅色的”的情形，造成了處理上時間的瓶頸
• 實現一個由上到下的程序，主要目的是檢測節點 X 的兩個孩子節點是不是紅色，如果都是紅色就將自己改為紅色，將孩子節點改為 黑色
• 如圖所示

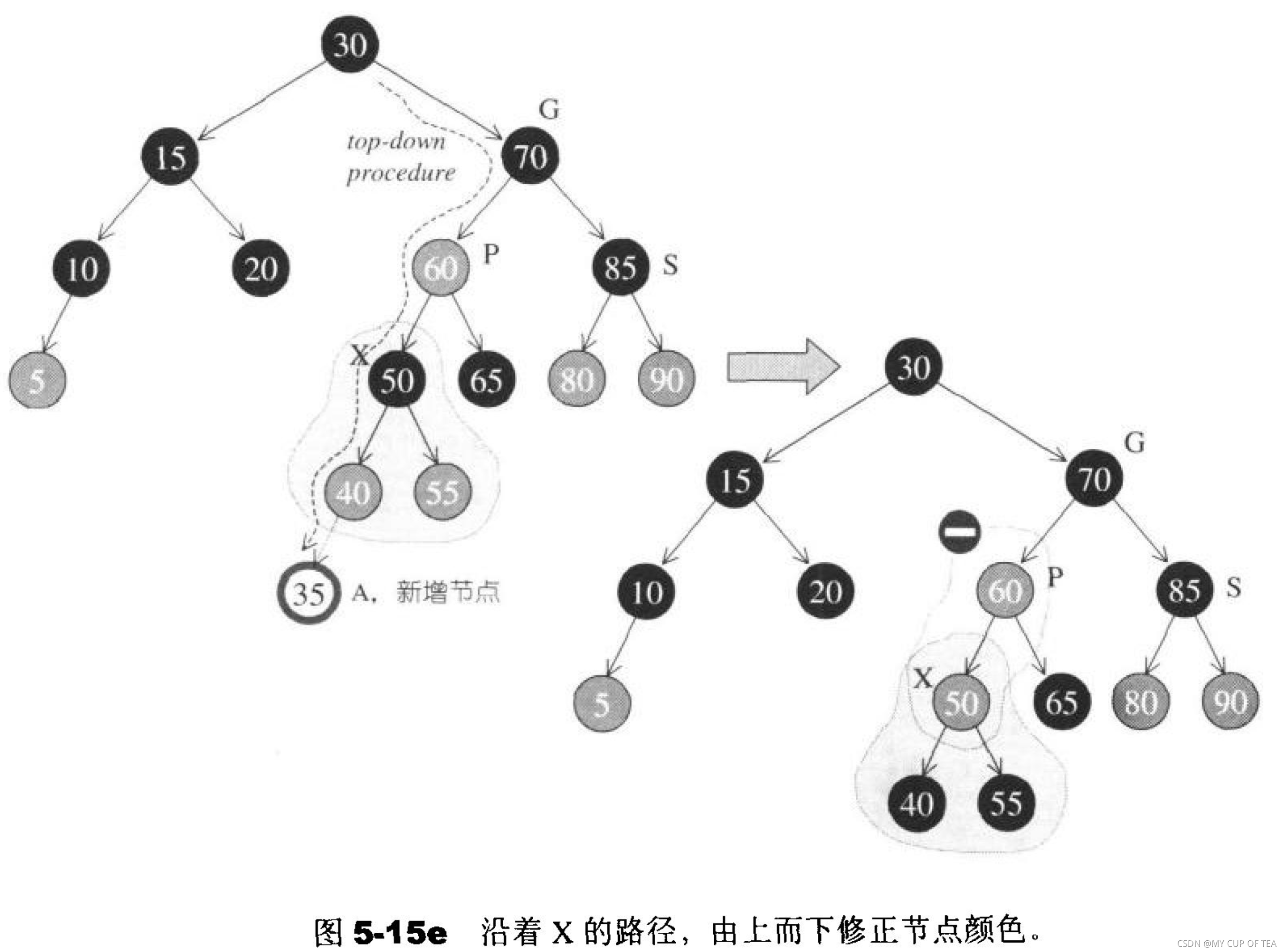
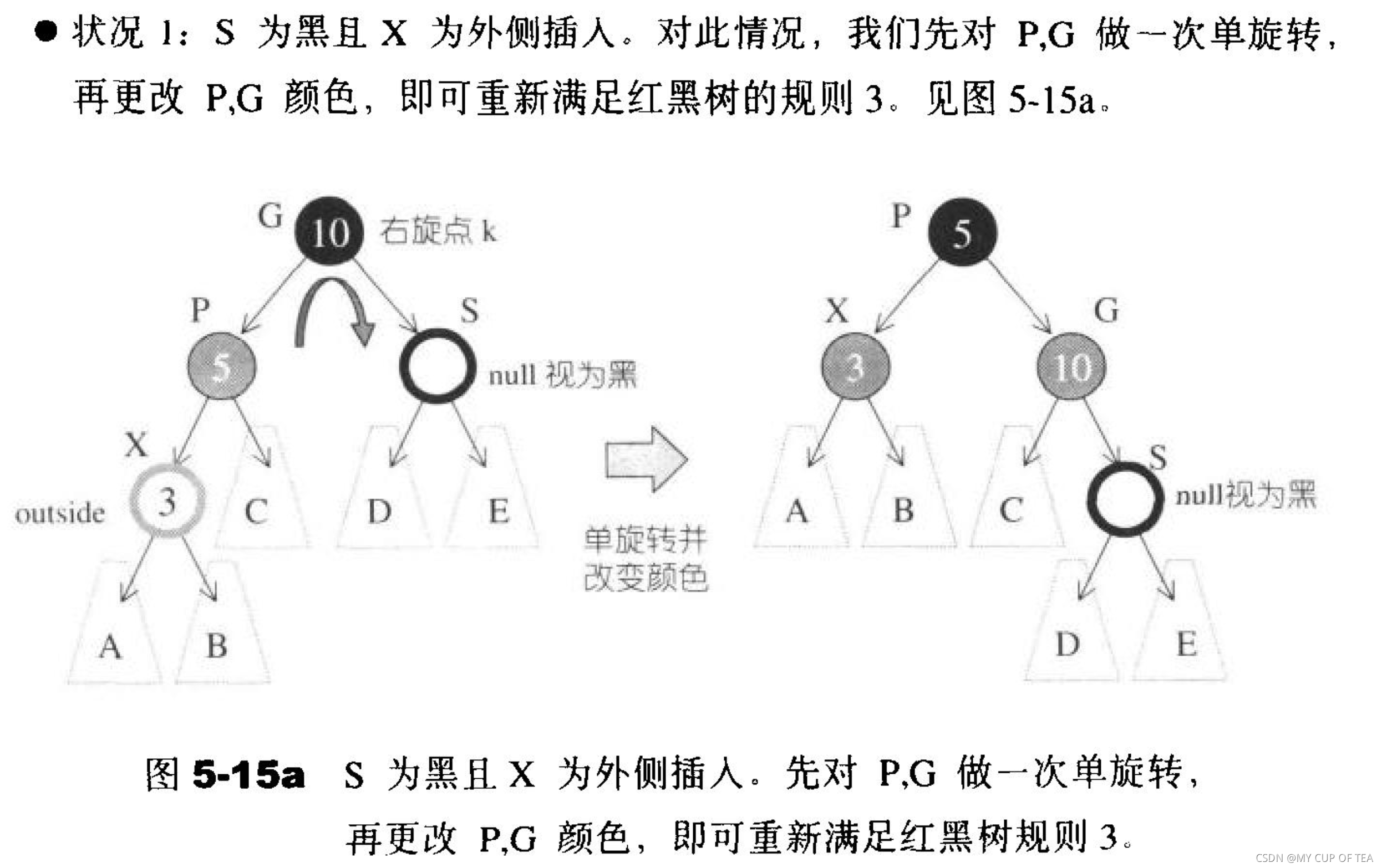
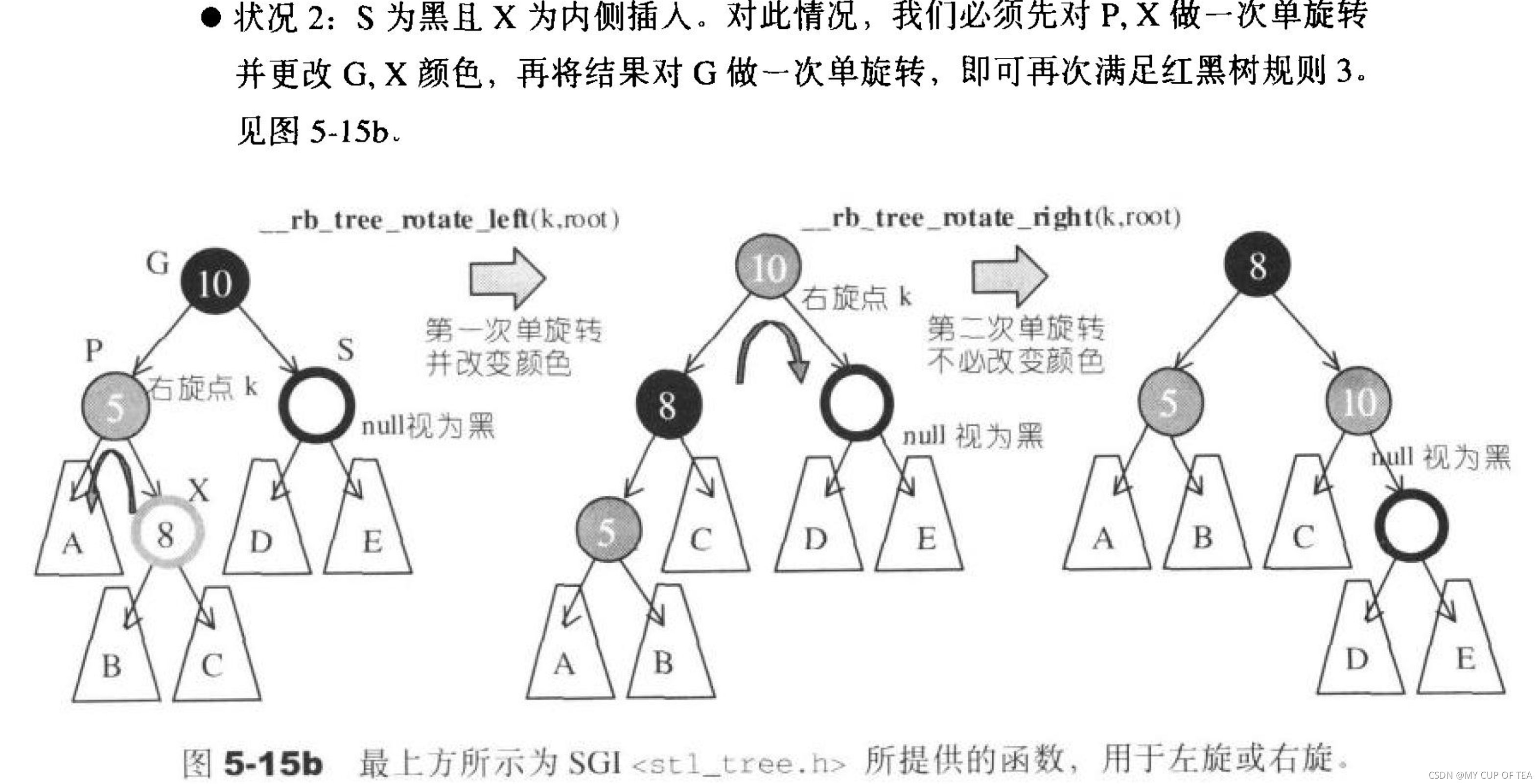
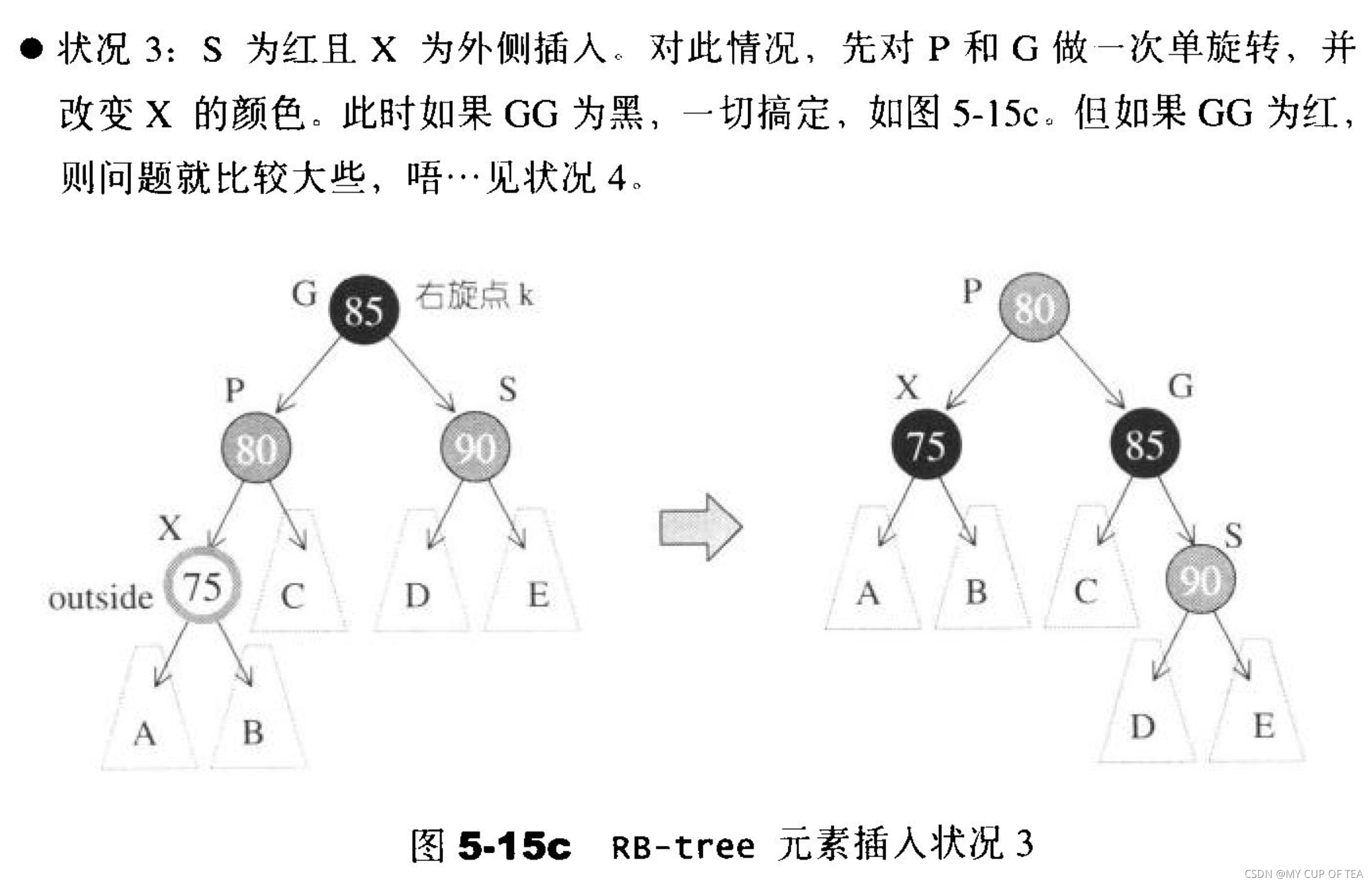
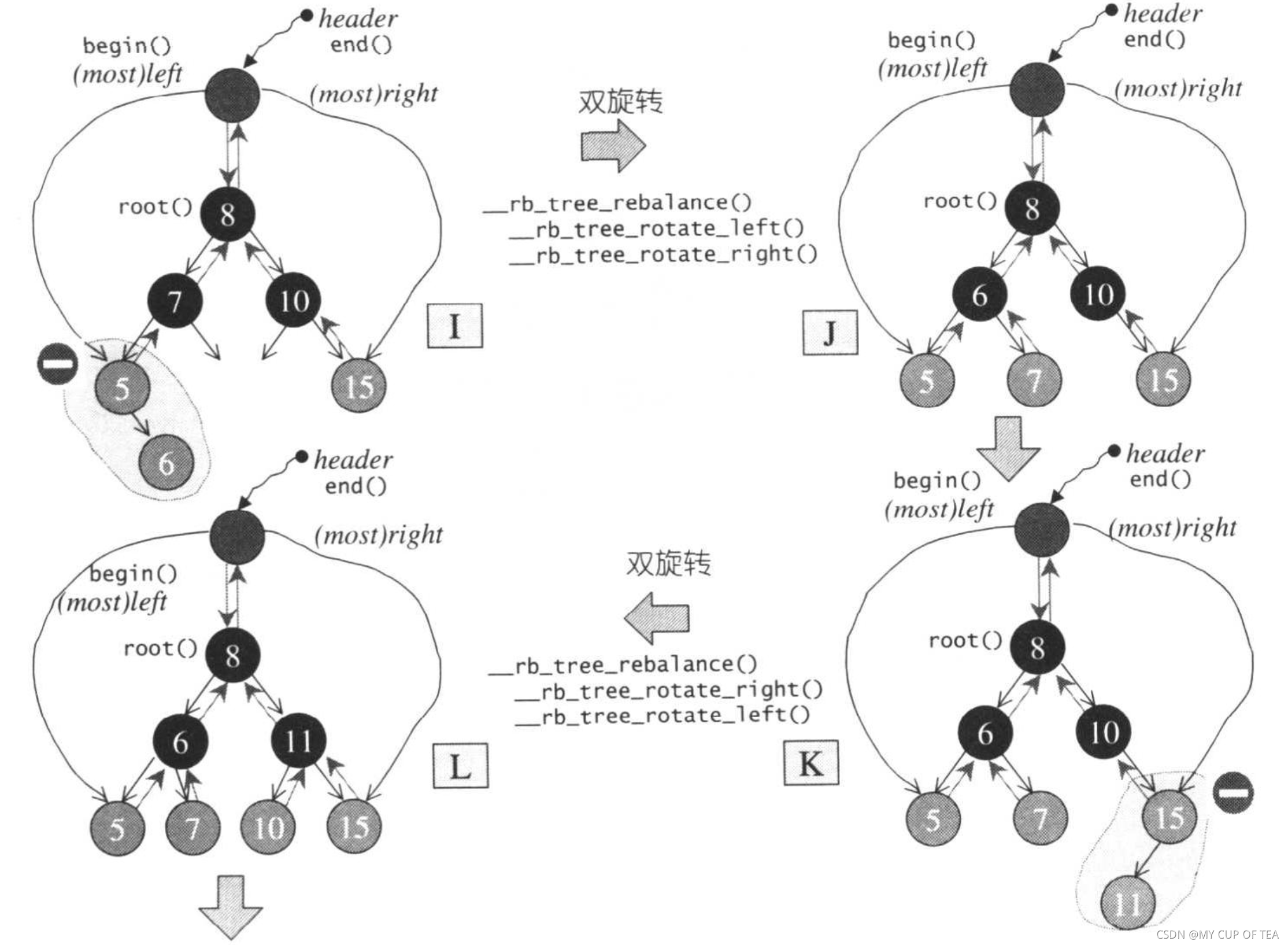
• 出現新的問題，p節點為紅色，考慮到父子節點不能同時為紅色(此時S絕對不能為紅色)，此刻就像情況一一樣需要進行一次但旋轉并改變顏色，或者做一次雙旋轉并改變顏色
• 然后 節點插入就很單純了，直接插入 或者 插入后在進行一次旋轉

RB-Tree的節點設計

• RB-tree有紅黑兩色 并且擁有左右兩個子節點
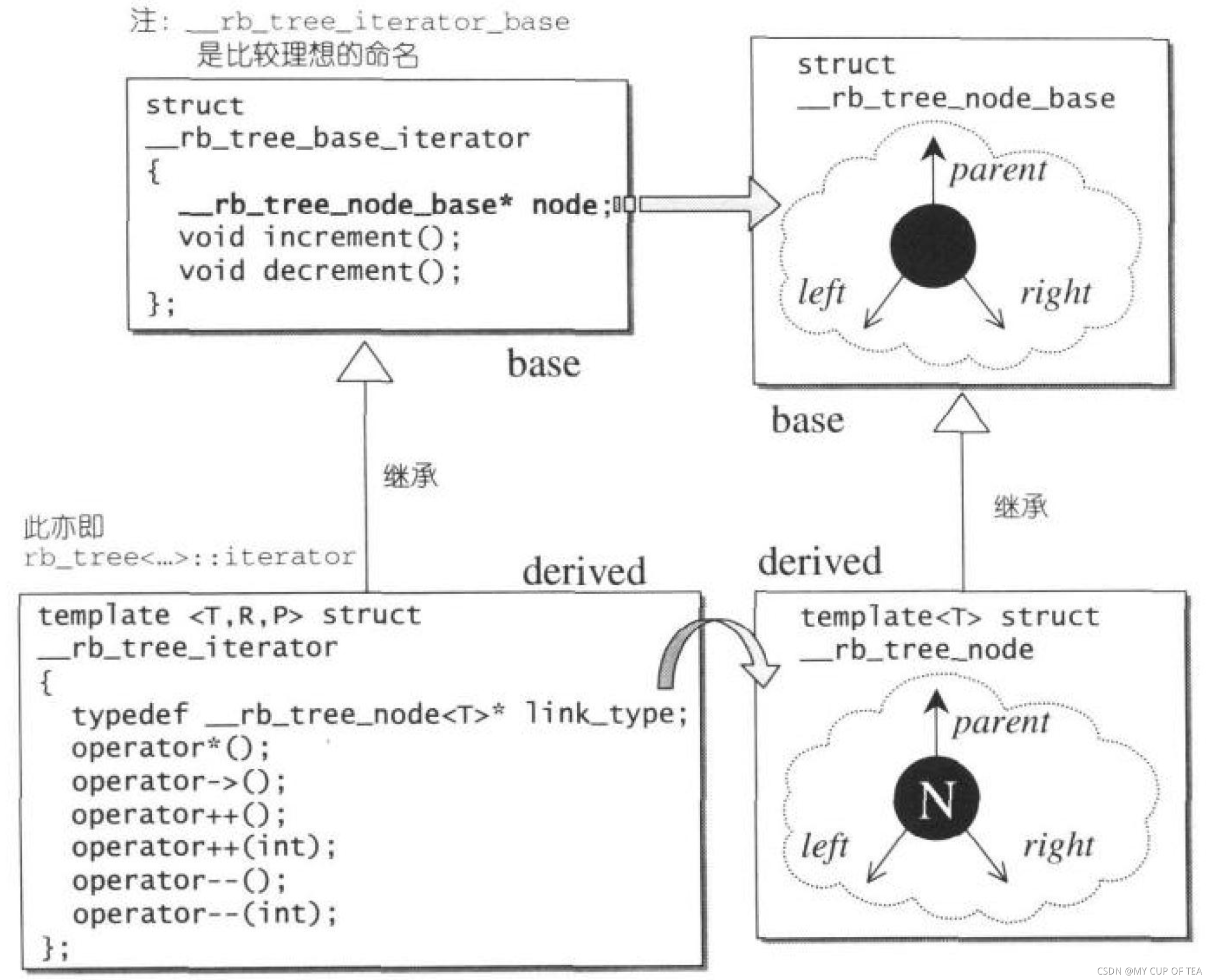
• 為了具備彈性，節點分為兩層，如圖所示節點的雙層結構和迭代器的雙層結構的關系?
• minmum() maximum()函數 可以清楚的看到RB-Tree作為一個二叉搜索樹，很方便查找極值。
• 考慮到RB-Tree各種操作需要上溯到其父節點，因此在數據結構中安排了一個parent指針

typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false;  //紅色為0
const __rb_tree_color_type __rb_tree_black = true; //黑色為1struct __rb_tree_node_base{typedef __rb_tree_color_type color_type;typedef __rb_tree_node_base* base_ptr;color_type color;   //節點顏色 非紅即黑base_ptr parent;    //RB-Tree的許多操作 都是需要父節點的參與base_ptr left;      //指向左節點base_ptr right;     //指向右節點static base_ptr minimum(base_ptr x){while (x->left != 0){//二叉搜索樹的特性//一直向左走 就會找到最小值x = x->left;}return x;}static base_ptr maximum(base_ptr x){while(x->right != 0){//二叉搜索樹的特性//一直向右走 就會找到最大值x = x->right;}return x;}
};template <class Value>
struct __rb_tree_node : public __rb_tree_node_base{typedef __rb_tree_node<Value>* link_type;Value value_field; //節點值
};

?RB-Tree的迭代器

• RB-Tree的節點和迭代器都使用struct完成，主要目的是struct默認使用public，可以被外界自由取用
• 迭代器設置為雙層結構?

• RB-Tree屬于雙向迭代器，但是不具備隨機定位的能力，其提領操作和成員訪問和list十分類似。較為特殊的是前進和后退操作。
• RB-Tree迭代器前進操作operator++ 調用了基層的increment；RB-Tree迭代器的后退操作operator--調用了基層的decrement；

//基層迭代器
struct __rb_tree_base_iterator{typedef __rb_tree_node_base::base_ptr base_ptr;typedef std::bidirectional_iterator_tag iterator_category;typedef ptrdiff_t difference_type;base_ptr node; //用于和容器之間產生一個連接關系(make a reference)//以下實現于operator++內，因為再無其他地方會調用這個函數了void increment(){if (node->right != 0){        //如果有右節點，狀況一node = node->right;       //就向右走while(node->left != 0){   //然后一直往左子樹前進node = node->left;    //即為答案}} else{                       //沒有右節點 狀況二base_ptr y = node->parent;//找出父節點while(node == y->right){  //如果現行節點本身是個右子節點node = y;             //需要一直上溯  直到不為右子節點為止y = y->parent;}if (node->right != y){    //如果此時node的右子節點不等于此時的父節點node = y;             //狀況三 此時的父節點即為解答}                         //否則 此時的node即為解答  狀況四}/*以上判斷 "若此時的右子節點不等于此時的父節點"是為了應對一種特殊的情況* 即：欲尋找的根節點的下一個節點，而此時根節點恰好沒有右子節點* 當然，上述的特殊做法需要配合RB-Tree根節點和特殊的header之間的特殊的關系*/}//以下實現于operator--內，因為再無其他地方會調用這個函數了void decrement(){//狀況一//如果是紅節點 且 父節點的父節點等于自己 右子節點即為答案//狀況一 發生于node為header的時候(亦即node為end()時)//注意：header的右子節點 即 mostright指向整棵樹的max節點if (node->color == __rb_tree_red && node->right->right == node){node = node->right;}//狀況二//如果有左子節點 令y指向左子節點；只有當y有右子節點的時候 一直往右走 到底，最后即為答案else if (node->left!=0){base_ptr y = node->left;while (y->right != 0){y = y->right;}node = y;} else{//狀況三//既不是根節點 也沒有左節點//找出父節點，當現行的節點身為左子節點時，一直交替往上走，直到現行節點不是左節點為止base_ptr y = node->parent;while(node == y->left){node = y;y = y->right;}node = y; //此時父節點即為答案}}
};//RB-Tree的正規迭代器
template <class Value,class Ref,class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator{typedef Value value_type;typedef Ref reference;typedef Ptr pointer;typedef __rb_tree_iterator<Value,Value&,Value*> iterator;typedef __rb_tree_iterator<Value,const Value&,const Value*> const_iterator;typedef __rb_tree_iterator<Value,Value&,Value*> self;typedef __rb_tree_node<Value>* link_type;__rb_tree_iterator(){}__rb_tree_iterator(link_type x){node = x;}__rb_tree_iterator(const iterator& it){node = it.node;}reference operator* () const {return link_type(node)->value_field; }#ifndef __SGI_STL_NO_ARROW_OPERATORreference operator->()const {return &(operator*());}
#endif //__SGI_STL_NO_ARROW_OPERATORself& operator++(){increment();return *this;}self operator++(int){self tmp = *this;increment();return tmp;}self& operator--(){decrement();return *this;}self operator--(int){self tmp = *this;decrement();return tmp;}};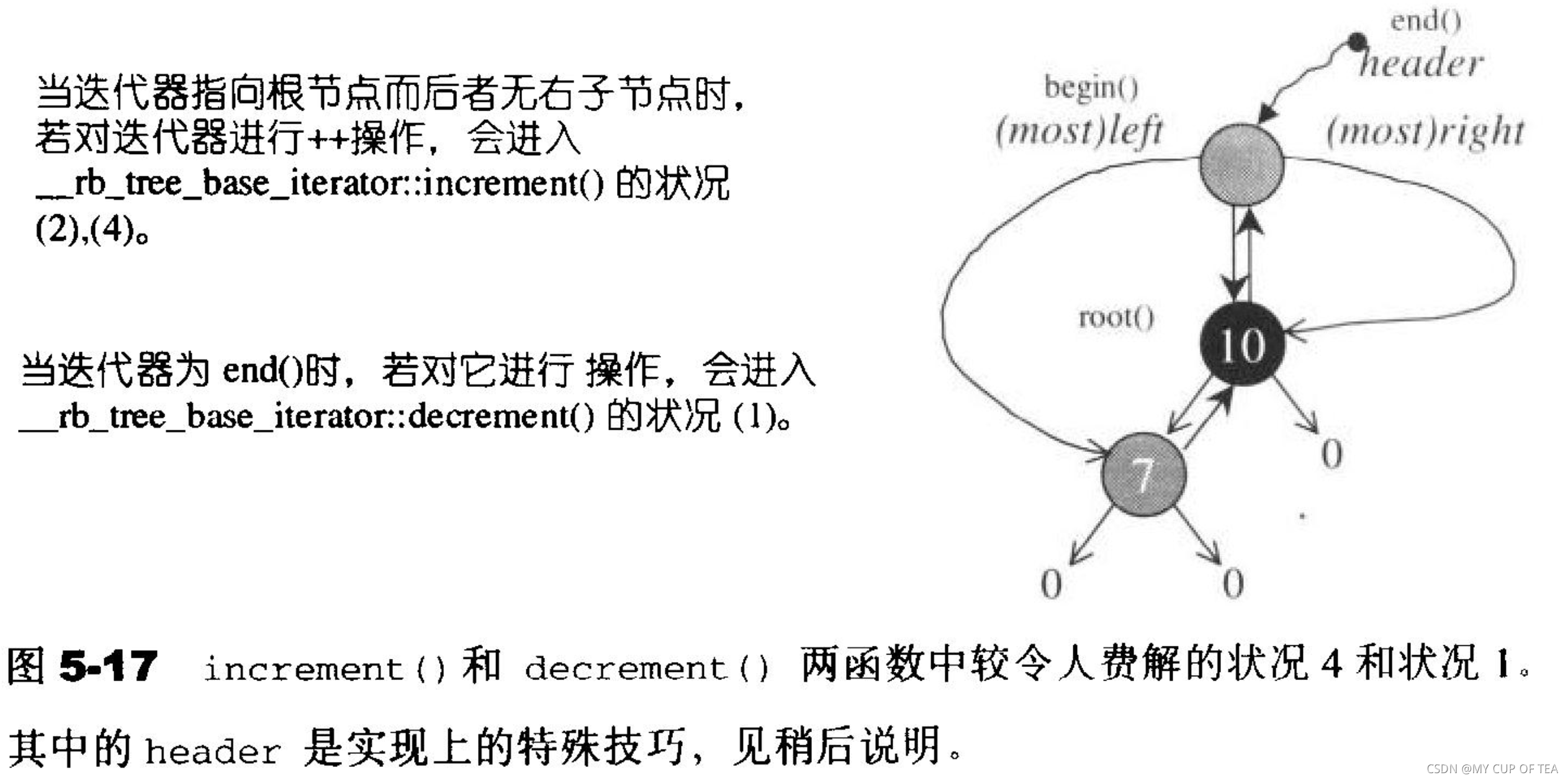

RB-tree數據結構

• 使用專屬的空間配置器，每次配置一個節點的大小
• 也可以定義各種型別的定義，用于維護RB-Tree的三筆數據
• 定義一個仿函數用于實現節點大小的比較

?

template<class T,class Alloc>
class simple_alloc{
public:static T* allocate(std::size_t n){return 0==n?0:(T*)Alloc::allocate(n * sizeof(T));}static T* allocate(void){return (T*)Alloc::allocate(sizeof (T));}static void deallocate(T* p,size_t n){if (n!=0){Alloc::deallocate(p,n * sizeof(T));}}static void deallocate(T* p){Alloc::deallocate(p,sizeof(T));}
};namespace Chy{template <class T>inline T* _allocate(ptrdiff_t size,T*){std::set_new_handler(0);T* tmp = (T*)(::operator new((std::size_t)(size * sizeof (T))));if (tmp == 0){std::cerr << "out of memory" << std::endl;exit(1);}return tmp;}template<class T>inline void _deallocate(T* buffer){::operator delete (buffer);}template<class T1,class T2>inline void _construct(T1 *p,const T2& value){new(p) T1 (value);  //沒看懂}template <class T>inline void _destroy(T* ptr){ptr->~T();}template <class T>class allocator{public:typedef T           value_type;typedef T*          pointer;typedef const T*    const_pointer;typedef T&          reference;typedef const T&    const_reference;typedef std::size_t size_type;typedef ptrdiff_t   difference_type;template<class U>struct rebind{typedef allocator<U>other;};pointer allocate(size_type n,const void * hint = 0){return _allocate((difference_type)n,(pointer)0);}void deallocate(pointer p,size_type n){_deallocate(p);}void construct(pointer p,const T& value){_construct(p,value);}void destroy(pointer p){_destroy(p);}pointer address(reference x){return (pointer)&x;}const_pointer const_address(const_reference x){return (const_pointer)&x;}size_type max_size()const{return size_type(UINT_MAX/sizeof (T));}};
}template <class Key,class Value,class KeyOfValue,class Compare,class Alloc>
class rb_tree{
protected:typedef void* void_pointer;typedef __rb_tree_node_base* base_ptr;typedef __rb_tree_node<Value> rb_tree_node;typedef simple_alloc<rb_tree_node,Alloc>rb_tree_node_allocator;typedef __rb_tree_color_type color_type;
public:typedef Key key_type;typedef Value value_type;typedef value_type* pointer;typedef const value_type* const_pointer;typedef value_type& reference;typedef const value_type& const_reference;typedef rb_tree_node* link_type;typedef std::size_t size_type;typedef std::ptrdiff_t difference_type;
protected:link_type get_node(){return rb_tree_node_allocator::allocate();}void put_node(link_type p){return rb_tree_node_allocator::deallocate(p);}link_type create_node(const value_type& x){link_type tmp = get_node(); //配置空間__STL_TRY{Chy::allocator<Key>::construct(&tmp->value_field,x);//構造內容};__STL_UNWIND(put_node(tmp));return tmp;}link_type clone_node(link_type x){//復制一個節點的顏色和數值link_type tmp = create_node(x->value_field);tmp->color = x->color;tmp->left = 0;tmp->right = 0;return tmp;}void destroy_node(link_type p){Chy::allocator<Key>::destroy(&p->value_field); //析構內容put_node(p); //釋放內存}
protected://RB-tree只使用三筆數據表現size_type node_count; //追蹤記錄樹的大小 (節點的數量)link_type header;     //實現上的小技巧Compare key_compare;  //節點之間的鍵值大小的比較準則. 應該會是一個function object//以下三個函數用于方便獲取header的成員link_type& root() const{return (link_type&)header->parent;}link_type& left_most() const{return (link_type&)header->left;}link_type& right_most() const{return (link_type&)header->right;}//以下六個函數用于方便獲得節點x的成員static link_type& left(link_type x){ return(link_type&)x->left;}static link_type& right(link_type x){ return(link_type&)x->right;}static link_type& parent(link_type x){ return(link_type&)x->parent;}static reference value(link_type x){ return x->value_field;}static const Key& key(link_type x){ return KeyOfValue()(value(x));}static color_type& color(link_type x){return (color_type&) (x->color);}//獲取極大值和極小值 node class有實現此功能static link_type minimum(link_type x){return (link_type) __rb_tree_node_base::minimum(x);}static link_type maximum(link_type x){return (link_type) __rb_tree_node_base::maximum(x);}//迭代器typedef __rb_tree_iterator<value_type,reference,pointer>iterator;
private:iterator __insert(base_ptr x,base_ptr y,const value_type& v);link_type __copy(link_type x,link_type p);void __erase(link_type x);void clear() {if (node_count != 0) {__erase(root());left_most() = header;root() = 0;right_most() = header;node_count = 0;}}void init(){header = get_node(); //產生一個節點空間 令header指向它color(header) = __rb_tree_red;//令header為紅色 用于區分header和root,在iterator的operator++中root() == 0;left_most() = header;   //令header的左子節點等于自己right_most() = header;  //令header的右子節點等于自己}
public://allocation / deallocationrb_tree(const Compare& comp = Compare()): node_count(0),key_compare(comp){init();}~rb_tree(){clear();put_node(header);}rb_tree<Key,Value,KeyOfValue,Compare,Alloc>&operator==(const rb_tree<Key,Value,KeyOfValue,Compare,Alloc>&x);
public://accessorsCompare key_comp() const {return key_compare;}iterator begin() {return left_most();} //RB樹的起頭為最左(最小)節點處iterator end(){return header;} //RB樹的終點為header所指處bool empty() const {return node_count == 0;}size_type size() const {return node_count;}size_type max_size() const {return size_type (-1);}
public://insert/erase//將x插入到RB-Tree中 (保持節點的獨一無二)std::pair<iterator,bool> insert_unique(const value_type& x);//將x插入到RB-Tree中 (允許節點數值重復)iterator insert_equal(const value_type& x);
};

RB-Tree的構造和內存管理

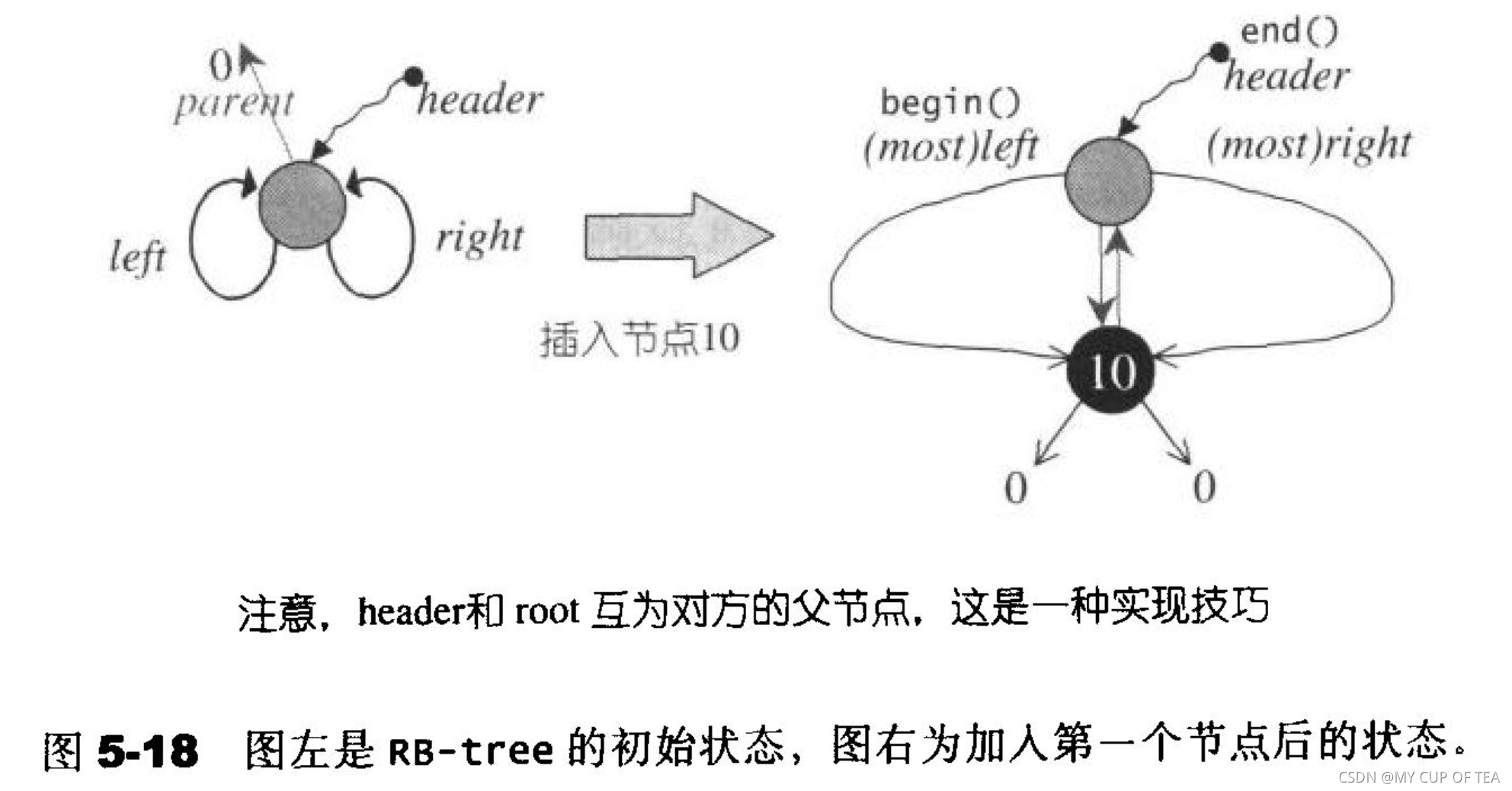
• 邊界情況的考慮，也就是走到根節點的時候需要有特殊的處理
• SGI STL為根節點載設計了一個父節點 名為header。每當插入節點的時候，不僅僅需要按照紅黑樹的規則進行調整，還需要維護header的正確性，使其父節點執行根節點，左子節點指向最小節點、右子節點指向最大節點

?RB-Tree的元素操作

• 元素的插入和搜尋。插入元素的鍵值是否可以重復作為區分
• 用戶需要明確設定所謂的KeyOfValue仿函數

?

完整代碼

#include <iostream>#ifdef __STL_USE_EXCEPTIONS
#define __STL_TRY   try
#define __STL_UNWIND(action)   catch(...) { action; throw; }
#else
#define __STL_TRY
#define __STL_UNWIND(action)
#endiftypedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false;  //紅色為0
const __rb_tree_color_type __rb_tree_black = true; //黑色為1struct __rb_tree_node_base{typedef __rb_tree_color_type color_type;typedef __rb_tree_node_base* base_ptr;color_type color;   //節點顏色 非紅即黑base_ptr parent;    //RB-Tree的許多操作 都是需要父節點的參與base_ptr left;      //指向左節點base_ptr right;     //指向右節點static base_ptr minimum(base_ptr x){while (x->left != 0){//二叉搜索樹的特性//一直向左走 就會找到最小值x = x->left;}return x;}static base_ptr maximum(base_ptr x){while(x->right != 0){//二叉搜索樹的特性//一直向右走 就會找到最大值x = x->right;}return x;}
};template <class Value>
struct __rb_tree_node : public __rb_tree_node_base{typedef __rb_tree_node<Value>* link_type;Value value_field; //節點值
};//基層迭代器
struct __rb_tree_base_iterator{typedef __rb_tree_node_base::base_ptr base_ptr;typedef std::bidirectional_iterator_tag iterator_category;typedef ptrdiff_t difference_type;base_ptr node; //用于和容器之間產生一個連接關系(make a reference)//以下實現于operator++內，因為再無其他地方會調用這個函數了void increment(){if (node->right != 0){        //如果有右節點，狀況一node = node->right;       //就向右走while(node->left != 0){   //然后一直往左子樹前進node = node->left;    //即為答案}} else{                       //沒有右節點 狀況二base_ptr y = node->parent;//找出父節點while(node == y->right){  //如果現行節點本身是個右子節點node = y;             //需要一直上溯  直到不為右子節點為止y = y->parent;}if (node->right != y){    //如果此時node的右子節點不等于此時的父節點node = y;             //狀況三 此時的父節點即為解答}                         //否則 此時的node即為解答  狀況四}/*以上判斷 "若此時的右子節點不等于此時的父節點"是為了應對一種特殊的情況* 即：欲尋找的根節點的下一個節點，而此時根節點恰好沒有右子節點* 當然，上述的特殊做法需要配合RB-Tree根節點和特殊的header之間的特殊的關系*/}//以下實現于operator--內，因為再無其他地方會調用這個函數了void decrement(){//狀況一//如果是紅節點 且 父節點的父節點等于自己 右子節點即為答案//狀況一 發生于node為header的時候(亦即node為end()時)//注意：header的右子節點 即 mostright指向整棵樹的max節點if (node->color == __rb_tree_red && node->right->right == node){node = node->right;}//狀況二//如果有左子節點 令y指向左子節點；只有當y有右子節點的時候 一直往右走 到底，最后即為答案else if (node->left!=0){base_ptr y = node->left;while (y->right != 0){y = y->right;}node = y;} else{//狀況三//既不是根節點 也沒有左節點//找出父節點，當現行的節點身為左子節點時，一直交替往上走，直到現行節點不是左節點為止base_ptr y = node->parent;while(node == y->left){node = y;y = y->right;}node = y; //此時父節點即為答案}}
};//RB-Tree的正規迭代器
template <class Value,class Ref,class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator{typedef Value value_type;typedef Ref reference;typedef Ptr pointer;typedef __rb_tree_iterator<Value,Value&,Value*> iterator;typedef __rb_tree_iterator<Value,const Value&,const Value*> const_iterator;typedef __rb_tree_iterator<Value,Value&,Value*> self;typedef __rb_tree_node<Value>* link_type;__rb_tree_iterator(){}__rb_tree_iterator(link_type x){node = x;}__rb_tree_iterator(const iterator& it){node = it.node;}reference operator* () const {return link_type(node)->value_field; }#ifndef __SGI_STL_NO_ARROW_OPERATORreference operator->()const {return &(operator*());}
#endif //__SGI_STL_NO_ARROW_OPERATORself& operator++(){increment();return *this;}self operator++(int){self tmp = *this;increment();return tmp;}self& operator--(){decrement();return *this;}self operator--(int){self tmp = *this;decrement();return tmp;}};template<class T,class Alloc>
class simple_alloc{
public:static T* allocate(std::size_t n){return 0==n?0:(T*)Alloc::allocate(n * sizeof(T));}static T* allocate(void){return (T*)Alloc::allocate(sizeof (T));}static void deallocate(T* p,size_t n){if (n!=0){Alloc::deallocate(p,n * sizeof(T));}}static void deallocate(T* p){Alloc::deallocate(p,sizeof(T));}
};namespace Chy{template <class T>inline T* _allocate(ptrdiff_t size,T*){std::set_new_handler(0);T* tmp = (T*)(::operator new((std::size_t)(size * sizeof (T))));if (tmp == 0){std::cerr << "out of memory" << std::endl;exit(1);}return tmp;}template<class T>inline void _deallocate(T* buffer){::operator delete (buffer);}template<class T1,class T2>inline void _construct(T1 *p,const T2& value){new(p) T1 (value);  //沒看懂}template <class T>inline void _destroy(T* ptr){ptr->~T();}template <class T>class allocator{public:typedef T           value_type;typedef T*          pointer;typedef const T*    const_pointer;typedef T&          reference;typedef const T&    const_reference;typedef std::size_t size_type;typedef ptrdiff_t   difference_type;template<class U>struct rebind{typedef allocator<U>other;};pointer allocate(size_type n,const void * hint = 0){return _allocate((difference_type)n,(pointer)0);}void deallocate(pointer p,size_type n){_deallocate(p);}void construct(pointer p,const T& value){_construct(p,value);}void destroy(pointer p){_destroy(p);}pointer address(reference x){return (pointer)&x;}const_pointer const_address(const_reference x){return (const_pointer)&x;}size_type max_size()const{return size_type(UINT_MAX/sizeof (T));}};
}template <class Key,class Value,class KeyOfValue,class Compare,class Alloc>
class rb_tree{
protected:typedef void* void_pointer;typedef __rb_tree_node_base* base_ptr;typedef __rb_tree_node<Value> rb_tree_node;typedef simple_alloc<rb_tree_node,Alloc>rb_tree_node_allocator;typedef __rb_tree_color_type color_type;
public:typedef Key key_type;typedef Value value_type;typedef value_type* pointer;typedef const value_type* const_pointer;typedef value_type& reference;typedef const value_type& const_reference;typedef rb_tree_node* link_type;typedef std::size_t size_type;typedef std::ptrdiff_t difference_type;
protected:link_type get_node(){return rb_tree_node_allocator::allocate();}void put_node(link_type p){return rb_tree_node_allocator::deallocate(p);}link_type create_node(const value_type& x){link_type tmp = get_node(); //配置空間__STL_TRY{Chy::allocator<Key>::construct(&tmp->value_field,x);//構造內容};__STL_UNWIND(put_node(tmp));return tmp;}link_type clone_node(link_type x){//復制一個節點的顏色和數值link_type tmp = create_node(x->value_field);tmp->color = x->color;tmp->left = 0;tmp->right = 0;return tmp;}void destroy_node(link_type p){Chy::allocator<Key>::destroy(&p->value_field); //析構內容put_node(p); //釋放內存}
protected://RB-tree只使用三筆數據表現size_type node_count; //追蹤記錄樹的大小 (節點的數量)link_type header;     //實現上的小技巧Compare key_compare;  //節點之間的鍵值大小的比較準則. 應該會是一個function object//以下三個函數用于方便獲取header的成員link_type& root() const{return (link_type&)header->parent;}link_type& left_most() const{return (link_type&)header->left;}link_type& right_most() const{return (link_type&)header->right;}//以下六個函數用于方便獲得節點x的成員static link_type& left(link_type x){ return(link_type&)x->left;}static link_type& right(link_type x){ return(link_type&)x->right;}static link_type& parent(link_type x){ return(link_type&)x->parent;}static reference value(link_type x){ return x->value_field;}static const Key& key(link_type x){ return KeyOfValue()(value(x));}static color_type& color(link_type x){return (color_type&) (x->color);}//獲取極大值和極小值 node class有實現此功能static link_type minimum(link_type x){return (link_type) __rb_tree_node_base::minimum(x);}static link_type maximum(link_type x){return (link_type) __rb_tree_node_base::maximum(x);}//迭代器typedef __rb_tree_iterator<value_type,reference,pointer>iterator;
public:iterator __insert(base_ptr x,base_ptr y,const value_type& v);link_type __copy(link_type x,link_type p);void __erase(link_type x);void clear() {if (node_count != 0) {__erase(root());left_most() = header;root() = 0;right_most() = header;node_count = 0;}}void init(){header = get_node(); //產生一個節點空間 令header指向它color(header) = __rb_tree_red;//令header為紅色 用于區分header和root,在iterator的operator++中root() == 0;left_most() = header;   //令header的左子節點等于自己right_most() = header;  //令header的右子節點等于自己}
public://allocation / deallocationrb_tree(const Compare& comp = Compare()): node_count(0),key_compare(comp){init();}~rb_tree(){clear();put_node(header);}rb_tree<Key,Value,KeyOfValue,Compare,Alloc>&operator==(const rb_tree<Key,Value,KeyOfValue,Compare,Alloc>&x);
public://accessorsCompare key_comp() const {return key_compare;}iterator begin() {return left_most();} //RB樹的起頭為最左(最小)節點處iterator end(){return header;} //RB樹的終點為header所指處bool empty() const {return node_count == 0;}size_type size() const {return node_count;}size_type max_size() const {return size_type (-1);}
public://insert/erase//將x插入到RB-Tree中 (保持節點的獨一無二)std::pair<iterator,bool> insert_unique(const value_type& x);//將x插入到RB-Tree中 (允許節點數值重復)iterator insert_equal(const value_type& x);//尋找鍵值為k的節點iterator find(const value_type& k);
};//插入新的數值 節點鍵值允許重復
//注意：返回的是一個RB-Tree的迭代器，指向的是新增的節點
template <class Key,class Value,class KeyOfValue,class Compare,class Alloc>
typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iteratorrb_tree<Key,Value,KeyOfValue,Compare,Alloc>::insert_equal(const value_type &v) {link_type y = header;link_type x = root(); //根節點開始while(x != 0){        //根節點開始 從上往下尋找適當的插入節點y = x;//如果當前根節點比 輸入的v大，則轉向左邊，否則轉向右邊x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x);}//x為新值插入點 y為插入點的父節點 v為新值return __insert(x,y,v);
}//插入新的數值 節點鍵值不允許重復
//注意：返回結果是pair類型，第一個元素是一個RB-Tree的迭代器，指向的是新增的節點；第二個參數表示插入成功與否
template <class Key,class Value,class KeyOfValue,class Compare,class Alloc>
std::pair<typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iterator,bool>
rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::insert_unique(const value_type &v) {link_type y = header;link_type x = root(); //從根節點開始bool comp = true;while(x != 0){ //從根節點開始 往下尋找適當的插入點y = x;comp = key_compare(KeyOfValue()(v), key(x)); //v鍵值小于目前節點的鍵值x = comp ? left(x) : right(x); //遇"大"則向左 遇"小"則向右}//離開while循環之后 y所指的即 插入點之父節點（此時它必為葉子結點）iterator j = iterator(y); //迭代器j指向插入點的父節點yif (comp){//如果while循環時候，判定comp的數值，如果comp為真(表示遇到大的元素，將插入左側)//如果插入節點的父節點是最左側的節點//x為插入點，y為插入節點的父節點，v表示新值if (j == begin()){return std::pair<iterator,bool>(__insert(x,y,v), true);} else{//插入節點的父節點不是最左側的節點//調整j 回頭準備測試--j;}if (key_compare(key(j.node),KeyOfValue()(v))){//小于新值（表示遇到小的數值，將插在右側）return std::pair<iterator,bool>(__insert(x,y,v), true);}}//至此 表示新值一定和樹中的鍵值重復 就不應該插入新的數值return std::pair<iterator,bool>(j, false);
}//真正的插入執行程序 __insert()
template <class Key,class Value,class KeyOfValue,class Compare,class Alloc>
typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iterator
rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::__insert(base_ptr x_, base_ptr y_, const value_type &v) {//參數x_為新的插入點 參數y_為插入點的父節點 參數v為新值link_type x = (link_type)x_;link_type y = (link_type)y_;link_type z ;//key_compare 是鍵值大小的比較準則，應該是一個function objectif (y == header||x != 0||key_compare(KeyOfValue()(v),key(x))){z = create_node(v); //產生一個新的節點//當y即為header的時候，leftmost = z;if (y == header){root() = z;right_most() = z;} else if (y == left_most()){//y為最左節點//維護leftmost() 使其永遠指向最左節點left_most() = z;} else{z = create_node(v);//產生一個新的節點//讓新節成為插入點的父節點y的右子節點right(y) = z;if (y == right_most()){ //維護rightmost()讓其永遠指向最右的節點right_most() = z;}}parent(z) = y; //設定新節點的父節點left(z) = 0; //設定新節點的左子節點right(z) = 0; //設定新節點的右子節點//修改顏色//參數一為新增節點 ；參數二 為root__rb_tree_rebalance(z,header->parent);++node_count;//返回一個迭代器 指向新的節點return iterator(z);}
}//全局函數
//新節點必須為紅色，如果插入出父節點同樣為紅色，就需要進行樹形旋轉
inline void __rb_tree_rotate_left(__rb_tree_node_base* x,__rb_tree_node_base*& root){//x為旋轉點__rb_tree_node_base* y = x->right;//令y為旋轉點的右子節點x->right = y->left;if (y->left != 0){//回馬槍設定父親節點y->left->parent = x;}y->parent = x->parent;//令y完全替代x的地位 (需要將x對其父節點的關系完全接收回來)if (x == root){root = y; //x為根節點} else if (x == x->parent->left){x->parent->left = y;  //x為其父節點的左子節點} else{x->parent->right = y; //x為其父節點的右子節點}y->left = x;x->parent = y;
}//全局函數
//新節點必須為紅色，如果插入出父節點同樣為紅色，就需要進行樹形旋轉
inline void __rb_tree_rotate_right(__rb_tree_node_base* x,__rb_tree_node_base*& root){//x為旋轉點__rb_tree_node_base* y = x->left; //y為旋轉點的左子節點x->left = y->right;if (y->right != 0){y->right->parent = x;}y->parent = x->parent;//令y完全替代x的地位if(x == root){root = y;} else if (x == x->parent->right){x->parent->right = y;} else{x->parent->left = y;}y->parent = x;x->parent = y;
}//調整RB_tree 插入節點之后，需要進行調整(顏色/翻轉)從而滿足要求
inline void __rb_tree_balance(__rb_tree_node_base* x,__rb_tree_node_base*& root){x->color = __rb_tree_red; //新節點的顏色必須是紅色的while(x!=root && x->parent->color == __rb_tree_red){//父節點為紅色的//父節點為祖父節點的左子節點if (x->parent == x->parent->parent->left){//令y為伯父節點__rb_tree_node_base* y = x->parent->right;if (y && y->color == __rb_tree_red){ //伯父節點存在 且為紅x->parent->color = __rb_tree_black;//更改父節點的顏色為黑y->color = __rb_tree_black;//更改父節點的顏色為黑x->parent->parent->color = __rb_tree_red;//更改祖父節點的顏色為紅x = x->parent->parent;} else{//無伯父節點 或者伯父節點的顏色為黑if (x == x->parent->right){//新節點為父節點的右子節點x = x->parent;//第一次參數為左旋節點__rb_tree_rotate_left(x,root);}x->parent->color = __rb_tree_black;//改變顏色x->parent->parent->color = __rb_tree_red;//第一次參數為右旋節點__rb_tree_rotate_right(x->parent->parent,root);}} else{//父節點為祖父節點的右子節點__rb_tree_node_base* y = x->parent->parent->left; //令y為伯父節點if (y && y->color == __rb_tree_red){ //存在伯父節點，且為紅x->parent->color = __rb_tree_black;//更改父節點為黑y->color = __rb_tree_black;//更改伯父節點為黑x->parent->parent->color = __rb_tree_red; //更改祖父節點為紅x = x->parent->parent; //準備繼續往上層檢查} else{//無伯父節點 或者伯父節點 為黑if (x == x->parent->left){//新節點 為 父節點的左子節點x = x->parent;__rb_tree_rotate_right(x,root); //第一參數為右旋轉點}x->parent->color = __rb_tree_black;//改變顏色x->parent->parent->color = __rb_tree_red;//第一參數為左旋點__rb_tree_rotate_left(x->parent->parent,root);}}} //while結束root->color = __rb_tree_black;
}//元素查找程序
template <class Key,class Value,class KeyOfValue,class Compare,class Alloc>
typename rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::iterator
rb_tree<Key,Value,KeyOfValue,Compare,Alloc>::find(const value_type &k) {link_type y = header; //last node which is  not less than klink_type x = root(); //current nodewhile(x != 0){//key_compare 是節點大小的比較準則 function objectif (!key_compare(key(x),k)){//進行到這里 表示x的數值大于k 。遇到大的數值向左走y = x,x = left(x);} else{x = right(x);}}iterator j = iterator (y);return (j == end() || key_compare(k,key(j.node))) ? end() : j;
}

參考鏈接

• STL源碼：紅黑樹_Sunshine的專欄-CSDN博客