本文給出二叉搜索樹介紹和實現

?

首先說它的性質：所有的節點都滿足，左子樹上所有的節點都比自己小，右邊的都比自己大。

?

那這個結構有什么有用呢？

首先可以快速二分查找。還可以中序遍歷得到升序序列，等等。。。

基本操作：

1、插入某個數值

2、查詢是否包含某個數值

3、刪除某個數值

?

根據實現不同，還可以實現其他很多種操作。

?

實現思路思路：

前兩個操作很好想，就是不斷比較，大了往左走，小了往右走。到空了插入，或者到空都沒找到。

而刪除稍微復雜一些，有下面這幾種情況：

1、需要刪除的節點沒有左兒子，那就把右兒子提上去就好了。

2、需要刪除的節點有左兒子，這個左兒子沒有右兒子，那么就把左兒子提上去

3、以上都不滿足，就把左兒子子孫中最大節點提上來。

?

當然，反過來也是成立的，比如右兒子子孫中最小的節點。

?

下面來敘述為什么可以這么做。

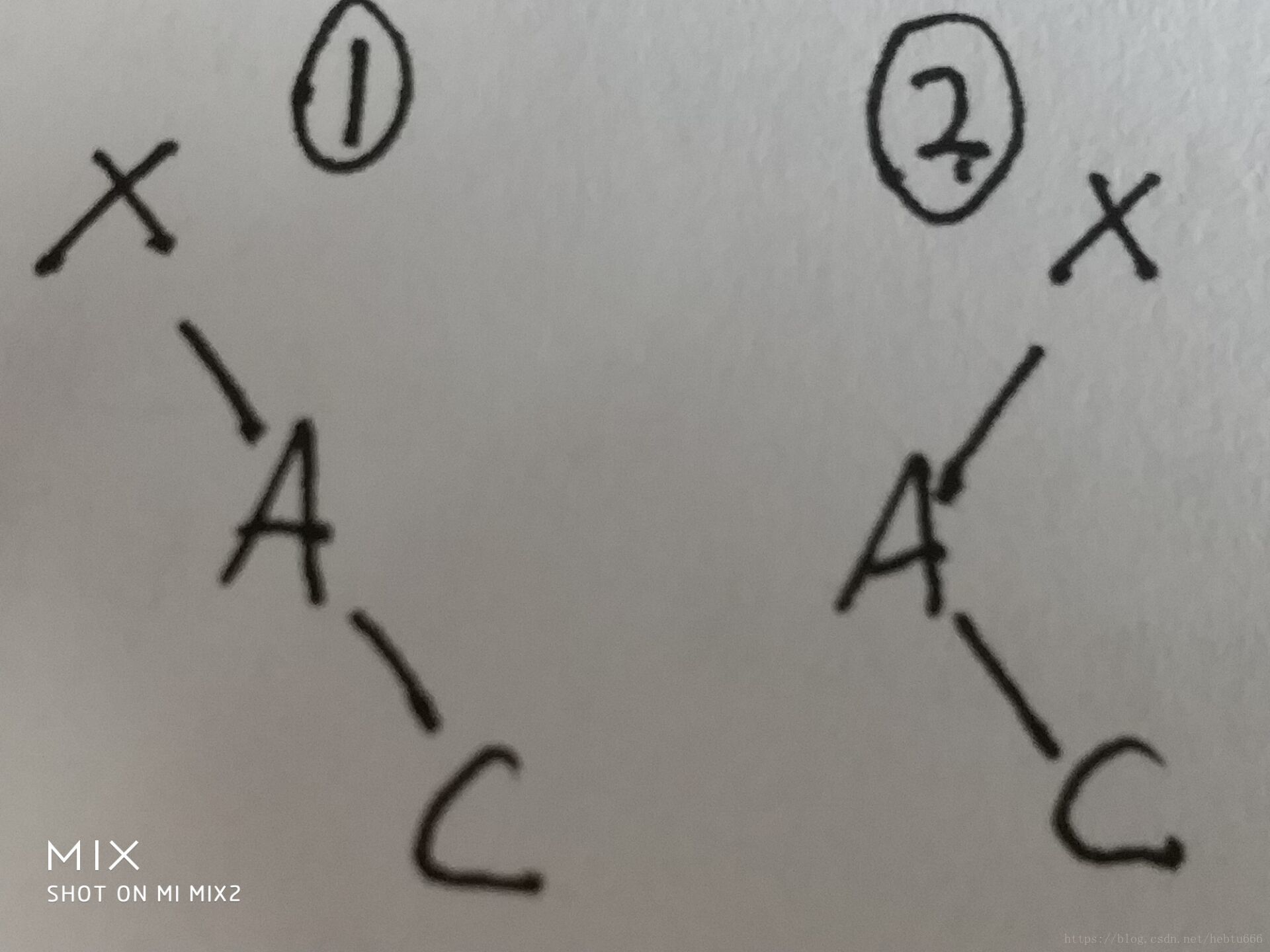
下圖中A為待刪除節點。

第一種情況：

?

1、去掉A，把c提上來，c也是小于x的沒問題。

2、根據定義可知，x左邊的所有點都小于它，把c提上來不影響規則。

?

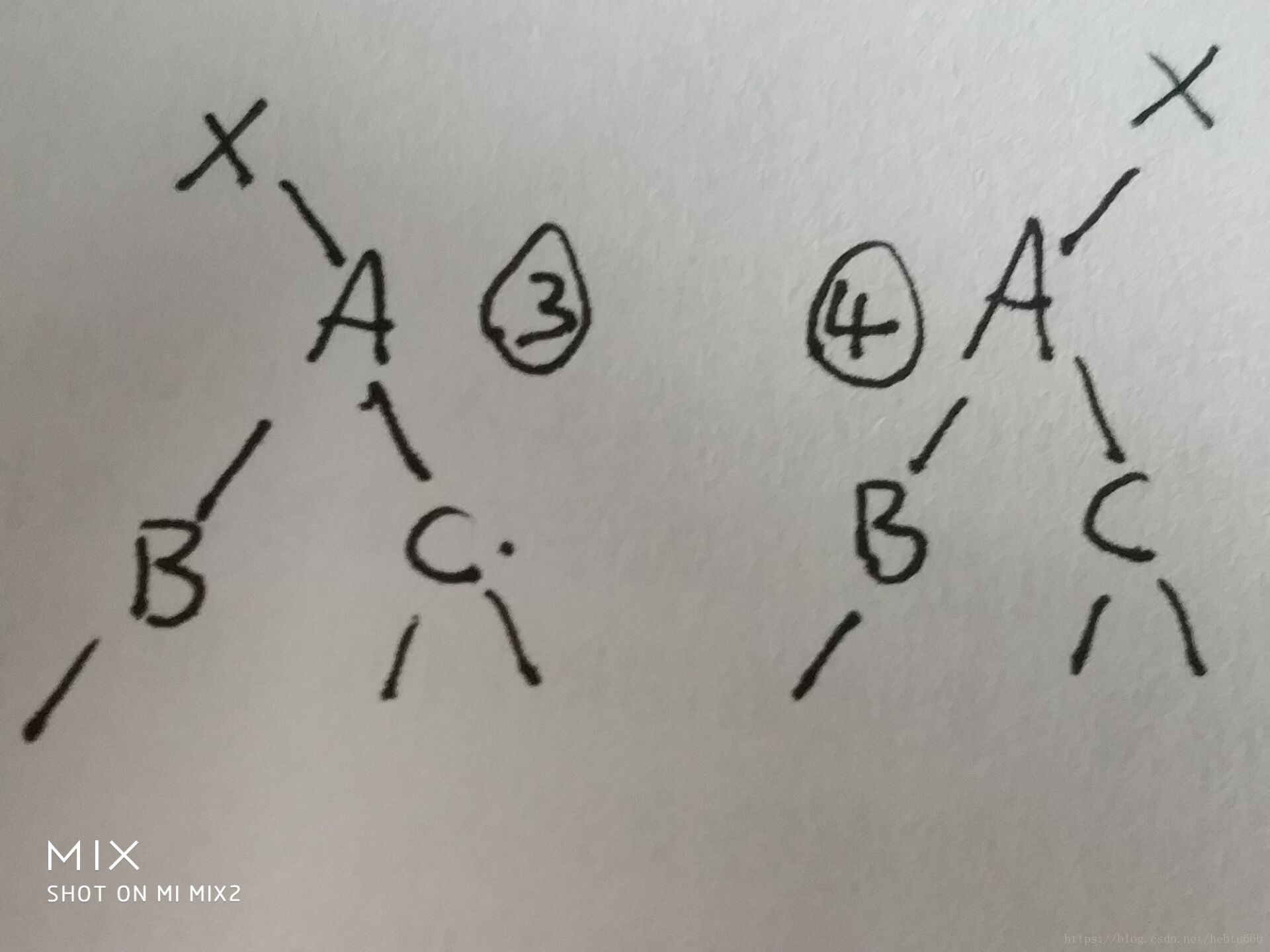
第二種情況

?

3、B<A<C,所以B<C,根據剛才的敘述，B可以提上去，c可以放在b右邊，不影響規則

4、同理

?

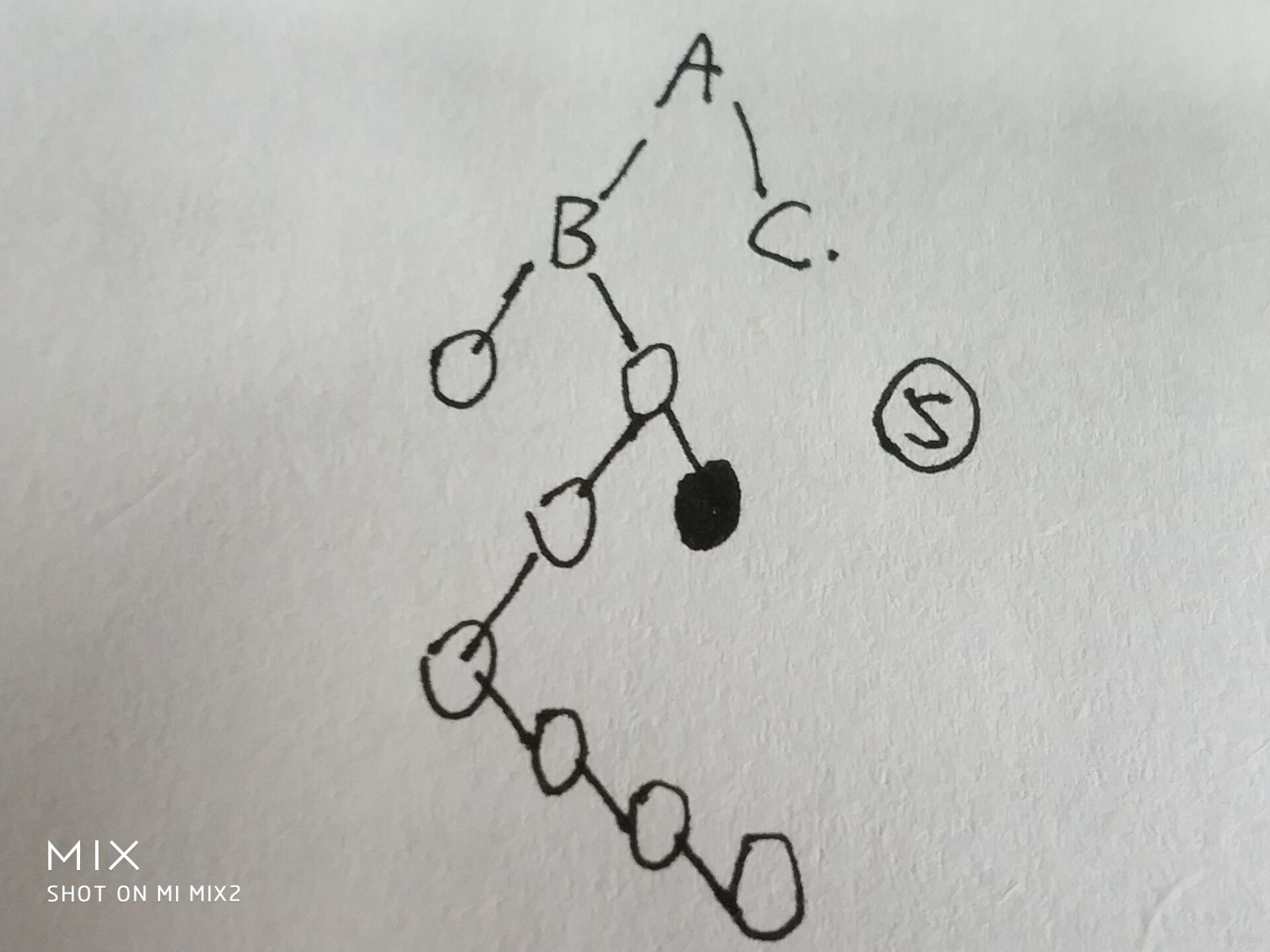
第三種情況

?

5、注意：是把黑色的提升上來，不是所謂的最右邊的那個，因為當初向左拐了，他一定小。

因為黑色是最大，比B以及B所有的孩子都大，所以讓B當左孩子沒問題

而黑點小于A，也就小于c，所以可以讓c當右孩子

大概證明就這樣。。

下面我們用代碼實現并通過注釋理解

上次鏈表之類的用的c，循環來寫的。這次就c++函數遞歸吧，不同方式練習。

定義

struct node
{int val;//數據node *lch,*rch;//左右孩子
};

插入

 node *insert(node *p,int x){if(p==NULL)//直到空就創建節點{node *q=new node;q->val=x;q->lch=q->rch=NULL;return p;}if(x<p->val)p->lch=insert(p->lch,x);else p->lch=insert(p->rch,x);return p;//依次返回自己，讓上一個函數執行。}

查找

 bool find(node *p,int x){if(p==NULL)return false;else if(x==p->val)return true;else if(x<p->val)return find(p->lch,x);else return find(p->rch,x);}

刪除

 node *remove(node *p,int x){if(p==NULL)return NULL;else if(x<p->val)p->lch=remove(p->lch,x);else if(x>p->val)p->lch=remove(p->rch,x);//以下為找到了之后else if(p->lch==NULL)//情況1{node *q=p->rch;delete p;return q;}else if(p->lch->rch)//情況2{node *q=p->lch;q->rch=p->rch;delete p;return q;}else{node *q;for(q=p->lch;q->rch->rch!=NULL;q=q->rch);//找到最大節點的前一個node *r=q->rch;//最大節點q->rch=r->lch;//最大節點左孩子提到最大節點位置r->lch=p->lch;//調整黑點左孩子為Br->rch=p->rch;//調整黑點右孩子為cdelete p;//刪除return r;//返回給父}return p;}

?