找個時間寫一寫時間復雜度和一些問題分類，也普及一下這方面知識。

如何衡量一個算法好壞

很顯然，最重要的兩個指標：需要多久可以解決問題、解決問題耗費了多少資源

那我們首先說第一個問題，要多長時間來解決某個問題。那我們可以在電腦上真實的測試一下嘛，多種方法比一比，用時最少的就是最優的啦。

但是沒必要，我們可以通過分析計算來確定一個方法的好壞，用O()表示，括號內填入N、1，等式子。

這到底是什么意思呢？

簡單來說，就是這個方法，時間隨著數據規模變化而增加的快慢。時間可以當成Y，數據規模是X，y=f(x)，就這樣而已。但是f(x)不是準確的，只是一個大致關系，y=10x,我們也視作x，因為他的增長速度還是n級別的。現在就可以理解了：一般O(N)就是對每個對象訪問優先次數而已。請注意：O(1)它不是每個元素訪問一次，而是Y=1的感覺，y不隨x變化而變化，數據多大它的時間是不變的，有限的常數操作即可完成。

那我們就引入正規概念：

時間復雜度是同一問題可用不同算法解決，而一個算法的質量優劣將影響到算法乃至程序的效率。算法分析的目的在于選擇合適算法和改進算法。

計算機科學中，算法的時間復雜度是一個函數，它定性描述了該算法的運行時間。這是一個關于代表算法輸入值的字符串的長度的函數。時間復雜度常用大O符號表述，不包括這個函數的低階項和首項系數。使用這種方式時，時間復雜度可被稱為是漸近的，它考察當輸入值大小趨近無窮時的情況。

注意：文中提到：不包括這個函數的低階項和首項系數。什么意思呢？就是說10n,100n,哪怕1000000000n,還是算做O(N)，而低階項是什么意思？不知大家有沒有學高等數學1，里面有最高階無窮大，就是這個意思。舉個例子。比如y=n*n*n+n*n+n+1000

就算做o(n*n*n),因為增長速率最大，N*N及其它項增長速率慢，是低階無窮大，n無限大時，忽略不計。

?

那接著寫：o(n*n*n)的算法一定不如o(n)的算法嗎？也不一定，因為之前說了，時間復雜度忽略了系數，什么意思？o(n)可以是10000000n，當n很小的時候，前者明顯占優。

所以算法要視實際情況而定。

算法的時間 復雜度常見的有：
常數階 O(1)，對數階 O(log n)，線性階 O(n)，
線性對數階 O(nlog n)，平方階 O(n^2)，立方階 O(n^3)，…，
k 次方階O(n^k)，指數階 O(2^n)，階乘階 O(n!)。

常見的算法的時間 復雜度之間的關系為：
?????? O(1)<O(log n)<O(n)<O(nlog n)<O(n^2)<O(2^n)<O(n!)<O(n^n)?

?

我們在競賽當中，看見一道題，第一件事就應該是根據數據量估計時間復雜度。

計算機計算速度可以視作10^9,如果數據量是10000，你的算法是O(N*N)，那就很玄，10000*10000=10000 0000，別忘了還有常數項，這種算法只有操作比較簡單才可能通過。你可以想一想O(nlog n)的算法一般就比較穩了。那數據量1000，一般O(N*N)就差不多了，數據量更小就可以用復雜度更高的算法。大概就這樣估算。

?

當 n 很大時，指數階算法和多項式階算法在所需時間上非常
懸殊。因此，只要有人能將現有指數階算法中的任何一個算法化
簡為多項式階算法，那就取得了一個偉大的成就。

體會一下：

?

空間復雜度也是一樣，用來描述占空間的多少。

注意時間空間都不能炸。

所以才發明了那么多算法。

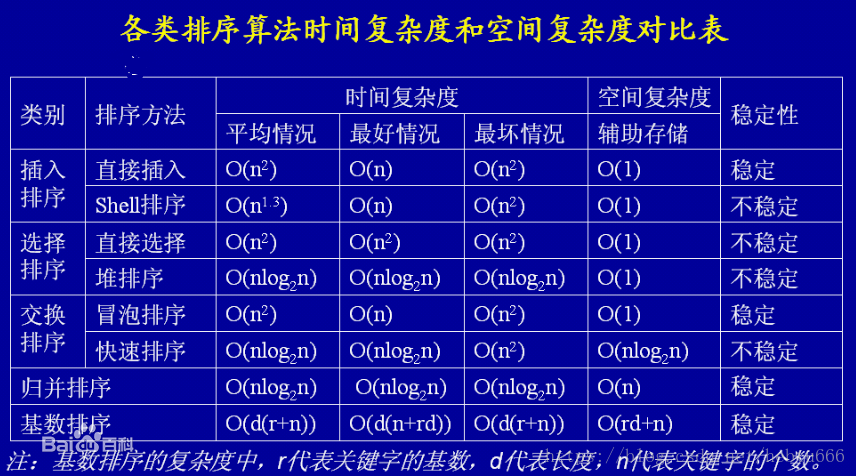
符上排序算法的時間空間表，體會一下：

?

排序博客：加深對時間空間復雜度理解

https://blog.csdn.net/hebtu666/article/details/81434236

?

?

相關擴展：https://blog.csdn.net/hebtu666/article/details/82465495

?

?

?