關系

1. 域：一組具有相同數據類型的值的集合（即取值范圍）

2. 笛卡爾積：域上的一種集合運算。結果為一個集合，集合的每一個元素是一個元組，元組的每一個分量來自不同的域。

3. 基數：一個域允許的不同取值個數。

4. 笛卡爾積的基數：每個域不同取值的個數的乘積，或者說元組的個數

5. 關系：域的笛卡爾積的子集叫做在域上的關系，域的個數叫做關系的目或度。（即列數，屬性的數目），注意廣義上的笛卡爾積一般不能稱為關系，因為存在無效的數據。

6. 關系：表

   列：屬性

   行：元組

7. 候選碼：某一屬性組的值能唯一地標示一個元組，而其子集不能，則稱該屬性組為候選碼

8. 主屬性：候選碼中的屬性都稱為主屬性，注意：主屬性非空。

9. 非主屬性：候選碼之外的屬性稱為非主屬性

10. 全碼：關系模式的所有屬性是這個關系模式的候選碼

11. 主碼：從候選碼中選取一組能唯一確定一個元組的屬性組作為主碼。

12. 三類關系：

    1）基本關系：實際存在的表，是實際存儲數據的邏輯表示

    2）查詢表：查詢結果對應的表

    3）視圖表：由基本表或其他視圖表導出的表，是虛表，不對應實際存儲的數據。

    注意：關系數據模型中的關系必須是有限集合。

    關系的每一個列必須附加一個屬性名，屬性名不能重名，這種方法取消了關系屬性的有序性。

13. ① 列是同質的（Homogeneous）：每一列中的分量來自同一個域，是同一類型的數據

    ② 不同的列可出自同一個域

    • 其中的每一列稱為一個屬性

    • 不同的屬性要給予不同的屬性名

    ③ 列的順序無所謂, 列的次序可以任意交換

    ④ 任意兩個元組的候選碼不能相同：相同就不是候選碼了

    ⑤ 行的順序無所謂，行的次序可以任意交換

    ⑥ 分量必須取原子值（不允許表中套表）

關系模式

?

1. 關系模式：對關系的描述，是靜態的、穩定的

2. 關系：是關系模式在某一時刻的狀態或內容，是動態的、隨時間不斷變化的，指后邊的那個關系

3. 關系模式的形式化表示：

//關系模式
R(U, D, DOM, F)
R       關系名
U       組成該關系的屬性名集合
D       屬性組U中屬性所來自的域
DOM  	屬性向域的映象集合
F       屬性間的數據依賴關系集合//可以簡記為
R (U)    或    R (A1，A2，…，An)
R: 關系名
A1，A2，…，An  : 屬性名
注：域名及屬性向域的映象常常直接說明為屬性的類型、長度

關系數據庫

1. 在一個給定的應用領域中，所有關系的集合構成一個關系數據庫

2. 關系數據庫的型與值，不是關系的型與值

   1）關系數據庫的型也稱關系數據庫模式，是對關系數據庫的描述

   2）關系數據庫的值是關系模式在某一時刻對應的關系的集合，簡稱為關系數據庫

基本的關系操作

1. 常用的基本操作：

   **查詢：**選擇、投影、連接、除、并、交、差

   **數據更新：**插入、刪除、修改

2. **5種基本操作：**選擇、投影、并、差、笛卡爾積?注意：不算交

3. 關系操作的特點：

   集合操作方式：操作的對象和結果都是集合，一次一集合的方式，操作對象是集合，操作結果亦為集合。

?

關系的完整性

實體完整性（即主屬性非空）

1. 若屬性A是基本關系R的主屬性，則屬性A不能取空值

參照完整性

1. 關系間的引用：關系與關系之間存在著聯系

2. 外碼：設F是基本關系R的一個或一組屬性，但不是關系R的主碼，Ks是基本關系S的主碼。如果F與Ks相對應，則稱F是基本關系R的外碼，外碼所在的基本關系叫做參照關系，Ks所在的關系叫做被參照關系。

   注：

   1）R、S不一定是不同的關系。

   2）目標關系S的主碼Ks 和參照關系的外碼F必須定義在同一個（或一組）域上

   3）外碼并不一定要與相應的主碼同名，當外碼與相應的主碼屬于不同關系時，往往取相同的名字，以便于識別

   4）外碼的取值：如果外碼是參照關系的主屬性，則不能為空（實體完整性），只能為被參照關系中主碼的取值。如果外碼不是參照關系的主屬性，則可以取空或者被參照關系主碼的取值

3. 兩個不變性：指實體完整性和參照完整性

用戶定義完整性

1. 針對某一具體關系數據庫的約束條件，反映某一具體應用所涉及的數據必須滿足的語義要求

2. 關系模型應提供定義和檢驗這類完整性的機制，以便用統一的系統的方法處理它們，而不要由應用程序承擔這一功能

關系代數

傳統的集合運算

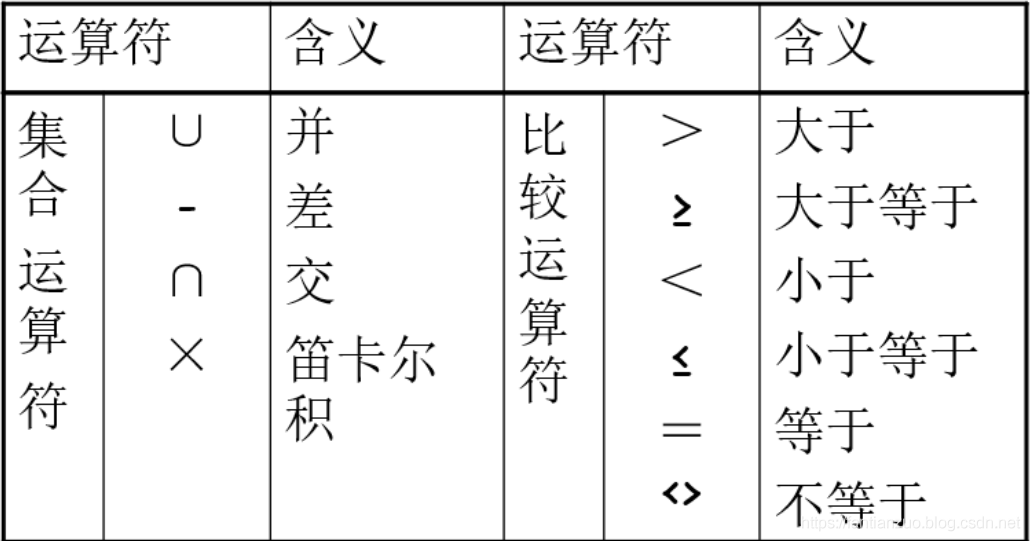
1. 傳統的關系運算：

   并、交、差、笛卡爾積

1. 操作對象關系：

   操作方式：同數學中的并、交、差、笛卡爾積。只不過操作對象的元素是元組。另外需要注意能進行運算所需要滿足的條件。

   對于并、交、差需要滿足的關系：1）屬性的數目相同；2）相應的屬性取自同一個域

專門的關系運算

常見的關系運算有選擇、投影、連接、除

選擇：

在關系R中選擇滿足給定條件的諸元組。

表達式：$\sigma_F(R) = {t | t \in R \and F(t) = ''true''}$

F：為選擇條件，是一個邏輯表達式，基本形式為：$X_1 \theta Y_1$，其中$\theta$為大于、小于、等于、不等于等。

舉例：

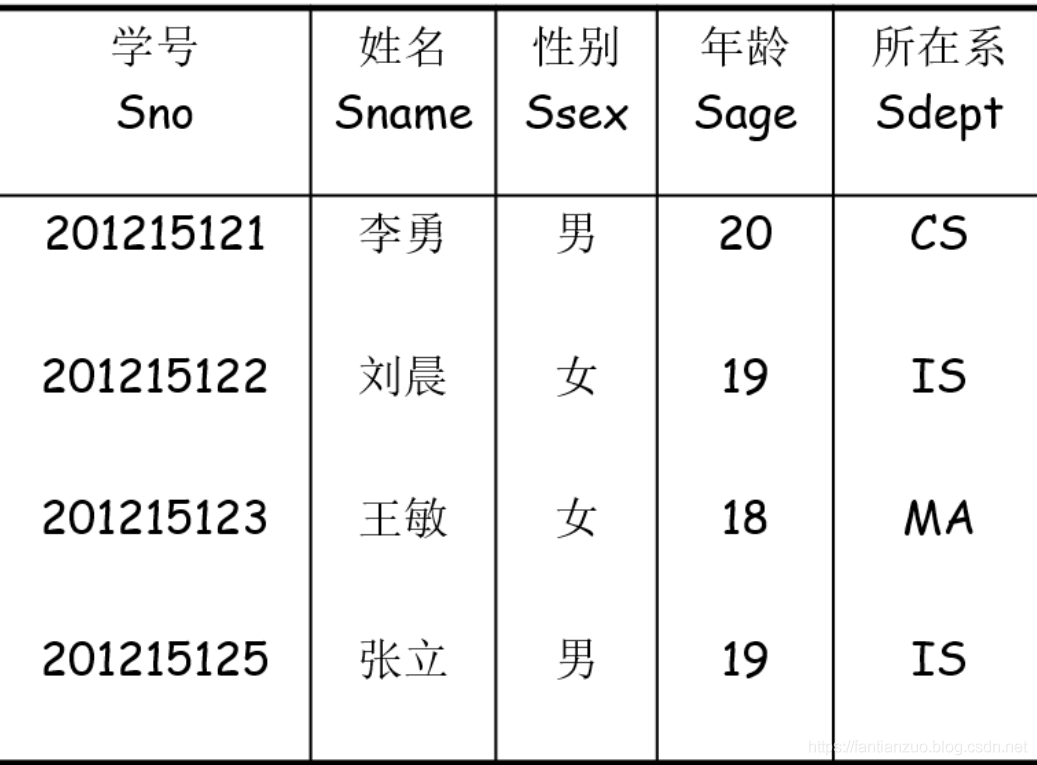
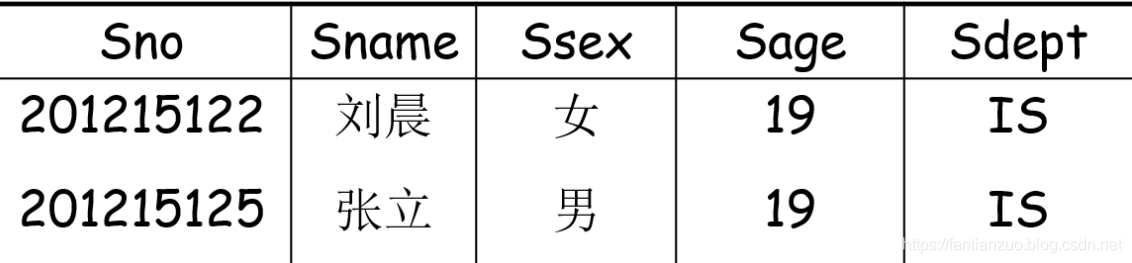
選擇：$\sigma_{Sdept = "IS"}(Student)$

???????

投影：

從R中選擇出若干屬性列組成新的關系

表達式：$\prod_{A} (R)= {t[A] | t\in R}$

A為屬性列，即從R中選擇A中屬性列的元組，當然選擇之后可能會刪掉一些元組，因為避免重復。

舉例：還是上方的關系，經過投影$\prod_{Sname, Sdept}(Student)$，結果如下：

?

連接

?

1）**一般連接：**從兩個關系的笛卡爾積中選取屬性間滿足一定條件的元組

（1）表達式：$R\bowtie_ {A \theta B} S = {t_r^ \frown t_s | t_r \in R \and t_s \in S \and t_r[A] \theta t_s[B] }$

（2）A和B：分別為R和S上度數相等且可比的屬性組

（3）$\theta$表示比較運算符，

（4）連接運算從R和S的廣義笛卡爾積R×S中選取（R關系）在A屬性組上的值與（S關系）在B屬性組上值滿足比較關系θ的元組

2）**等值連接：**當上述的運算符為等于號的時候

（1）含義：從關系R與S的廣義笛卡爾積中選取A、B屬性值相等的那些元組，即等值連接為：

（2）表達式：$R\bowtie_ {A = B} S = {t_r^ \frown t_s | t_r \in R \and t_s \in S \and t_r[A] = t_s[B] }$

（3）仍然是從行的角度進行運算，而不涉及列

（4）屬性組可以不同

3）**自然連接：**一種特殊的等值連接

（1）與等值連接的不同：兩個關系R和S必須具有相同的屬性組

（2）將結果中相同的屬性列去掉

（3）表達式：$R\bowtie S = {t_r^ \frown t_s | t_r \in R \and t_s \in S \and t_r[A] = t_s[B] }$

4）由自然連接所引發的一系列問題：

（1）懸浮元組：在做自然連接的時候被舍棄的元組

（2）外連接：如果把舍棄的元組也保存在結果關系中，而在其他屬性上填空值(Null)，這種連接就叫做外連接，外連接 = 左外連接 + 右外連接

（3）左外連接：如果只把左邊關系R中要舍棄的元組保留就叫做左外連接

（4）右外連接：如果只把右邊關系S中要舍棄的元組保留就叫做右外連接

除

1）除運算的意義：

（1）假設關系R，S，RS，R關系擁有的屬性是姓名，S關系擁有的屬性是課程，RS關系擁有的屬性是姓名和課程的聯系，則RS/S表示選出所有至少選了表S中所列課程的學生的元組。

（2）如下圖：

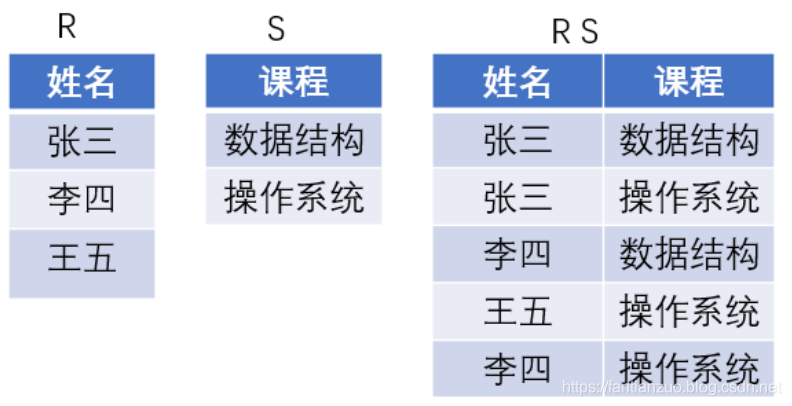
注：RS/S得到的關系：張三和李四構成的表，表示選修了全部課程的同學的集合。

舉例：

R：

A	B	C
a1	b1	c2
a2	b3	c7
a3	b4	c6
a1	b2	c3
a4	b6	c6
a2	b2	c3
a1	b2	c1

S:

B	C	D
b1	c2	d1
b2	c1	d1
b2	c3	d2

R÷S

A
a1

(1) 找S與R的共同屬性，即公式中的Y屬性

(2)計算R中每個X屬性的象集，如果某個象集包含S在Y屬性上的投影，則該屬為R/S結果中的一個值。

解答如下：

在關系R中，A可以取四個值{a1,a2,a3,a4}，其中：

a1的象集為：{（b1,c2），（b2,c3），（b2,c1）}

a2的象集為：{（b3,c7），（b2,c3）}

a3的象集為：{（b4,c6）}

a4的象集為：{（b6,c6）}

S在（B,C）上的投影為{(b1,c2),(b2,c3),(b2,c1)}。

顯然只有R的象集a1包含S在（B,C）屬性組上的投影，所以R÷S={a1}。