文章目錄
- 1.struct和class區別,你更傾向用哪個
- 2.kNN,樸素貝葉斯,SVM的優缺點,各種算法優缺點
- 2.1 KNN算法
- 2.2 樸素貝葉斯
- 2.3SVM算法
- 2.4 ANN算法
- 2.5 DT算法
- 3. 10億個整數,1G內存,O(n)算法,統計只出現一次的數。
- 4、海量數據排序
- 4.1 數據庫排序
- 4.2 分段排序
- 4.3 **bit位操作 **
- 5、項目中的數據是否會歸一化處理,哪個機器學習算法不需要歸一化處理
- 6、RBF核與高斯核的區別
- 7、L1和L2的區別
- 7.1 L1正則化
- 7.2 L2正則化
- 8、有哪些聚類方法?
- 8.1 常用聚類算法:
- 8.2 K-means聚類
- 8.3 層次聚類
- 9、什么是模糊聚類,還有劃分聚類,層次聚類等
- 10、哪些模型容易過擬合,模型怎么選擇
- 10.1 出現過擬合
- 10.2 模型選擇方法
- 11、CART、GBDT
- 11.1 KNN(分類與回歸)
- 11.2 CART
- 11.3 Logistics(推導)
- 11.4 GBDT
- 11.5 RF
- 12、寫SVM的優化形式,用拉格朗日公式推導SVM kernel變換
- 13、數據結構當中的樹,都有哪些
- 14、二分查找算法,遞歸、非遞歸實現,分析時間復雜度
- 15、幾個排序算法,必須寫出(快排)
- 15.1 快速排序
1.struct和class區別,你更傾向用哪個
結構與類共享幾乎所有相同的語法,但結構比類受到的限制更多:
1、盡管結構的靜態字段可以初始化,結構實例字段聲明還是不能使用初始值設定項。
2、結構不能聲明默認構造函數(沒有參數的構造函數)或析構函數。
3、結構的副本由編譯器自動創建和銷毀,因此不需要使用默認構造函數和析構函數。實際上,編譯器通過為所有字段賦予默認值(參見默認值表)來實現默認構造函數。結構不能從類或其他結構繼承。
4、結構是值類型——如果從結構創建一個對象并將該對象賦給某個變量,變量則包含結構的全部值。
結構具有以下特點:
- 結構是值類型,而類是引用類型。
- 向方法傳遞結構時,結構是通過傳值方式傳遞的,而不是作為引用傳遞的。
- 與類不同,結構的實例化可以不使用 new 運算符。
- 結構可以聲明構造函數,但它們必須帶參數。
- 一個結構不能從另一個結構或類繼承,而且不能作為一個類的基。
- 所有結構都直接繼承自 System.ValueType,后者繼承自 System.Object。
- 結構可以實現接口。
- 在結構中初始化實例字段是錯誤的
2.kNN,樸素貝葉斯,SVM的優缺點,各種算法優缺點
2.1 KNN算法
KNN算法非常簡單而且非常有效。 KNN的模型用整個訓練數據集表示。 是不是特簡單?
通過搜索整個訓練集內K個最相似的實例(鄰居),并對這些K個實例的輸出變量進行匯總,來預測新的數據點。 對于回歸問題,新的點可能是平均輸出變量,對于分類問題,新的點可能是眾數類別值。
成功的訣竅在于如何確定數據實例之間的相似性。如果你的屬性都是相同的比例,最簡單的方法就是使用歐幾里德距離,它可以根據每個輸入變量之間的差直接計算。
優點:
- 簡單、有效。
- 重新訓練的代價較低
- 計算時間和空間 線性于 訓練集的規模
- 由于KNN方法主要靠周圍有限的鄰近的樣本,而不是靠判別類域的方法來確定所屬類別的,因此對于類域的交叉或重疊較多的待分樣本集來說,KNN方法較其他方法更為適合。
- 該算法比較適用于樣本容量比較大的類域的自動分類,而那些樣本容量較小的類域采用這種算法比較容易產生誤分。
缺點:
- KNN算法是懶散學習方法(lazy learning,基本上不學習),一些積極學習的算法要快很多。
- 類別評分不是規格化的(不像概率評分)。
- 輸出的可解釋性不強,例如決策樹的可解釋性較強。
- 該算法在分類時有個主要的不足是,當樣本不平衡時,如一個類的樣本容量很大,而其他類樣本容量很小時,有可能導致當輸入一個新樣本時,該樣本的K個鄰居中大容量類的樣本占多數。該算法只計算“最近的”鄰居樣本,某一類的樣本數量很大,那么或者這類樣本并不接近目標樣本,或者這類樣本很靠近目標樣本。無論怎樣,數量并不能影響運行結果。可以采用權值的方法(和該樣本距離小的鄰居權值大)來改進。
- 計算量較大。目前常用的解決方法是事先對已知樣本點進行剪輯,事先去除對分類作用不大的樣本
2.2 樸素貝葉斯
樸素貝葉斯是一種簡單但極為強大的預測建模算法。
該模型由兩種類型的概率組成,可以直接從你的訓練數據中計算出來:1)每個類別的概率; 2)給定的每個x值的類別的條件概率。 一旦計算出來,概率模型就可以用于使用貝葉斯定理對新數據進行預測。 當你的數據是數值時,通常假設高斯分布(鐘形曲線),以便可以輕松估計這些概率。
樸素貝葉斯被稱為樸素的原因,在于它假設每個輸入變量是獨立的。 這是一個強硬的假設,對于真實數據來說是不切實際的,但該技術對于大范圍內的復雜問題仍非常有效。
優點:
- 樸素貝葉斯模型發源于古典數學理論,有著堅實的數學基礎,以及穩定的分類效率。
- NBC模型所需估計的參數很少,對缺失數據不太敏感,算法也比較簡單
缺點:
- 理論上,NBC模型與其他分類方法相比具有最小的誤差率。但是實際上并非總是如此,這是因為NBC模型假設屬性之間相互獨立,這個假設在實際應用中往往是不成立的(可以考慮用聚類算法先將相關性較大的屬性聚類),這給NBC模型的正確分類帶來了一定影響。在屬性個數比較多或者屬性之間相關性較大時,NBC模型的分類效率比不上決策樹模型。而在屬性相關性較小時,NBC模型的性能最為良好。
- 需要知道先驗概率。
- 分類決策存在錯誤率
2.3SVM算法
支持向量機也許是最受歡迎和討論的機器學習算法之一。
超平面是分割輸入變量空間的線。 在SVM中,會選出一個超平面以將輸入變量空間中的點按其類別(0類或1類)進行分離。在二維空間中可以將其視為一條線,所有的輸入點都可以被這條線完全分開。 SVM學習算法就是要找到能讓超平面對類別有最佳分離的系數。
超平面和最近的數據點之間的距離被稱為邊界,有最大邊界的超平面是最佳之選。同時,只有這些離得近的數據點才和超平面的定義和分類器的構造有關,這些點被稱為支持向量,他們支持或定義超平面。在具體實踐中,我們會用到優化算法來找到能最大化邊界的系數值。在小數據集上可以表現比較好
優點:
- 可以解決小樣本情況下的機器學習問題。
- 可以提高泛化性能。
- 可以解決高維問題。
- 可以解決非線性問題。
- 可以避免神經網絡結構選擇和局部極小點問題。
缺點: - 對缺失數據敏感。
- 對非線性問題沒有通用解決方案,必須謹慎選擇Kernel function來處理。
2.4 ANN算法
優點:
- 分類的準確度高
- 并行分布處理能力強,分布存儲及學習能力強
- 對噪聲神經有較強的魯棒性和容錯能力
- 能充分逼近復雜的非線性關系,具備聯想記憶的功能等。
缺點: - 神經網絡需要大量的參數,如網絡拓撲結構、權值和閾值的初始值;
- 不能觀察之間的學習過程,輸出結果難以解釋,會影響到結果的可信度和可接受程度;
- 學習時間過長,甚至可能達不到學習的目的
2.5 DT算法
決策樹是機器學習的一種重要算法。
決策樹模型可用二叉樹表示。對,就是來自算法和數據結構的二叉樹,沒什么特別。 每個節點代表單個輸入變量(x)和該變量上的左右孩子(假定變量是數字)
決策樹學習速度快,預測速度快。 對于許多問題也經常預測準確,并且你不需要為數據做任何特殊準備。
優點:
- 決策樹易于理解和解釋.人們在通過解釋后都有能力去理解決策樹所表達的意義。
- 對于決策樹,數據的準備往往是簡單或者是不必要的.其他的技術往往要求先把數據一般化,比如去掉多余的或者空白的屬性。
- 能夠同時處理數據型和常規型屬性。其他的技術往往要求數據屬性的單一。
- 決策樹是一個白盒模型。如果給定一個觀察的模型,那么根據所產生的決策樹很容易推出相應的邏輯表達式。
- 易于通過靜態測試來對模型進行評測。表示有可能測量該模型的可信度。
- 在相對短的時間內能夠對大型數據源做出可行且效果良好的結果。
- 可以對有許多屬性的數據集構造決策樹。
- 決策樹可很好地擴展到大型數據庫中,同時它的大小獨立于數據庫的大小。
缺點:
- 對于那些各類別樣本數量不一致的數據,在決策樹當中,信息增益的結果偏向于那些具有更多數值的特征。
- 決策樹處理缺失數據時的困難。
- 過度擬合問題的出現。
- 忽略數據集中屬性之間的相關性。
3. 10億個整數,1G內存,O(n)算法,統計只出現一次的數。

4、海量數據排序
4.1 數據庫排序
將文本文件導入到數據庫,讓數據庫進行索引排序操作后提取數據到文件
優點:操作簡單
缺點:運算速度慢,而且需要數據庫設備。
4.2 分段排序
操作方式:
規定一個內存大小,比如200M,200M可以記錄(20010241024/4) = 52428800條記錄,我們可以每次提取5000萬條記錄到文件進行排序,要裝滿9位整數需要20次,所以一共要進行20次排序,需要對文件進行20次讀操作
缺點:
編碼復雜,速度也慢(至少20次搜索)
關鍵步驟:
先將整個9位整數進行分段,億條數據進行分成20段,每段5000萬條
在文件中依次搜索05000萬,500000011億……
將排序的結果存入文件
4.3 **bit位操作 **
思考下面的問題:
一個最大的9位整數為999999999
這9億條數據是不重復的
可不可以把這些數據組成一個隊列或數組,讓它有0~999999999(10億個)元素
數組下標表示數值,節點中用0表示這個數沒有,1表示有這個數
判斷0或1只用一個bit存儲就夠了
聲明一個可以包含9位整數的bit數組(10億),一共需要10億/8=120M內存
把內存中的數據全部初始化為0, 讀取文件中的數據,并將數據放入內存。比如讀到一個數據為341245909這個數據,那就先在內存中找到341245909這個bit,并將bit值置為1遍歷整個bit數組,將bit為1的數組下標存入文件
5、項目中的數據是否會歸一化處理,哪個機器學習算法不需要歸一化處理
一般基于梯度下降的算法都需要進行歸一化處理
量綱問題:歸一化有利于優化迭代速度(梯度下降),提高精度(KNN)
SVM需要歸一化
LDA、DT 不需要歸一化
6、RBF核與高斯核的區別

7、L1和L2的區別
7.1 L1正則化
- 計算絕對值之和,用以產生稀疏性,因為它是L0范式的一個最優凸近似,容易優化求解
- L1優點是能夠獲得sparse模型,對于large-scale的問題來說這一點很重要,因為可以減少存儲空間。缺點是加入L1后目標函數在原點不可導,需要做特殊處理。可以做特征篩選
7.2 L2正則化
- 計算平方和再開根號,L2范數更多是防止過擬合,并且讓優化求解變得穩定很快速(這是因為加入了L2范式之后,滿足了強凸)
- L2優點是實現簡單,能夠起到正則化的作用。缺點就是L1的優點:無法獲得sparse模型。實際上L1也是一種妥協的做法,要獲得真正sparse的模型,要用L0正則化。
8、有哪些聚類方法?
8.1 常用聚類算法:
- K-means聚類
- 層次聚類
- SOM聚類(SOM神經網絡)
- FCM聚類
- 譜聚類
- 模糊聚類
8.2 K-means聚類
**優點: **
簡單直接,易于理解,在低維數據集上有不錯的效果。
缺點:
對于高維數據,其計算速度十分慢,主要是慢在計算距離上,它的另外一個缺點就是它需要我們設定希望得到的聚類數k,若我們對于數據沒有很好的理解,那么設置k值就成了一種估計性的工作。
8.3 層次聚類
優點:
1,距離和規則的相似度容易定義,限制少;
2,不需要預先制定聚類數;
3,可以發現類的層次關系(在一些特定領域如生物有很大作用);
缺點:
1,計算復雜度太高(考慮并行化);
2,奇異值也能產生很大影響;
3,算法很可能聚類成鏈狀(一層包含著一層);
9、什么是模糊聚類,還有劃分聚類,層次聚類等
模糊聚類分析一般是指根據研究對象本身的屬性來構造模糊矩陣,并在此基礎上根據一定的隸屬度來確定聚類關系,即用模糊數學的方法把樣本之間的模糊關系定量的確定,從而客觀且準確地進行聚類。
聚類就是將數據集分成多個類或簇,使得各個類之間的數據差別應盡可能大,類內之間的數據差別應盡可能小,即為“最小化類間相似性,最大化類內相似性”原則 。
10、哪些模型容易過擬合,模型怎么選擇
10.1 出現過擬合
- 決策樹
- 神經網絡
- KNN
10.2 模型選擇方法
從訓練集劃分點數據出來形成驗證集來近似測試誤差;
對訓練誤差進行某種轉化來近似測試誤差。
11、CART、GBDT
11.1 KNN(分類與回歸)
- 分類:取K近鄰中所屬類別數最多的那個類別
- 回歸:取K近鄰中所有樣本的平均值最為該樣本的預測值
11.2 CART
- 回歸樹用平方誤差最小化準則
- 分類樹用基尼指數最小化準則
11.3 Logistics(推導)

11.4 GBDT
- 利用損失函數的負梯度在當前模型的值作為回歸問題提升樹算法中的殘差的近似值,擬合一個回歸樹
11.5 RF
- Bagging+CART
12、寫SVM的優化形式,用拉格朗日公式推導SVM kernel變換
- SVM 凸優化問題
- 拉格朗日對偶(min和max交換順序得到對偶問題)
引入拉格朗日因子
最小化問題中,包含著最大化問題,對偶后得到
求導=0,帶入后得到(被稱為KKT條件)
SVM最佳化形式轉化為只與αn有關
其中,滿足最佳化的條件稱之為Karush-Kuhn-Tucker(KKT)
13、數據結構當中的樹,都有哪些
二叉樹、滿二叉樹、完全二叉樹、二叉排序樹、平衡二叉樹
B樹、B+樹、紅黑樹、鍵樹、字典樹、區間樹與線段樹、敗者樹與勝者樹
14、二分查找算法,遞歸、非遞歸實現,分析時間復雜度
#include <iostream> using namespace std; /*
二分查找思想:
1、數組從小到大排序;
2、查找的key每次和中間數比較,如果key小于mid 查找mid左側的數組部分;
如果key大于mid,則查找mid右側的數組部分;如果相等,則直接返回mid。 輸入:排序數組-array,數組大小-aSize,查找值-key
返回:返回數組中的相應位置,否則返回-1
*/ //非遞歸查找
int BinarySearch(int *array, int aSize, int key)
{ if (array == NULL || aSize == 0 ) return -1; int low = 0; int high = aSize - 1; int mid = 0; while ( low <= high ) { mid = (low + high )/2; if ( array[mid] < key) low = mid + 1; else if ( array[mid] > key ) high = mid - 1; else return mid; } return -1;
} //遞歸
int BinarySearchRecursive(int *array, int low, int high, int key)
{ if ( low > high ) return -1; int mid = ( low + high )/2; if ( array[mid] == key ) return mid; else if ( array[mid] < key ) return BinarySearchRecursive(array, mid+1, high, key); else return BinarySearchRecursive(array, low, mid-1, key);
} int main()
{ int array[10]; for (int i=0; i<10; i++) array[i] = i; cout<<"No recursive:"<<endl; cout<<"position:"<<BinarySearch(array, 10, 6)<<endl; cout<<"recursive:"<<endl; cout<<"position:"<<BinarySearchRecursive(array, 0, 9, 6)<<endl; return 0;
} 
15、幾個排序算法,必須寫出(快排)
15.1 快速排序
快速排序使用分治法(Divide and conquer)策略來把一個串行(list)分為兩個子串行(sub-lists)。
算法步驟:
1 從數列中挑出一個元素,稱為 “基準”(pivot)
2 重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的后面(相同的數可以到任一邊)。在這個分區退出之后,該基準就處于數列的中間位置。這個稱為分區(partition)操作。
3 遞歸地(recursive)把小于基準值元素的子數列和大于基準值元素的子數列排序。 遞歸的最底部情形,是數列的大小是0或1,也就是永遠都已經被排序好了。雖然一直遞歸下去,但是這個算法總會退出,因為在每次的迭代(iteration)中,它至少會把一個元素擺到它最后的位置去。
快速排序是基于分治模式處理的,對一個典型子數組A[p…r]排序的分治過程為三個步驟:
1.分解:
A[p…r]被劃分為倆個(可能空)的子數組A[p …q-1]和A[q+1 …r],
使得 A[p …q-1] <= A[q] <= A[q+1 …r]
2.解決:
通過遞歸調用快速排序,對子數組A[p …q-1]和A[q+1 …r]排序。
3.合并。
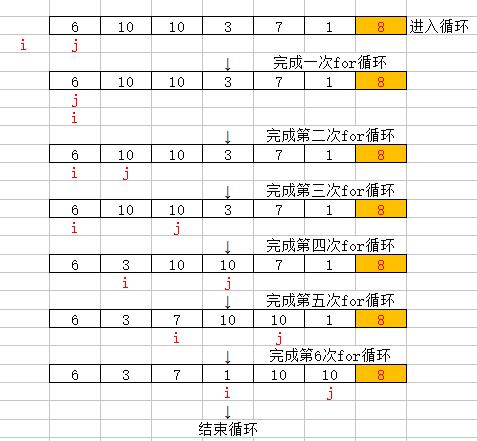
Partition過程:假設數組{6,10,10,3,7,1,8}
(1)從前都和8比較,6小于8,自己和自己交換,不變
(2)10大于8,不進入if
(3)10大于8,不進入if
(4)3小于8,交換到10之前
(5)7小于8,交換到10之前
(6)1小于8,交換到10之前
#include <iostream>
using namespace std;int Partition(int a[], int low, int high)
{int x = a[high]; // 將輸入數組的最后一個數作為主元,用它來對數組進行劃分int i = low - 1; // i是最后一個小于主元的數的下標for (int j = low; j < high; j++) //遍歷下標由low到high-1的數{if (a[j] < x) // 如果數小于主元的話就將i向前挪動一個位置{ // 并且交換j和i所分別指向的數int temp;i++;temp = a[i];a[i] = a[j];a[j] = temp;}}// 經歷上面的循環之后下標為從low到i(包括i)的數就均為小于x的數了// 現在將主元和i+1位置上面的數進行交換a[high] = a[i + 1];a[i + 1] = x;return i + 1;
}
void QuickSort(int a[], int low, int high)
{if (low < high){int q = Partition(a, low, high);QuickSort(a, low, q - 1);QuickSort(a, q + 1, high);}
}int main()
{int buf[10] = { 12, 4, 34, 6, 8, 65, 3, 2, 988, 45 };cout << "排序前:" << endl;for(int i=0;i<10;i++)cout << buf[i] <<" ";QuickSort(buf, 0, 9);cout << "\n\n排序后:" << endl;for(int i=0;i<10;i++)cout << buf[i] <<" ";
}排序前: 12 4 34 6 8 65 3 2 988 45
排序后: 2 3 4 6 8 12 34 45 65 988


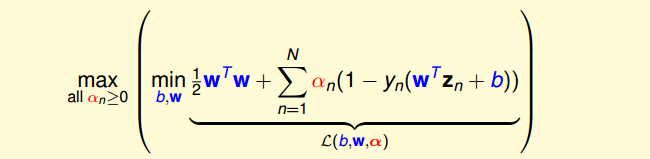
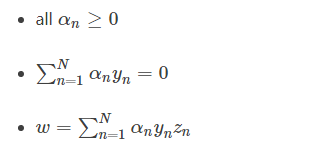
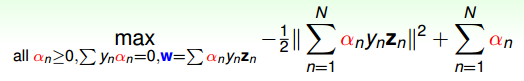


-面向對象2-繼承,多態)

)

-面向對象3-可迭代類對象Pokemon)
)

-單例設計模式)



-異常)

-梯度反向傳播)



-設置隨機種子,復現模型結果)