防止新手錯誤的神級代碼
#define ture true
#define flase false
#difine viod void
#define mian main
#define ; ;
以后有新手問題就把這幾行代碼給他就好啦。
?
不用額外空間交換兩個變量
a?=?5
b?=?8
#計算a和b兩個點到原點的距離之和,并且賦值給a
a?=?a+b
#使用距離之和減去b到原點的距離
#a-b?其實就是a的原值(a到原點的距離),現在賦值給了b
b?=?a-b
#再使用距離之和減去b?(a到原點的距離)
#得到的是b的原值(b到原點的距離),現在賦值給了a
a?=?a-b
八皇后問題神操作
是一個以國際象棋為背景的問題:如何能夠在 8×8 的國際象棋棋盤上放置八個皇后,使得任何一個皇后都無法直接吃掉其他的皇后?為了達到此目的,任兩個皇后都不能處于同一條橫行、縱行或斜線上。八皇后問題可以推廣為更一般的n皇后擺放問題:這時棋盤的大小變為n1×n1,而皇后個數也變成n2。而且僅當 n2 ≥ 1 或 n1 ≥ 4 時問題有解。
皇后問題是非常著名的問題,作為一個棋盤類問題,毫無疑問,用暴力搜索的方法來做是一定可以得到正確答案的,但在有限的運行時間內,我們很難寫出速度可以忍受的搜索,部分棋盤問題的最優解不是搜索,而是動態規劃,某些棋盤問題也很適合作為狀態壓縮思想的解釋例題。
進一步說,皇后問題可以用人工智能相關算法和遺傳算法求解,可以用多線程技術縮短運行時間。本文不做討論。
(本文不展開講狀態壓縮,以后再說)
一般思路:
N*N的二維數組,在每一個位置進行嘗試,在當前位置上判斷是否滿足放置皇后的條件(這一點的行、列、對角線上,沒有皇后)。
優化1:
既然知道多個皇后不能在同一行,我們何必要在同一行的不同位置放多個來嘗試呢?
我們生成一維數組record,record[i]表示第i行的皇后放在了第幾列。對于每一行,確定當前record值即可,因為每行只能且必須放一個皇后,放了一個就無需繼續嘗試。那么對于當前的record[i],查看record[0...i-1]的值,是否有j = record[k](同列)、|record[k] - j| = | k-i |(同一斜線)的情況。由于我們的策略,無需檢查行(每行只放一個)。
public class NQueens {public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}//對于當前行,依次嘗試每列return res;}
//判斷當前位置是否可以放置public static boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}public static void main(String[] args) {int n = 8;System.out.println(num1(n));}
}
位運算優化2:
分析:棋子對后續過程的影響范圍:本行、本列、左右斜線。
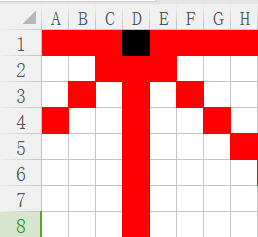
黑色棋子影響區域為紅色
1)本行影響不提,根據優化一已經避免
2)本列影響,一直影響D列,直到第一行在D放棋子的所有情況結束。
3)左斜線:每向下一行,實際上對當前行的影響區域就向左移動
比如:
嘗試第二行時,黑色棋子影響的是我們的第三列;
嘗試第三行時,黑色棋子影響的是我們的第二列;
嘗試第四行時,黑色棋子影響的是我們的第一列;
嘗試第五行及以后幾行,黑色棋子對我們并無影響。
4)右斜線則相反:
隨著行序號增加,影響的列序號也增加,直到影響的列序號大于8就不再影響。
?
我們對于之前棋子影響的區域,可以用二進制數字來表示,比如:
每一位,用01代表是否影響。
比如上圖,對于第一行,就是00010000
嘗試第二行時,數字變為00100000
第三行:01000000
第四行:10000000
?
對于右斜線的數字,同理:
第一行00010000,之后向右移:00001000,00000100,00000010,00000001,直到全0不影響。
?
同理,我們對于多行數據,也同樣可以記錄了
比如在第一行我們放在了第四列:

第二行放在了G列,這時左斜線記錄為00100000(第一個棋子的影響)+00000010(當前棋子的影響)=00100010。
到第三行數字繼續左移:01000100,然后繼續加上我們的選擇,如此反復。
?
這樣,我們對于當前位置的判斷,其實可以通過左斜線變量、右斜線變量、列變量,按位或運算求出(每一位中,三個數有一個是1就不能再放)。
具體看代碼:
注:怎么排版就炸了呢。。。貼一張圖吧
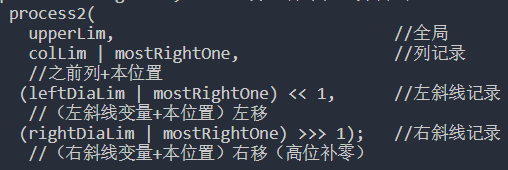
public class NQueens {public static int num2(int n) {// 因為本方法中位運算的載體是int型變量,所以該方法只能算1~32皇后問題// 如果想計算更多的皇后問題,需使用包含更多位的變量if (n < 1 || n > 32) {return 0;}int upperLim = n == 32 ? -1 : (1 << n) - 1;//upperLim的作用為棋盤大小,比如8皇后為00000000 00000000 00000000 11111111//32皇后為11111111 11111111 11111111 11111111return process2(upperLim, 0, 0, 0);}public static int process2(int upperLim, int colLim, int leftDiaLim,int rightDiaLim) {if (colLim == upperLim) {return 1;}int pos = 0; //pos:所有的合法位置int mostRightOne = 0; //所有合法位置的最右位置//所有記錄按位或之后取反,并與全1按位與,得出所有合法位置pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int res = 0;//計數while (pos != 0) {mostRightOne = pos & (~pos + 1);//取最右的合法位置pos = pos - mostRightOne; //去掉本位置并嘗試res += process2(upperLim, //全局colLim | mostRightOne, //列記錄//之前列+本位置(leftDiaLim | mostRightOne) << 1, //左斜線記錄//(左斜線變量+本位置)左移 (rightDiaLim | mostRightOne) >>> 1); //右斜線記錄//(右斜線變量+本位置)右移(高位補零)}return res;}public static void main(String[] args) {int n = 8;System.out.println(num2(n));}
}
完整測試代碼:
32皇后:結果/時間
暴力搜:時間就太長了,懶得測。。。
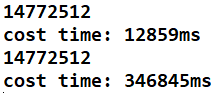
public class NQueens {public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}return res;}public static boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}public static int num2(int n) {if (n < 1 || n > 32) {return 0;}int upperLim = n == 32 ? -1 : (1 << n) - 1;return process2(upperLim, 0, 0, 0);}public static int process2(int upperLim, int colLim, int leftDiaLim,int rightDiaLim) {if (colLim == upperLim) {return 1;}int pos = 0;int mostRightOne = 0;pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int res = 0;while (pos != 0) {mostRightOne = pos & (~pos + 1);pos = pos - mostRightOne;res += process2(upperLim, colLim | mostRightOne,(leftDiaLim | mostRightOne) << 1,(rightDiaLim | mostRightOne) >>> 1);}return res;}public static void main(String[] args) {int n = 32;long start = System.currentTimeMillis();System.out.println(num2(n));long end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + "ms");start = System.currentTimeMillis();System.out.println(num1(n));end = System.currentTimeMillis();System.out.println("cost time: " + (end - start) + "ms");}
}
馬拉車——字符串神級算法
Manacher's Algorithm 馬拉車算法操作及原理?
package advanced_001;public class Code_Manacher {public static char[] manacherString(String str) {char[] charArr = str.toCharArray();char[] res = new char[str.length() * 2 + 1];int index = 0;for (int i = 0; i != res.length; i++) {res[i] = (i & 1) == 0 ? '#' : charArr[index++];}return res;}public static int maxLcpsLength(String str) {if (str == null || str.length() == 0) {return 0;}char[] charArr = manacherString(str);int[] pArr = new int[charArr.length];int C = -1;int R = -1;int max = Integer.MIN_VALUE;for (int i = 0; i != charArr.length; i++) {pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {if (charArr[i + pArr[i]] == charArr[i - pArr[i]])pArr[i]++;else {break;}}if (i + pArr[i] > R) {R = i + pArr[i];C = i;}max = Math.max(max, pArr[i]);}return max - 1;}public static void main(String[] args) {String str1 = "abc1234321ab";System.out.println(maxLcpsLength(str1));}}
問題:查找一個字符串的最長回文子串
首先敘述什么是回文子串:回文:就是對稱的字符串,或者說是正反一樣的
小問題一:請問,子串和子序列一樣么?請思考一下再往下看
?當然,不一樣。子序列可以不連續,子串必須連續。
舉個例子,”123”的子串包括1,2,3,12,23,123(一個字符串本身是自己的最長子串),而它的子序列是任意選出元素組成,他的子序列有1,2,3,12,13,23,123,””,空其實也算,但是本文主要是想敘述回文,沒意義。
小問題二:長度為n的字符串有多少個子串?多少個子序列?
?子序列,每個元素都可以選或者不選,所以有2的n次方個子序列(包括空)
子串:以一位置開頭,有n個子串,以二位置開頭,有n-1個子串,以此類推,我們發現,這是一個等差數列,而等差序列求和,有n*(n+1)/2個子串(不包括空)。
(這里有一個思想需要注意,遇到等差數列求和,基本都是o(n^2)級別的)
一、分析枚舉的效率
好,我們來分析一下暴力枚舉的時間復雜度,上文已經提到過,一個字符串的所有子串,數量是o(n^2)級別,所以光是枚舉出所有情況時間就是o(n^2),每一種情況,你要判斷他是不是回文的話,還需要o(n),情況數和每種情況的時間,應該乘起來,也就是說,枚舉時間要o(n^3),效率太低。
二、初步優化
思路:我們知道,回文全是對稱的,每個回文串都會有自己的對稱軸,而兩邊都對稱。我們如果從對稱軸開始, 向兩邊闊,如果總相等,就是回文,擴到兩邊不相等的時候,以這個對稱軸向兩邊擴的最長回文串就找到了。
舉例:1 2 1 2 1 2 1 1 1
我們用每一個元素作為對稱軸,向兩邊擴
0位置,左邊沒東西,只有自己;
1位置,判斷左邊右邊是否相等,1=1所以接著擴,然后左邊沒了,所以以1位置為對稱軸的最長回文長度就是3;
2位置,左右都是2,相等,繼續,左右都是1,繼續,左邊沒了,所以最長為5
3位置,左右開始擴,1=1,2=2,1=1,左邊沒了,所以長度是7
如此把每個對稱軸擴一遍,最長的就是答案,對么?
你要是點頭了。。。自己扇自己兩下。
還有偶回文呢,,比如1221,123321.這是什么情況呢?這個對稱軸不是一個具體的數,因為人家是偶回文。
問題三:怎么用對稱軸向兩邊擴的方法找到偶回文?(容易操作的)
我們可以在元素間加上一些符號,比如/1/2/1/2/1/2/1/1/1/,這樣我們再以每個元素為對稱軸擴就沒問題了,每個你加進去的符號都是一個可能的偶數回文對稱軸,此題可解。。。因為我們沒有錯過任何一個可能的對稱軸,不管是奇數回文還是偶數回文。
那么請問,加進去的符號,有什么要求么?是不是必須在原字符中沒出現過?請思考
?
其實不需要的,大家想一下,不管怎么擴,原來的永遠和原來的比較,加進去的永遠和加進去的比較。(不舉例子說明了,自己思考一下)
好,分析一波時間效率吧,對稱軸數量為o(n)級別,每個對稱軸向兩邊能擴多少?最多也就o(n)級別,一共長度才n; 所以n*n是o(n^2) ??(最大能擴的位置其實也是兩個等差數列,這么理解也是o(n^2),用到剛講的知識)
?
小結:
這種方法把原來的暴力枚舉o(n^3)變成了o(n^2),大家想一想為什么這樣更快呢?
我在kmp一文中就提到過,我們寫出暴力枚舉方法后應想一想自己做出了哪些重復計算,錯過了哪些信息,然后進行優化。
看我們的暴力方法,如果按一般的順序枚舉,012345,012判斷完,接著判斷0123,我是沒想到可以利用前面信息的方法,因為對稱軸不一樣啊,右邊加了一個元素,左邊沒加。所以剛開始,老是想找一種方法,左右都加一個元素,這樣就可以對上一次的信息加以利用了。
暴力為什么效率低?永遠是因為重復計算,舉個例子:12121211,下標從0開始,判斷1212121是否為回文串的時候,其實21212和121等串也就判斷出來了,但是我們并沒有記下結果,當枚舉到21212或者121時,我們依舊是重新嘗試了一遍。(假設主串長度為n,對稱軸越在中間,長度越小的子串,被重復嘗試的越多。中間那些點甚至重復了n次左右,本來一次搞定的事)
還是這個例子,我換一個角度敘述一下,比較直觀,如果從3號開始向兩邊擴,121,21212,最后擴到1212121,時間復雜度o(n),用枚舉的方法要多少時間?如果主串長度為n,枚舉嘗試的子串長度為,3,5,7....n,等差數列,大家讀到這里應該都知道了,等差數列求和,o(n^2)。
三、Manacher原理
首先告訴大家,這個算法時間可以做到o(n),空間o(n).
好的,開始講解這個神奇的算法。
首先明白兩個概念:
最右回文邊界R:挺好理解,就是目前發現的回文串能延伸到的最右端的位置(一個變量解決)
中心c:第一個取得最右回文邊界的那個中心對稱軸;舉個例子:12121,二號元素可以擴到12121,三號元素 可以擴到121,右邊界一樣,我們的中心是二號元素,因為它第一個到達最右邊界
當然,我們還需要一個數組p來記錄每一個可能的對稱軸最后擴到了哪里。
有了這么幾個東西,我們就可以開始這個神奇的算法了。
為了容易理解,我分了四種情況,依次講解:
?
假設遍歷到位置i,如何操作呢

1)i>R:也就是說,i以及i右邊,我們根本不知道是什么,因為從來沒擴到那里。那沒有任何優化,直接往右暴力 擴唄。
(下面我們做i關于c的對稱點,i’)
2)i<R:,
三種情況:
i’的回文左邊界在c回文左邊界的里面
i’回文左邊界在整體回文的外面
i’左邊界和c左邊界是一個元素
(怕你忘了概念,c是對稱中心,c它當初擴到了R,R是目前擴到的最右的地方,現在咱們想以i為中心,看能擴到哪里。)
按原來o(n^2)的方法,直接向兩邊暴力擴。好的,魔性的優化來了。咱們為了好理解,分情況說。首先,大家應該知道的是,i’其實有人家自己的回文長度,我們用數組p記錄了每個位置的情況,所以我們可以知道以i’為中心的回文串有多長。
2-1)i’的回文左邊界在c回文的里面:看圖
我用這兩個括號括起來的就是這兩個點向兩邊擴到的位置,也就是i和i’的回文串,為什么敢確定i回文只有這么長?和i’一樣?我們看c,其實這個圖整體是一個回文串啊。
串內完全對稱(1是括號左邊相鄰的元素,2是右括號右邊相鄰的元素,34同理),
?由此得出結論1:
由整體回文可知,點2=點3,點1=點4
?
當初i’為什么沒有繼續擴下去?因為點1!=點2。
由此得出結論2:點1!=點2?
?
因為前面兩個結論,所以3!=4,所以i也就到這里就擴不動了。而34中間肯定是回文,因為整體回文,和12中間對稱。
?
2-2)i’回文左邊界在整體回文的外面了:看圖
這時,我們也可以直接確定i能擴到哪里,請聽分析:
當初c的大回文,擴到R為什么就停了?因為點2!=點4----------結論1;
2’為2關于i’的對稱點,當初i’左右為什么能繼續擴呢?說明點2=點2’---------結論2;
由c回文可知2’=3,由結論2可知點2=點2’,所以2=3;
但是由結論一可知,點2!=點4,所以推出3!=4,所以i擴到34為止了,34不等。
而34中間那一部分,因為c回文,和i’在內部的部分一樣,是回文,所以34中間部分是回文。
?
2-3)最后一種當然是i’左邊界和c左邊界是一個元素
點1!=點2,點2=點3,就只能推出這些,只知道34中間肯定是回文,外邊的呢?不知道啊,因為不知道3和4相不相等,所以我們得出結論:點3點4內肯定是,繼續暴力擴。
原理及操作敘述完畢,不知道我講沒講明白。。。
四、代碼及復雜度分析
?看代碼大家是不是覺得不像o(n)?其實確實是的,來分析一波。。
首先,我們的i依次往下遍歷,而R(最右邊界)從來沒有回退過吧?其實當我們的R到了最右邊,就可以結束了。再不濟i自己也能把R一個一個懟到最右
我們看情況一和四,R都是以此判斷就向右一個,移動一次需要o(1)
我們看情況二和三,直接確定了p[i],根本不用擴,直接遍歷下一個元素去了,每個元素o(1).
綜上,由于i依次向右走,而R也沒有回退過,最差也就是i和R都到了最右邊,而讓它們移動一次的代價都是o(1)的,所以總體o(n)
可能大家看代碼依舊有點懵,其實就是code整合了一下,我們對于情況23,雖然知道了它肯定擴不動,但是我們還是給它一個起碼是回文的范圍,反正它擴一下就沒擴動,不影響時間效率的。而情況四也一樣,給它一個起碼是回文,不用驗證的區域,然后接著擴,四和二三的區別就是。二三我們已經心中有B樹,它肯定擴不動了,而四確實需要接著嘗試。
(要是寫四種情況當然也可以。。但是我懶的寫,太多了。便于理解分了四種情況解釋,code整合后就是這樣子)
?
我真的想象不到當初發明這個算法的人是怎么想到的,向他致敬。

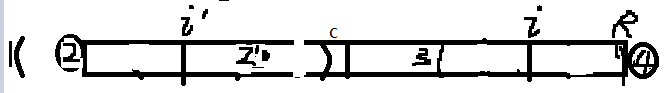

-)

 ubuntu16.04 安裝方法)

-深度推薦模型-AutoRec、DeepCrossing、NeuralCF、PNN、WideDeep、FNN、DeepFM、NFM)
)

)
-)

-注意力機制+深度推薦模型、強化學習推薦系統)


)

 Variable(變量))
-)
 神經網絡)

)