算法概述

當題目出現 「找到最近一個比其大的元素」 的字眼時，自然會想到 「單調棧」 。——三葉姐

單調棧以嚴格遞增or遞減的規則將無序的數列進行選擇性排序。

題目

下一個更大的元素 I

給你兩個 沒有重復元素 的數組 nums1 和 nums2 ，其中 nums1 是 nums2 的子集。（題源力扣）

請你找出 nums1 中每個元素在 nums2 中的下一個比其大的值。

nums1 中數字 x 的下一個更大元素是指 x 在 nums2 中對應位置的右邊的第一個比 x 大的元素。如果不存在，對應位置輸出 -1 。

示例：

輸入： nums1 = [4,1,2], nums2 = [1,3,4,2].
輸出： [-1,3,-1]
解釋：

對于 num1 中的數字 4 ，你無法在第二個數組中找到下一個更大的數字，因此輸出 -1 。
對于 num1 中的數字 1 ，第二個數組中數字 1 右邊的下一個較大數字是 3 。
對于 num1 中的數字 2 ，第二個數組中沒有下一個更大的數字，因此輸出 -1 。

思路

倒序遍歷 nums2 用 stack 暫存嚴格遞增的數據，即，若 棧不為空 且 當前遍歷到的元素大于棧頂元素 則彈出棧頂元素。
用 unordred_map 存儲 遍歷到的元素（key） 和 最近一個比其大的元素（value） 之間的關系。經過步驟一后，若棧不為空，則棧頂元素即為 value ，否則，value 為 -1 。
正序遍歷 nums1 并依賴 unordred_map 得到題目要求的結果數組。

代碼

class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {unordered_map<int, int> m;stack<int> st;for(int i = nums2.size()-1; i >= 0; i--){int t = nums2[i];while(st.size() && t>st.top()) st.pop();m[t] = st.empty() ? -1 : st.top();st.push(t);}vector<int> v;for(int i = 0; i < nums1.size(); i++){v.push_back(m[nums1[i]]);}return v;}
};

下一個更大元素 II

給定一個循環數組，輸出每個元素的下一個更大元素。數字 x 的下一個更大的元素是按數組遍歷順序，這個數字之后的第一個比它更大的數。如果不存在，則輸出 -1。（題源力扣）

示例：

輸入： [1,2,1]
輸出： [2,-1,2]
解釋：

第一個 1 的下一個更大的數是 2；
數字 2 找不到下一個更大的數；
第二個 1 的下一個最大的數需要循環搜索，結果也是 2。

思路

因為我們要循環搜索，因此要么將數組拉直——復制所有元素并添加在數組尾部；要么假設數組長度為真正長度的二倍，并且遍歷的時候對長度取余，這里我們選擇后一種方法。并將遍歷分成正序遍歷和逆序遍歷兩種方法：

正序遍歷：

單調棧 st 用以記錄下標，正序遍歷給定的數組 nums，范圍為 [0, nums.size()-1] ，當前遍歷到的下標值為 i ，結果數組為 v ，結果數組數值全部被初始化為 -1。
當 棧不為空 且 棧頂下標對應的元素小于當前遍歷的元素 。
1. v[棧頂下標] = nums[i%n] ，棧頂下標對應的元素 的 下一個最大元素 即為 當前遍歷到的元素。
2. st.pop() ，彈出棧頂元素，單調棧遵循嚴格遞增規則。
當前遍歷到的元素其下標入棧，st.push(i%n)。由于每個元素都會被遍歷到并且被壓入棧中，而棧中每個元素都會被處理（沒有下一個最大元素的棧中元素直接被彈出，反之則匹配下一個最大元素）。

逆序遍歷：

單調棧 st 用以記錄元素值，逆序遍歷給定的數組 nums，范圍為 [nums.size()-1, 0] ，當前遍歷到的下標值為 i ，結果數組為 v ，結果數組數值全部被初始化為 -1。
當 棧不為空 且 棧頂元素小于等于當前遍歷的元素 。
1. st.pop() ，彈出棧頂元素，單調棧遵循嚴格遞增規則。
當 i < nums.size() 時，開始逆序更新結果數組的元素，在此之前對單調棧進行的更新只為解決 nums 最后一次降峰的元素（下例中的 5，4 ）單次遍歷無法匹配下一個更大元素的問題。以 2，3，6，4，5，4 為例：
1. 一次遍歷只能得到結果數組 3，6，-1，5，-1，-1。對于 5，4 兩個元素而言，無法正確匹配下一個更大元素，這也是和上一題的主要區別之所在。
2. 因此倘若我們將整個遍歷過程看作對 nums 的兩次遍歷，就會發現，第一次遍歷結果是單調棧中只有 6，也就是解決了無法正確匹配5，4 兩個元素的下一個更大元素，而第二次遍歷則是對最后一次降峰之前所有元素進行匹配下一個最大元素的操作。

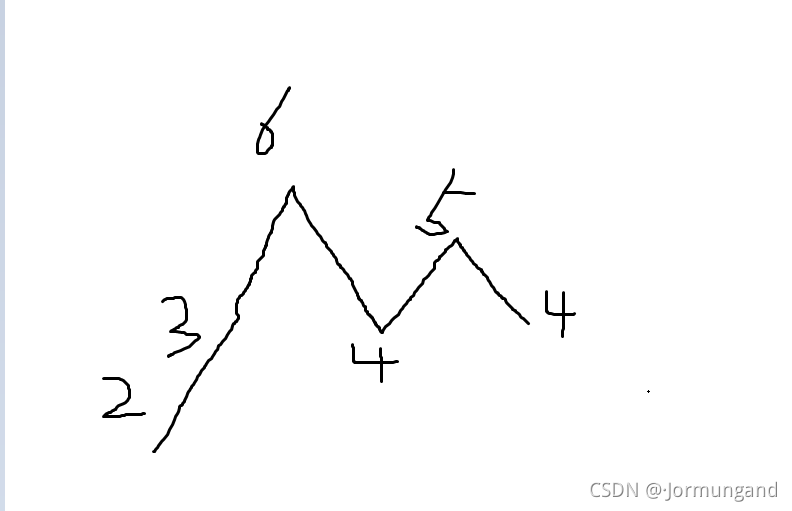
注：上面提到了降峰，這其實是對數組常見的稱呼方法，意為將數組元素以折線圖的形式表示看起來像一座座山峰，對于 2，3，6，4，5，4 而言，它們是形如下圖的兩座山峰：
在這里插入圖片描述

代碼

正序遍歷：

class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n = nums.size();vector<int> v(n, -1);stack<int> st;for(int i = 0; i < n*2; i++){int t = nums[i%n];while(st.size() && nums[st.top()]<t){v[st.top()] = t;st.pop();}st.push(i%n);//cout << nums[i%n] << " " << m[nums[i%n]] << endl;}return v;}
};

逆序遍歷：

class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n = nums.size();vector<int> v(n, -1);stack<int> st;for(int i = n*2-1; i >= 0; i--){int t = nums[i%n];while(st.size() && st.top()<=t) st.pop();if(i <= n-1) v[i] = st.empty() ? -1 : st.top();st.push(t);//cout << nums[i%n] << " " << m[nums[i%n]] << endl;}return v;}
};

132 模式

給你一個整數數組 nums ，數組中共有 n 個整數。132模式 的子序列由三個整數 nums[i]、nums[j] 和 nums[k] 組成，并同時滿足：i < j < k 和 nums[i] < nums[k] < nums[j] 。（題源力扣）

如果 nums 中存在 132模式 的子序列，返回 true ；否則，返回 false 。

示例：

輸入： nums = [1,2,3,4]
輸出： false
解釋： 序列中不存在 132 模式的子序列。

思路

單調棧 st 用以暫存可能為 132模式 中 2 的數據，遵循嚴格遞減規則，變量 sec 為真正的 2，將其初始化為 INT_MIN。
倒序遍歷數組，因為我們目的在于枚舉 2 ，而 2 必定從數組尾部優先出現，當前遍歷到的下標為 i 。
1. 當 nums[i] < sec ，確定了 1，返回 true 。
2. 當 棧不為空 且 當前遍歷到的元素大于棧頂元素 ，當前元素暫定為 3 ，更新 sec 代表的 2 。
3. 優化：當前遍歷到的元素大于 sec ，當前元素入棧。本條規則的依據是：如果 nums[i] ≤ sec，那么即使它在未來被彈出，也不會將 sec 更新為更大的值。
  - 為什么 將 sec 更新為更大的值 如此重要呢？因為 2 的值越大，那么我們之后找到 1 的機會也就越大。

代碼

class Solution {
public:bool find132pattern(vector<int>& nums) {int n = nums.size();stack<int> st; // 單調棧維護2st.push(nums[n-1]);int sec = INT_MIN; // second表示真正的2for(int i = n-2; i >= 0; i--){int t = nums[i];if(t < sec) return true; // 當前t作為1while(st.size() && t>st.top()){sec = st.top();st.pop();}if(t>sec) st.push(t); // 優化}return false;}
};

接雨水

給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之后能接多少雨水。

示例：

輸入： height = [0,1,0,2,1,0,1,3,2,1,2,1]
輸出： 6
解釋： 上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接 6 個單位的雨水（藍色部分表示雨水）。

思路

單調棧 st 遵循嚴格遞減規則，暫存可以作為 接水形狀左邊界的下標。用變量 res 保存能接多少雨水，正序遍歷數組 height：

當 棧不為空 且 當前遍歷到的元素大于棧頂下標對應的元素，表明有可能出現可接雨水的 “容器” 。
1. 將棧頂下標對應元素作為容器底部 bot，然后彈出，將新的棧頂下標作為容器左邊界 left。
2. 容器能容納的雨水為長 * 高 = i - left - 1 * (min(height[left], height[i]) - bot) ，解釋一下，長度為右邊界 i 和左邊界 left 的差值減一，高度為左邊界高度和右邊界高度中較小值與容器底部 bot 的差值，畢竟木桶接水的多少取決于最短的一塊木板。
其余情況則直接將 當前遍歷到的元素下標 壓入棧中，此時單調棧 st 遵循嚴格遞減規則。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();stack<int> st;int res = 0;for(int i = 0; i < n; i++){int t = height[i];while(st.size() && height[st.top()]<t){int bot = height[st.top()];//cout << "left: " << left << endl;st.pop();if(st.size()){int left = st.top();res += (i-left-1)*(min(t, height[left])-bot);}}st.push(i);}return res;}
};