---

最長相等前后綴

給出一個字符串 ababa

前綴集合：{a, ab, aba, abab}

后綴集合：{a, ba, aba, baba}

相等前后綴 即上面用同樣顏色標識出來的集合元素，最長相等前后綴 也就是所有 相等前后綴 中最長的那一個，也就是上面的 aba 。用圖片舉例：

最長相等前后綴 就是 KMP 算法滑動的依據。我們用 next 數組存儲 最長相等前后綴，以避免每次需要用到 最長相等前后綴 時都需要遍歷尋找的繁瑣。

---

next數組

概念

next[i]=j 的含義是：下標 i 之前的字符串其 最長相等前后綴 的長度為 j 。next[0]= -1 （前面沒有字符串單獨處理）。

a	b	a	b	a	c	d
next[0] = -1	next[1] = 0	next[2] = 0	next[3] = 1	next[4] = 2	next[5] = 3	next[6] = 0

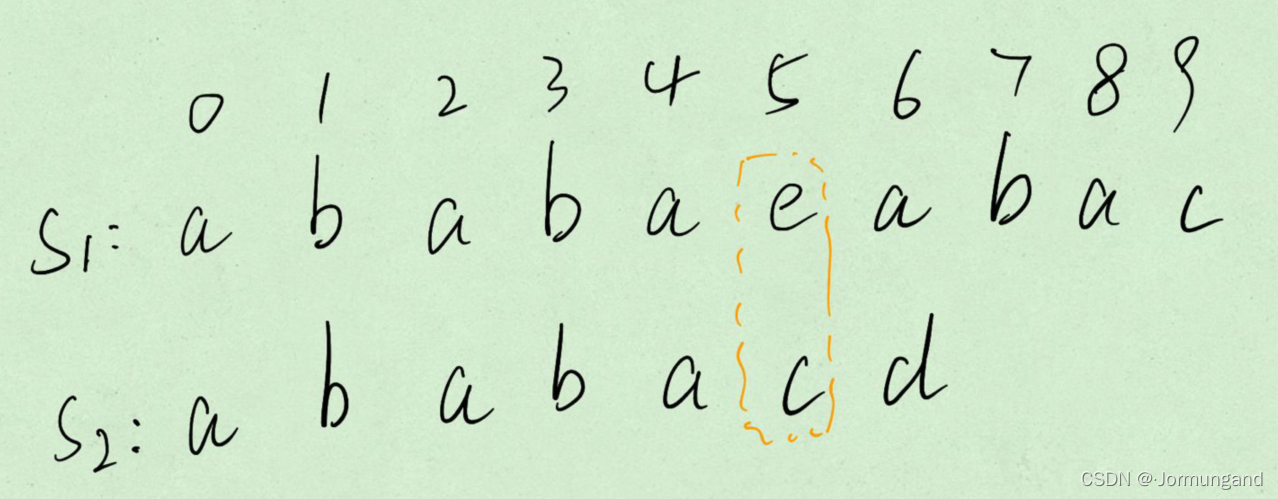
當 s1[5] != s2[5] 時，移動 s2，讓 s2 的前綴（ababa）匹配 s1 的后綴（ababa），即比較 s1[5] 和 s2[next[5]] 。移動的距離是 不匹配位置下標 和 相等前綴 之間的字符數量，即 5-3=2 。

從上面的例子中可以看出，next 的作用有兩個：

1. 表示該處字符不匹配時應該回溯到的字符的下標。
2. 上文提到的：下標 i 之前的字符串其 最長相等前后綴 的長度。

---

代碼實現

class Solution {public:void GetNext(const string& s, vector<int>& next) {int i = 0, j = -1;next[0] = -1; // 下標為0的字符前沒有字符串while (i < next.size() - 1) { // 因為函數體中每次先對i++，再對next[i]進行賦值// 因此i需要小于next.size() - 1，以保證自增時不越界if (j == -1 || s[i] == s[j]) {i++;j++; /* 關于 j *//*s[i] == s[j]成立時，next[i] 在 next[i - 1] 的值(j)的基礎上 + 1換言之，也就意味著相等前后綴的長度+1，新后綴結尾 i+1 對應的前綴結尾為 j+1*//* j == -1成立時，說明不存在相等前后綴，因此 i 之前的字符串的相等前后綴長度為 next[i] = (-1)++ = 0 */ next[i] = j;}else {j = next[j];// next[j] 是回溯的位置，是 j 指向的字符 之前的字符串的最長相等前后綴的長度// 該操作為了將前綴移動到后綴的位置上，假設 相等長度為 m// 相當于將 (0, j-m)、(1, j-m+1)...(m-1, j-1)匹配上// 舉個例子：// 字符串：a  b a b a c d// next：  -1 0 0 1 2 3//                j   i// 由于 j 指向的 字符b 其之前的 字符串 aba 最長相等前后綴的長度為 1，// 下標1 作為 新j 就將(0, j-1)匹配上了// 換言之，只需要將 下標1 作為 新j 即可將求 ababac 最長相等前后綴問題轉換為// 求 abac 最長相等前后綴的問題。}}}void getNext(const string& pattern, vector<int>& next){ // 另一種寫法int i, j = 0;next[0] = -1;   //第一個位置不存在數據，為-1for (int i = 1; i < next.size(); i++){//如果當前位置沒有匹配前綴，則回溯到求當前后綴的最長可匹配前綴while (j != 0 && pattern[j] != pattern[i]){j = next[j];}//如果該位置匹配，則在next數組在上一個位置的基礎上加一if (pattern[j] == pattern[i]){j++;}next[i] = j;}}
};

關于提到的另一種寫法，這里不多做分析，可以閱讀凌桓大佬的博客。

---

圖解GetNext中的回溯

舉個直觀的例子：

• 紅色部分分別為：最長相等前、后綴。

• 藍色部分為雙指針指向的，待匹配的元素。

• 黑色部分為未開始匹配的部分。

• 綠色部分為 next 數組。
  

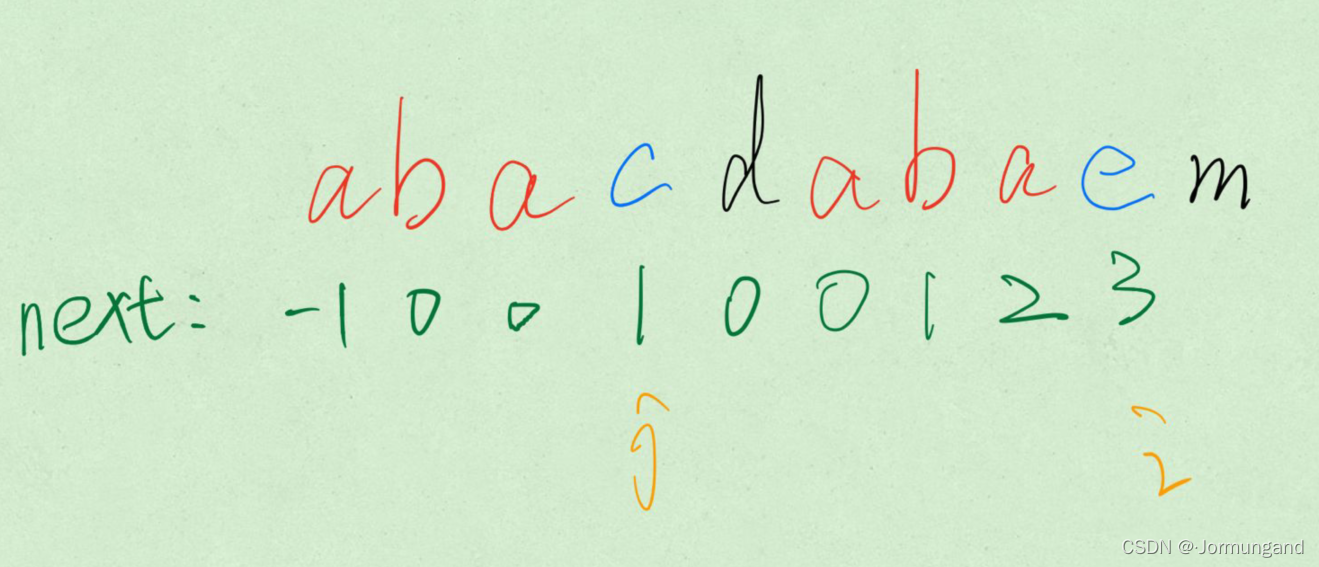
• 如果 s[i] == s[j] ，雙指針同時后移，紅色區域變大。

• 如果不匹配，必須在 紅色部分 重新尋找 相等前后綴，新的相等前后綴長度必然縮短。

紫色部分是紅色部分的最長相等前后綴，可以看到，四個紫色部分都是完全相等的。同時，改變 j 的指向，回溯后 j = next[j] ：

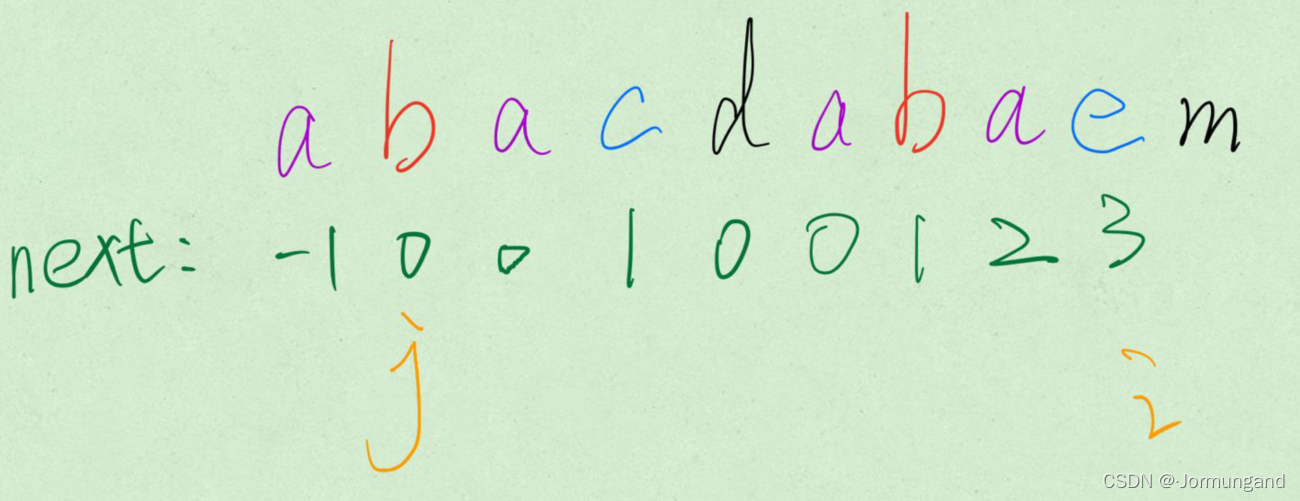
1. 此時，若 s[i] == s[j]，又因 j 前面的紫色部分和 i 前面的紫色部分完全相等。則最長相等前后綴長度+1。
2. 不等則進行下一次回溯。圖中下一次回溯時不再有相等前后綴，因此不再有紫色部分，不斷地回溯，直到 j 指向 -1，此時觸發判定條件，執行 j++; i++; next[i]=j; 。

---

改進

舉個例子：

• 主串 s = “aaaabaaaaac”
• 子串 t = “aaaac”

當 b 與 c 不匹配時應該 b 與下標為 next[c] = 3 的元素 a 比，這顯然是不匹配的，繼續回溯，next[next[c]] 回溯后的字符依然是 a 。此時已經 沒有必要再將進行回溯了。

節省效率的做法應該是當 b 和 next[3] 不匹配時，就直接回溯到首個 a 的 next 指向（即下標 -1）。即：

下標	0	1	2	3	4
元素	a	a	a	a	c
next	-1	0	1	2	3
fail	-1	-1	-1	-1	3

規則：

• 如果 i 位字符與它 next 值指向的 j 位字符相等，則該 i 位的 fail 就指向 j 位的 fail 值；
• 如果不等，則該 i 位的 fail 值就是它自己的 next 值。

舉個其他例子 ababaaab，進一步體會：

下標	0	1	2	3	4	5	6	7
元素	a	b	a	b	a	a	a	b
next	-1	0	0	1	2	3	1	1
fail	-1	0	-1	0	-1	3	1	0

---

代碼實現

這里用 next 表示上面提到的 fail 數組。

void getNext(const string& s, vector<int>& fail) {int i = 1, j = 0;fail[0] = -1; // 下標為0的字符前沒有字符串while (i < fail.size()) {if (s[i] != s[j]) { // 字符不匹配fail[i] = j; // 不等時，fail[i] = next[i] = jj = fail[j]; // 回溯}else { // 字符匹配fail[i] = fail[j]; // i 指向的字符與 j 指向字符相等}j++;i++;}
}

輸出結果：

---

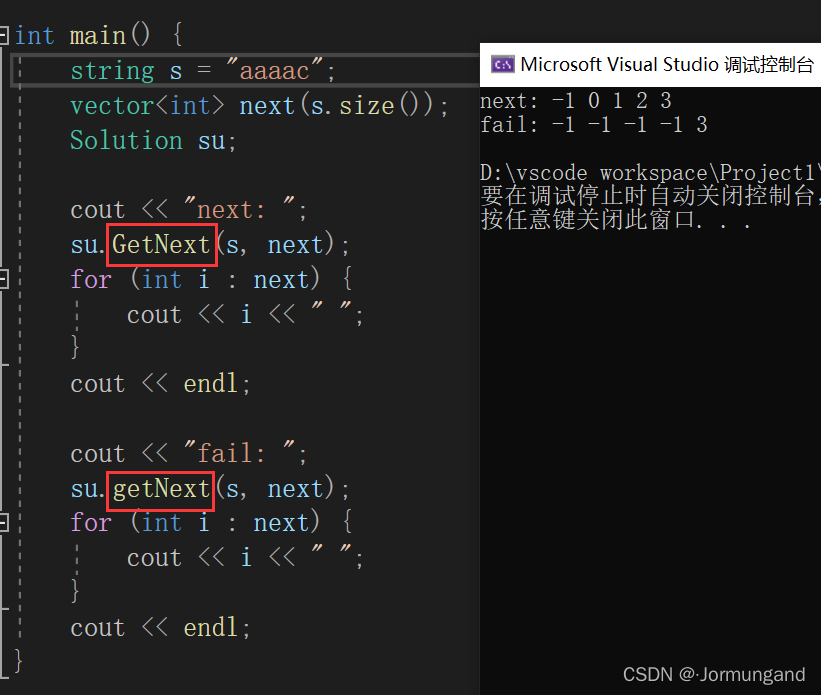
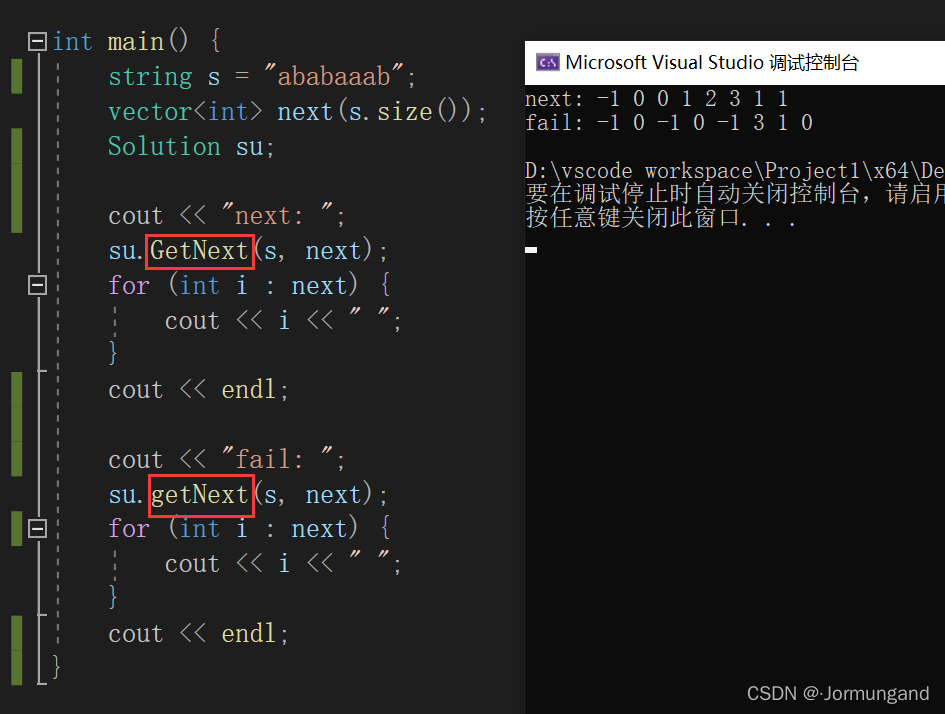
代碼

class Solution {
public:void GetNext(const string& s, vector<int>& next) {int i = 0, j = -1;next[0] = -1; // 下標為0的字符前沒有字符串while (i < next.size()-1) { if (j == -1 || s[i] == s[j]) {i++;j++;next[i] = j;}else {// 如果當前位置沒有匹配前綴，則回溯到求當前后綴的最長可匹配前綴j = next[j];}}}void getNext(const string& s, vector<int>& fail) { // 改進的next數組int i = 1, j = 0;fail[0] = -1; // 下標為0的字符前沒有字符串while (i < fail.size()) {if (s[i] != s[j]) { // 字符不匹配fail[i] = j; // 不等時，fail[i] = next[i] = jj = fail[j]; // 回溯}else { // 字符匹配fail[i] = fail[j]; // i 指向的字符與 j 指向字符相等}j++;i++;}}int knuthMorrisPratt(const string& query, const string& pattern) {//不滿足條件則直接返回falseif (query.empty() || pattern.empty() || query.size() < pattern.size()){return -1;}int i = 0, j = 0;int len1 = query.size(), len2 = pattern.size();vector<int> next(pattern.size(), -1); // next數組GetNext(pattern, next);while (i < len1 && j < len2){if (j == -1 || query[i] == pattern[j]){i++;j++; // i、j各增1}else j = next[j]; // i不變，j回溯}if (j == len2)return(i - len2); // 返回匹配模式串的首字符下標elsereturn -1; // 返回不匹配標志}
};

---

復雜度分析

• 空間復雜度O(M)： 需要借助到一個 next 數組，數組長度為 $M$，$M$ 為模式串長度。
• 時間復雜度O(N + M)： 時間復雜度主要包含兩個部分，next 數組的構建以及對主串的遍歷：next 數組構建的時間復雜度為 O(M)；后面匹配中主串不回溯，循環時間復雜度為 O(N)，所以 KMP 算法的時間復雜度為 O(N + M)。