---

題目

給出一組數據 nums，求出其最長下降子序列（子序列允許不連續）的長度。（類似于lc的最長遞增子序列）

示例：

輸入：

6 // 數組元素個數
3 4 3 5 2 1 // 數組

輸出：

4 // 最長下降子序列為4321，長度為4

---

解法

DP+暴搜

思路

DP數組 表示 nums數組 對應下標的元素作為末尾時最長下降子序列的長度，因此將 DP數組中的元素 全部初始化為 1（最起碼這個下降子序列里有當前元素）。

從 nums 的第二個元素開始（記為 i），向前搜索所有大于它的元素（記為 j），找到后 dp[i] = max(dp[i], dp[j] + 1) 。舉個例子會更直觀：

nums = 3 4 3 5 2 1
dp =   1 1 2 1 3 4?形成下降子序列：4,3   

在 i=4, nums[i]=2 時，這個狀態轉移方程顯得尤為重要：

• 從 j=0 開始遍歷，第一個大于 2 的元素是 j=1, nums[j]=4 ，dp[i]=dp[j]+1=2，意味著可以形成下降子序列：4,2，長度為 dp[i]=2；
• 第二個大于 2 的元素是 j=2, nums[j]=3 ，dp[i]=dp[j]+1=3，意味著可以形成下降子序列：4,3,2
• 第三個大于 2 的元素是 j=3, nums[j]=5 ，dp[i]=dp[i]=3，意味著形成 5,2 不如形成 4,3,2 更長，所以仍保持原來的下降子序列。

值得注意的是最長下降子序列的長度是 DP數組 中最大的元素而非尾元素，舉個例子：

nums = 3 4 3 5 2 3
dp =   1 1 2 1 3 2

因此在構建 DP數組 的同時要記得保存最大元素哦~

代碼實現

int main() {int n, res = 1;cin >> n;vector<int> v(n), dp(n, 1);for (int i = 0; i < n; i++) {cin >> v[i];}for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (v[j] > v[i]) dp[i] = max(dp[j] + 1, dp[i]);}res = max(dp[i], res);}cout << res << endl;
}

---

貪心+二分

思路

dp數組： 用來暫存一個 下降子序列，注意，這里的序列并非真正的最長下降子序列，至于原因下文解釋。由于題目要求的是最長下降子序列的長度，并不用返回序列的具體排列，因此dp數組的長度就是本題的答案。

該方法思路分三步：請客、斬首、收下當狗。

1. 請客：遍歷 數據數組 中每個元素，和 dp數組 的尾元素比較。
2. 收下當狗：如果比較結果是當前遍歷到的元素小于 dp數組 尾元素，則當前元素直接加入 dp數組，成為新的尾元素。
3. 斬首：斬 dp數組 中舊元素的首，當前遍歷到的元素作為新元素，自然要先收下當狗，具體做法是：
   • 通過二分法找到 dp數組 中所有小于當前元素中最大的那個，用當前元素替換掉它。舉個例子，比如：dp數組元素是 9，5，3，1。當前遍歷到的元素是 6，那么dp數組會變成：9，6，3，1。

為什么說 dp數組 暫存的下降子序列只是和真正的最長下降子序列長度相等，兩者內容并不一樣？

原因就在于第3點——斬首，斬首的目的是 在不改變子序列長度的基礎上擴大下降子序列的最小值，用具體例子來說明：

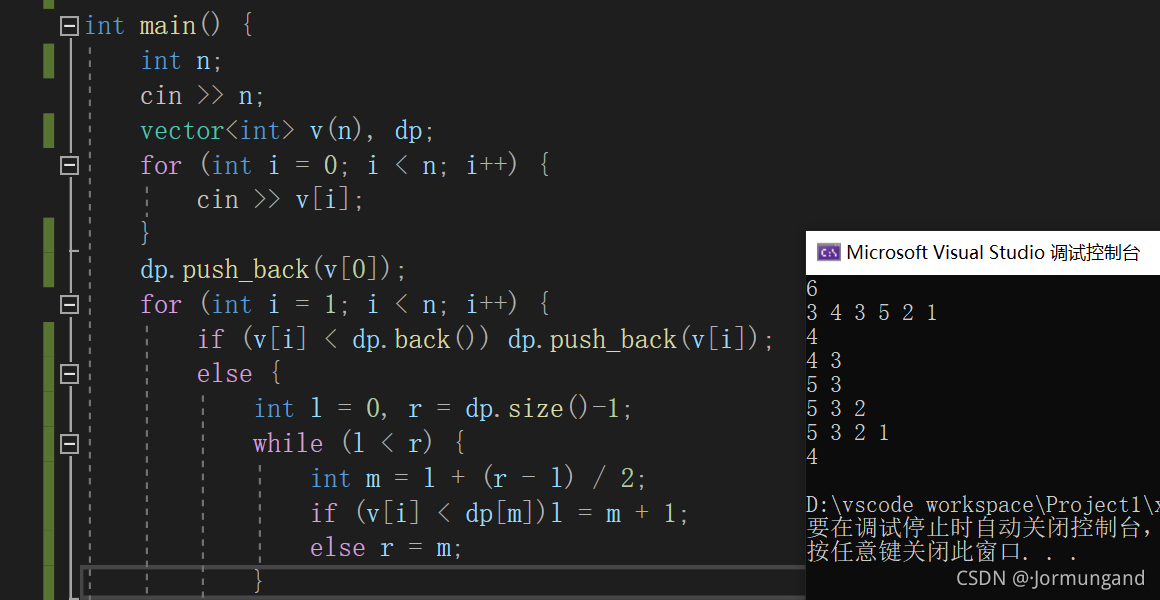
假如給出的數據是 3，4，3，5，2，1。那么 dp數組 的變化會是：

dp數組內容	當前遍歷到的元素	最長下降子序列 ｜
3	3	3
4	4	4 或 3
4,3	3	4,3
5，3	5	4，3
5，3，2	2	4，3，2
5，3，2，1	1	4，3，2，1

代碼實現

int main() {int n;cin >> n;vector<int> v(n), dp;for (int i = 0; i < n; i++) {cin >> v[i];}dp.push_back(v[0]);for (int i = 1; i < n; i++) {if (v[i] < dp.back()) dp.push_back(v[i]);else {int l = 0, r = dp.size()-1;while (l < r) {int m = l + (r - l) / 2;if (v[i] < dp[m])l = m + 1;else r = m;}dp[l] = v[i];}for (int j : dp) {cout << j << " ";}cout << endl;}cout << dp.size() << endl;
}