一、AVL樹的定義

AVL樹，全稱 平衡二叉搜索（排序）樹。

二叉搜索樹雖可以縮短查找的效率，但如果數據有序或接近有序二叉搜索樹將退化為單支樹，查找元素相當于在順序表中搜索元素，效率低下。因此，兩位俄羅斯的數學家G.M.Adelson-Velskii和E.M.Landis在1962年發明了一種解決上述問題的方法：當向二叉搜索樹中插入新結點后，如果能保證每個結點的左右子樹高度之差的絕對值不超過1(需要對樹中的結點進行調整)，即可降低樹的高度，從而減少平均搜索長度。

平衡因子（Balance Factor，簡寫為bf）
平衡因子（bf）：結點的左子樹的深度減去右子樹的深度。也可以是右子樹的深度減去左子樹的深度。看個人實現而異。

即： 結點的平衡因子 = 左子樹的高度 - 右子樹的高度。
或者 節點的平衡因子 = 右子樹的高度 - 左子樹的高度。

AVL樹本質上是一顆二叉查找樹，但是它又具有以下特點：

• 它的左右子樹都是AVL樹
• 左右子樹高度之差(簡稱平衡因子)的絕對值不超過1(-1/0/1)

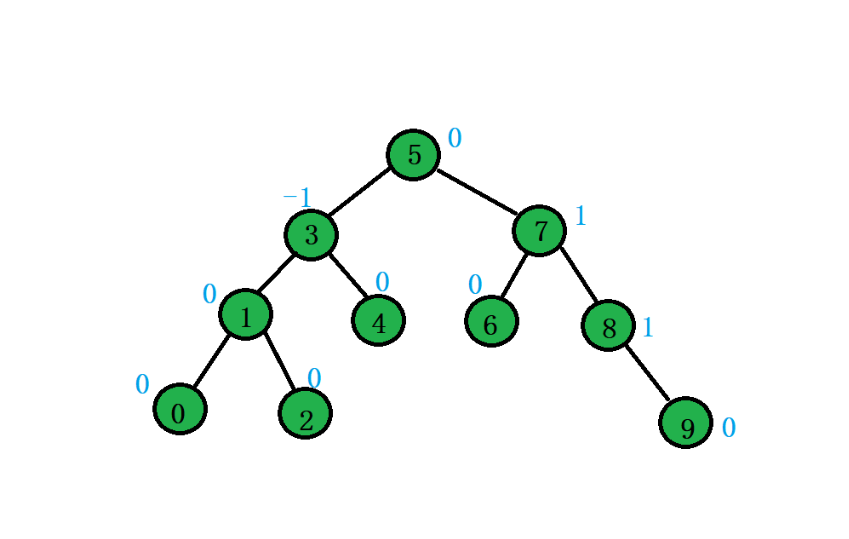
這就是一顆AVL樹

二、AVL樹的作用

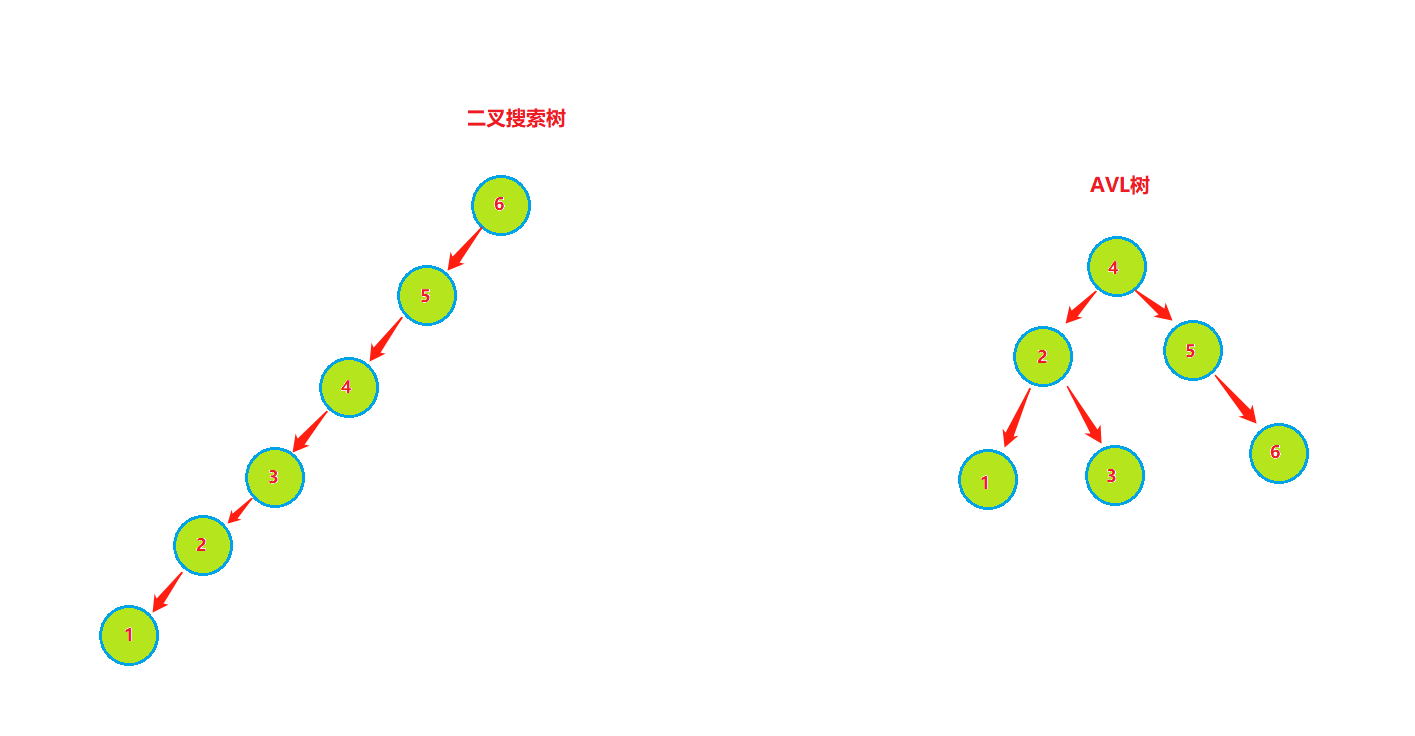
有一顆二叉樹，他有n個節點，如果他是一顆二叉搜索樹，他形狀多樣，可能會形成單枝樹，高度為n,那么在這顆搜索樹中查找元素的最壞時間復雜度為O(n),最好時間復雜度是O($lo{g}_{2}n$)。
如果他是一顆AVL樹，他的高度穩定為$lo{g}_{2}n$,查找元素的時間復雜度為O($lo{g}_{2}n$)。
由上圖可知，同樣的結點，由于插入方式不同導致樹的高度也有所不同。特別是在帶插入結點個數很多且正序的情況下，會導致二叉樹的高度是O(N)，而AVL樹就不會出現這種情況，樹的高度始終是O(lgN).高度越小，對樹的一些基本操作的時間復雜度就會越小。這也就是我們引入AVL樹的原因。

三、AVL樹的插入操作

插入——平衡因子的更新

在插入一個元素的時候，必然會引起平衡因子的變化，所以我們需要在插入的時候把平衡因子同時更新，在平衡因子大于1或者小于-1時，我們則需要進行旋轉操作，進行調整，使平衡因子再次正常，從而保證這顆二叉樹一直是一顆AVL樹。
?
使用平衡因子計算： 右子樹高度 - 左子樹高度

情況一：

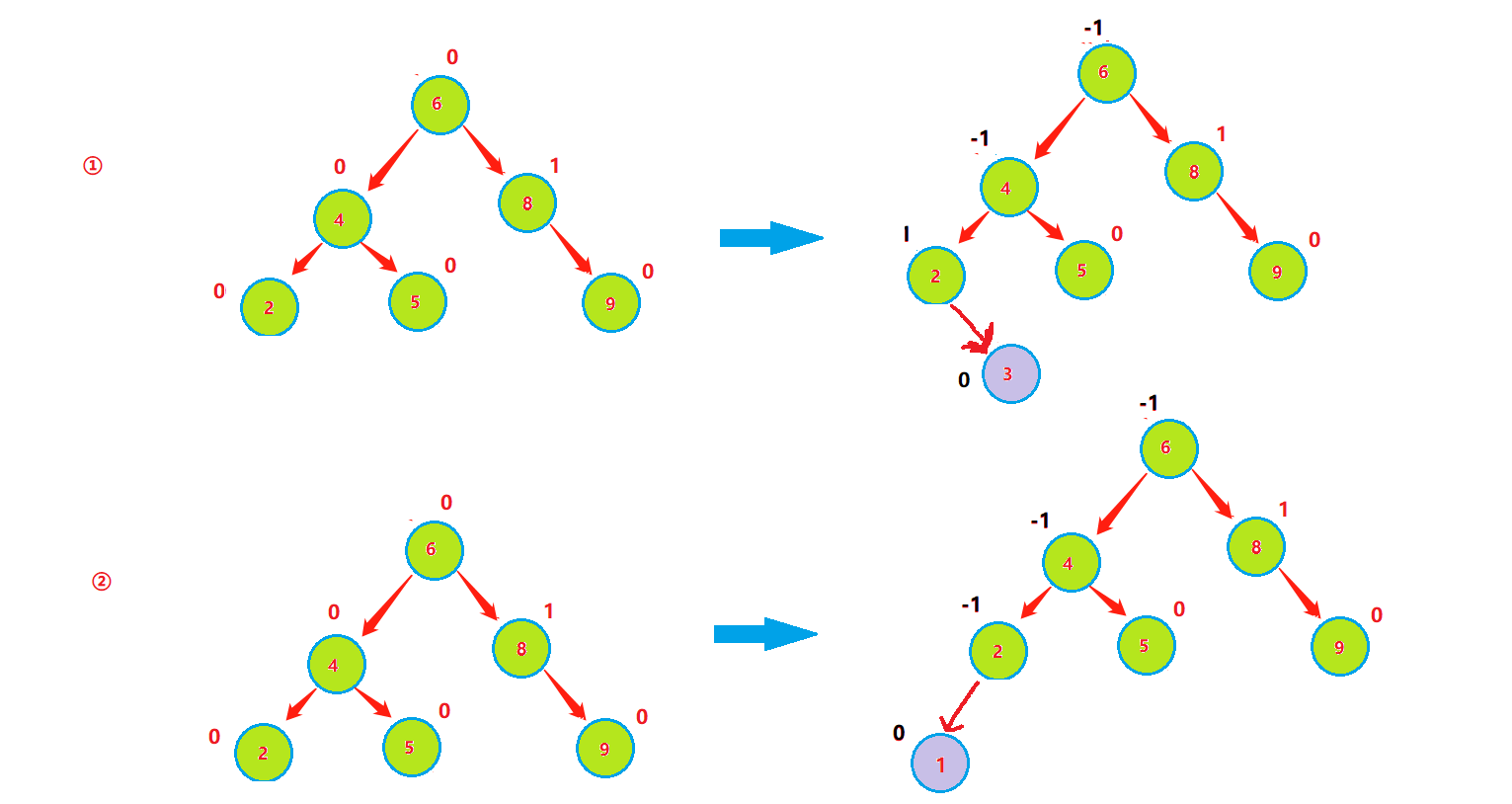
在插入元素后，需要更新父節點的平衡因子，在父節點的左子樹插入元素，父節點的平衡因子-1，在父節點的左子樹插入元素，父節點的平衡因子+1，如果父節點的平衡因子更新過后變為1或者-1，則需繼續往上更新至根節點，因為1或者-1表示該節點的高度發生改變，需往上更新。

情況2：

在插入元素后，需要更新父節點的平衡因子，在父節點的左子樹插入元素，父節點的平衡因子-1，在父節點的左子樹插入元素，父節點的平衡因子+1，如果父節點的平衡因子更新過后變為0，則不需要繼續向上更新，因為變為0只能說明該樹高度沒有變化，只是相對于原來變得平衡。

如果在更新平衡因子后，平衡因子不在(-1/0/1)范圍時，則需旋轉操作，下面講解如何進行旋轉操作

由于插入需要旋轉的情況較多，大致可以分為四大類

插入——左單旋

動圖演示

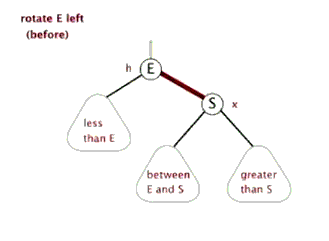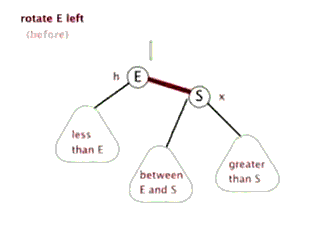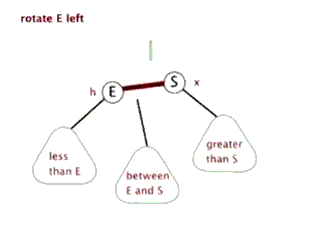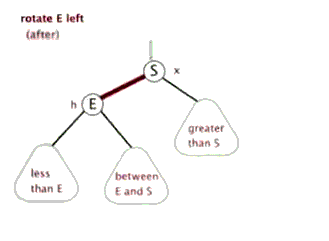
情況一
右子樹高時，在右子樹的右側插入元素，此時需要左單旋

插入——右單旋

動圖演示

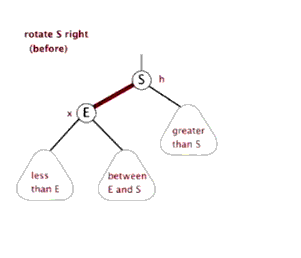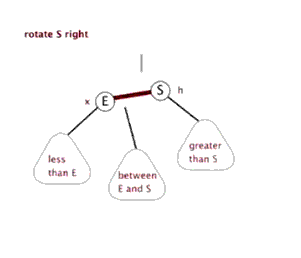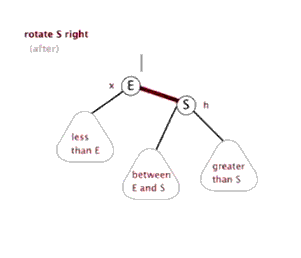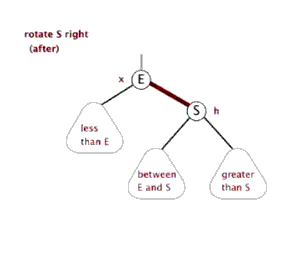
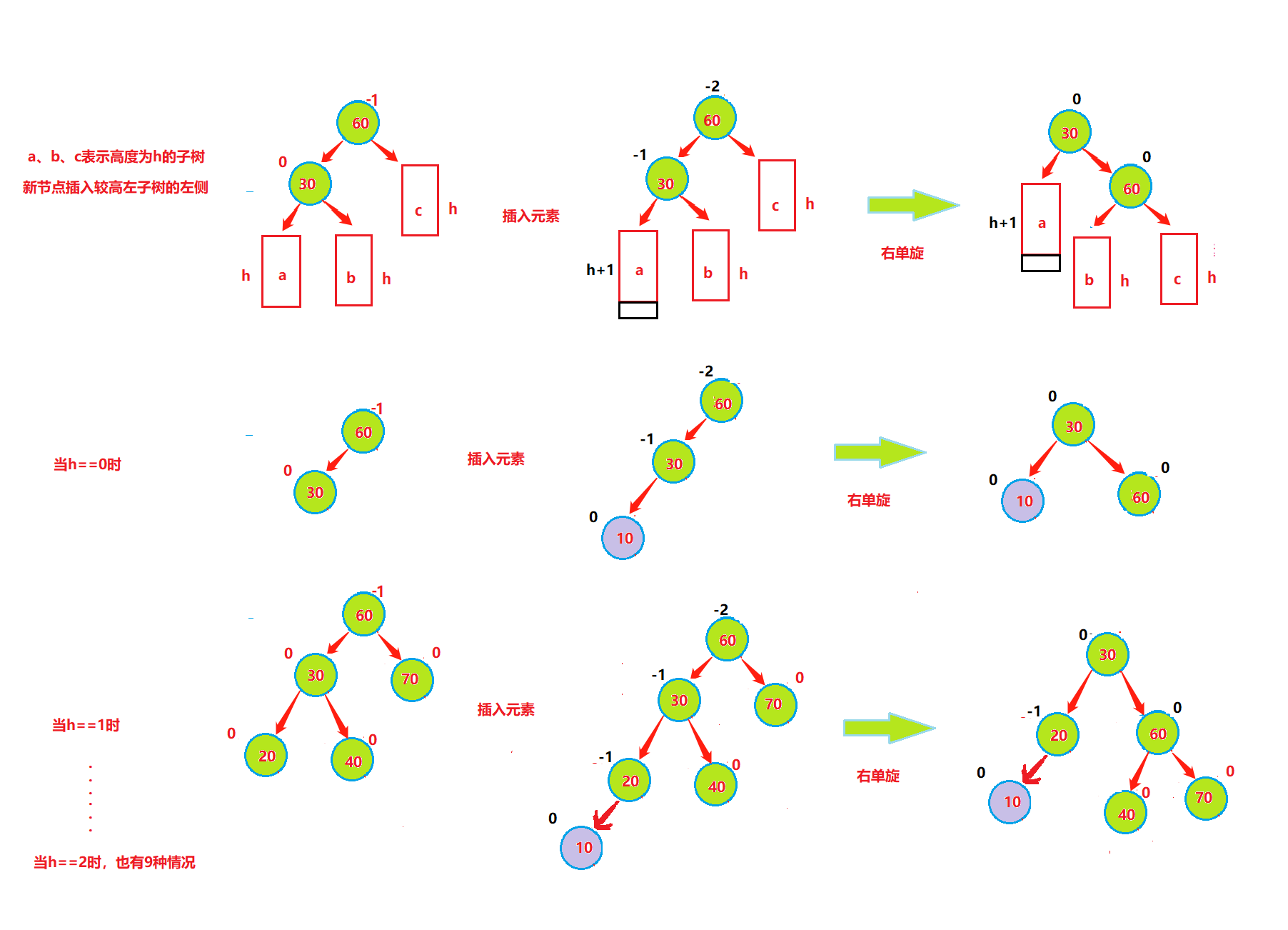
情況二、
左子樹較高時，在左子樹的左側插入元素，此時需要右單旋

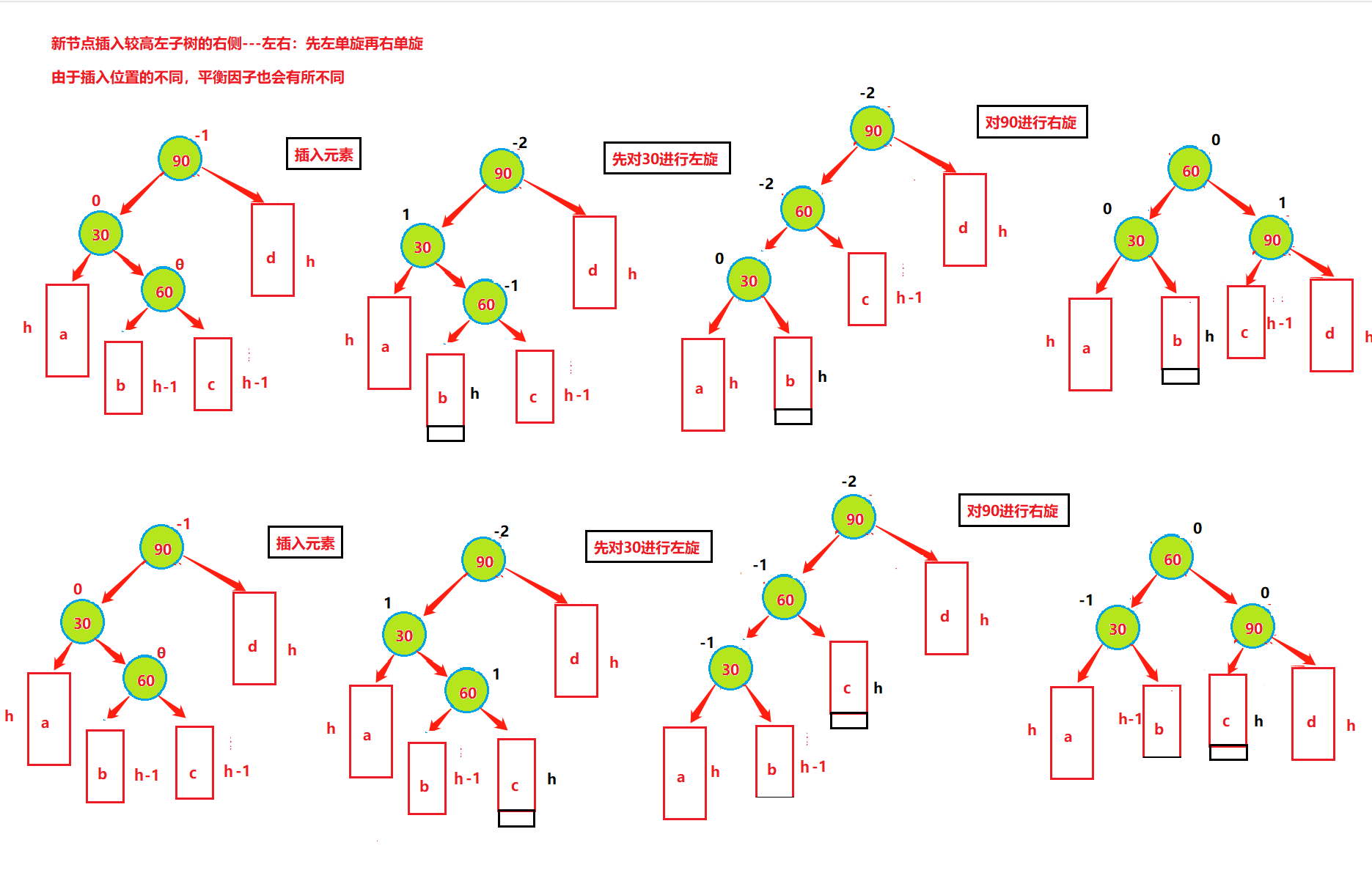
插入——左右雙旋

情況三、左子樹較高時，在左子樹的右側插入元素，此時需要左右雙旋，即：先對30進行左單旋，然后再對90進行右單旋

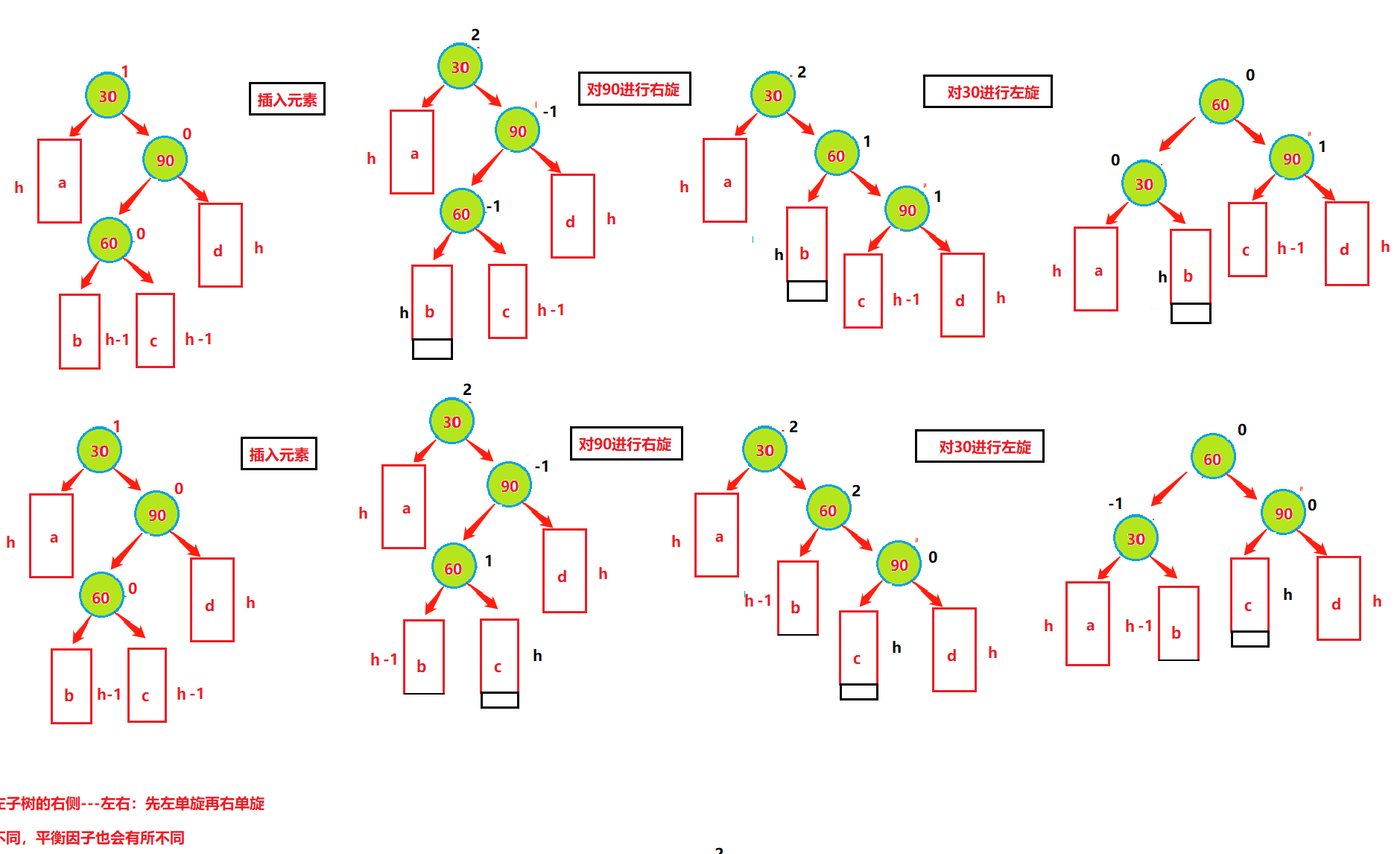
插入——右左雙旋

情況四、右子樹較高時，在右子樹的左側插入元素，此時需要右左雙旋，即：先對90進行右單旋，然后再對30進行左單旋

四、ALVL樹的驗證

int _Height(Node* root)
{//用來計算二叉樹的高度if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;
}bool _IsBalance(Node* root)
{if (root == NULL)return true;int leftH = _Height(root->_left);int rightH = _Height(root->_right);//檢查平衡因子if (rightH - leftH != root->_bf){cout << root->_kv.first << "節點平衡因子異常" << endl;return false;}//通過計算左右子樹的高度差判斷這顆二叉樹是否為AVL樹return abs(leftH - rightH) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);//檢查高度差要檢查二叉樹中所有節點的左右子樹的高度差
}bool IsBalance()
{return _IsBalance(_root);
}

五、AVL樹的性能

AVL樹是一棵絕對平衡的二叉搜索樹，其要求每個節點的左右子樹高度差的絕對值都不超過1，這樣可以保證查詢時高效的時間復雜度，即 $lo{g}_{2}n$ 。

但是如果要對AVL樹做一些結構修改的操作，性能非常低下，比如：插入時要維護其絕對平衡，旋轉的次數比較多，更差的是在刪除時，有可能一直要讓旋轉持續到根的位置。因此：如果需要一種查詢高效且有序的數據結構，而且數據的個數為靜態的(即不會改變)，可以考慮AVL樹，但一個結構經常修改，就不太適合。