
一、說明
1.1 介紹
????????貝葉斯推理是統計學中的一個主要問題,在許多機器學習方法中也會遇到。例如,用于分類的高斯混合模型或用于主題建模的潛在狄利克雷分配都是在擬合數據時需要解決此類問題的圖形模型。
????????同時,可以注意到,貝葉斯推理問題有時很難解決,具體取決于模型設置(假設、維數等)。在大型問題中,精確的解決方案確實需要大量的計算,而這些計算往往變得難以解決,并且必須使用一些近似技術來克服這個問題并構建快速且可擴展的系統。
????????在這篇文章中,我們將討論可用于解決貝葉斯推理問題的兩種主要方法:馬爾可夫鏈蒙特卡洛(MCMC),這是一種基于采樣的方法,以及變分推理(VI),這是一種基于近似的方法。
1.2 大綱
????????在第一部分中,我們將討論貝葉斯推理問題,并看到一些經典機器學習應用程序的示例,其中自然會出現此問題。然后在第二部分中,我們將介紹全球MCMC技術來解決這個問題,并提供有關兩種MCMC算法的一些詳細信息:Metropolis-Hasting和Gibbs Sampling。最后,在第三部分中,我們將介紹變分推理,并了解如何在參數化分布族上進行優化過程后獲得近似解。
注意。用(∞)標記的小節非常數學,可以跳過而不會損害對這篇文章的全球理解。另請注意,在這篇文章中,p(.) 用于表示概率、概率密度或概率分布,具體取決于上下文。
二、貝葉斯推理問題
????????在本節中,我們將介紹貝葉斯推理問題并討論一些計算困難,然后給出潛在狄利克雷分配的例子,這是一種遇到此問題的主題建模的具體機器學習技術。
2.1 什么是推理?
????????統計推斷包括根據我們觀察到的內容來了解我們沒有觀察到的東西。換句話說,它是根據該總體或該總體樣本中的一些觀察到的變量(通常是效應)得出結論的過程,例如關于總體中某些潛在變量(通常是原因)的準時估計、置信區間或分布估計。
????????特別是,貝葉斯推理是采用貝葉斯觀點產生統計推斷的過程。簡而言之,貝葉斯范式是一種統計/概率范式,其中每次記錄新的觀察時,都會更新由概率分布建模的先驗知識,其不確定性由另一個概率分布建模。支配貝葉斯范式的整個思想嵌入在所謂的貝葉斯定理中,該定理表達了更新的知識(“后驗”),先驗知識(“先驗”)和來自觀察的知識(“可能性”)之間的關系。
????????一個經典的例子是參數的貝葉斯推理。讓我們假設一個模型,其中數據 x 是根據未知參數 θ 從概率分布生成的。我們還假設我們對參數 θ 有先驗知識,可以表示為概率分布 p(θ)。然后,當觀察到數據 x 時,我們可以使用貝葉斯定理更新有關此參數的先驗知識,如下所示

貝葉斯定理應用于給定觀測數據的參數推斷的圖示。
2.2 計算困難
????????貝葉斯定理告訴我們,后驗的計算需要三個項:先驗、可能性和證據。前兩個可以很容易地表達,因為它們是假設模型的一部分(在許多情況下,先驗和可能性是明確已知的)。但是,第三項,即歸一化因子,需要計算如下:

????????雖然在低維中可以毫不費力地計算這個積分,但在高維中它可能變得棘手。在最后一種情況下,后驗分布的精確計算實際上是不可行的,必須使用一些近似技術來獲得需要知道該后驗的問題的解決方案(例如平均計算)。
????????我們可以注意到,貝葉斯推理問題可能會產生一些其他計算困難,例如,當某些變量是離散的時,組合數學問題。在最常用于克服這些困難的方法中,我們發現馬爾可夫鏈蒙特卡羅和變分推理方法。在這篇文章的后面,我們將描述這兩種方法,特別關注“歸一化因子問題”,但應該記住,當面對與貝葉斯推理相關的其他計算困難時,這些方法也很寶貴。
????????為了使接下來的章節更加通用,我們可以觀察到,由于 x 應該被給出并且可以作為參數進行,因此我們面臨著這樣一種情況:我們在 θ 上定義了一個概率分布,直到一個歸一化因子。
![]()
????????在接下來的兩節中描述MCMC和VI之前,讓我們舉一個使用潛在狄利克雷分配的機器學習中的貝葉斯推理問題的具體示例。
2.3 例
????????貝葉斯推理問題自然會出現,例如,在假設概率圖模型的機器學習方法中,并且給定一些觀察結果,我們希望恢復模型的潛在變量。在主題建模中,潛在狄利克雷分配(LDA)方法為語料庫中的文本描述定義了這樣的模型。因此,給定大小為 V 的完整語料庫詞匯表和給定數量的主題 T,該模型假設:
- 對于每個主題,詞匯表上都存在“主題-詞”概率分布(假設先驗狄利克雷)
- 對于每個文檔,存在主題上的“文檔-主題”概率分布(假設另一個狄利克雷先驗)
- 文檔中的每個單詞都經過采樣,首先,我們從文檔的“文檔-主題”分布中抽取了一個主題,其次,我們從附加到采樣主題的“主題-單詞”分布中抽取了一個單詞
????????該方法的名稱來自模型中假設的狄利克雷先驗,其目的是推斷觀察到的語料庫中的潛在主題以及每個文檔的主題分解。即使我們不深入研究LDA的細節,我們也可以非常粗略地說,表示語料庫中單詞的向量w和與這些單詞相關的主題向量,我們希望根據觀察到的w以貝葉斯方式推斷z:
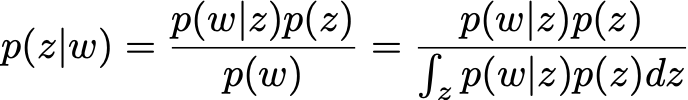
????????在這里,除了歸一化因子由于維度巨大而絕對難以處理這一事實之外,我們還面臨著一個組合挑戰(因為問題的某些變量是離散的),需要使用MCMC或VI來獲得近似解。對主題建模及其特定的潛在貝葉斯推理問題感興趣的讀者可以看看這篇關于LDA的參考論文。

潛在狄利克雷分配方法圖示。
三、馬爾可夫鏈蒙特卡洛 (MCMC)
? ? ? ? MCMC的意義是:Markov Chains Monte Carlo (MCMC)。
????????正如我們之前提到的,處理貝葉斯推理問題時面臨的主要困難之一來自歸一化因子。在本節中,我們描述了MCMC采樣方法,這些方法構成了克服此問題的可能解決方案,以及與貝葉斯推理相關的其他一些計算困難。
3.1 抽樣方法
????????抽樣方法的思路如下。讓我們首先假設我們有一種方法(MCMC)從定義為因子的概率分布中提取樣本。然后,我們不必嘗試處理涉及后驗的棘手計算,而是可以從該分布中獲取樣本(僅使用未歸一化的部分定義),并使用這些樣本來計算各種準時統計量,例如均值和方差,甚至通過核密度估計近似分布。
????????與下一節中描述的VI方法相反,MCMC方法假設所研究的概率分布沒有模型(貝葉斯推理案例中的后驗)。因此,這些方法具有低偏差但高方差,這意味著大多數時候獲得結果的成本更高,但也比我們從VI中獲得的結果更準確。
????????為了結束這一小節,我們再次概述了這樣一個事實,即我們剛剛描述的這個抽樣過程不限于后驗分布的貝葉斯推斷,并且更一般地說,還可以用于概率分布定義為其歸一化因子的任何情況。

抽樣方法(MCMC)的圖示。
3.2 MCMC的理念
????????在統計學中,馬爾可夫鏈蒙特卡羅算法旨在從給定的概率分布中生成樣本。該方法名稱的“蒙特卡洛”部分是由于采樣目的,而“馬爾可夫鏈”部分來自我們獲取這些樣本的方式(我們請讀者參考我們關于馬爾可夫鏈的介紹性文章)。
????????為了產生樣本,我們的想法是建立一個馬爾可夫鏈,其平穩分布是我們想要從中采樣的分布。然后,我們可以模擬來自馬爾可夫鏈的隨機狀態序列,該序列足夠長(幾乎)達到穩定狀態,然后保留一些生成的狀態作為我們的樣本。
????????在隨機變量生成技術中,MCMC是一種非常先進的方法(我們已經在關于GAN的文章中討論了另一種方法),它可以從非常困難的概率分布中獲取樣本,該概率分布可能僅定義到乘法常數。使用MCMC,我們可以從未很好地歸一化的分布中獲得樣本,這是一個違反直覺的事實是,我們定義馬爾可夫鏈的特定方式對這些歸一化因子不敏感。

馬爾可夫鏈蒙特卡羅方法旨在從困難的概率分布中生成樣本,該概率分布可以定義為一個因子。
3.3 馬爾可夫鏈的定義
????????整個MCMC方法基于構建馬爾可夫鏈的能力,其平穩分布是我們想要采樣的分布。為了做到這一點,Metropolis-Hasting和Gibbs采樣算法都使用了馬爾可夫鏈的一個特殊屬性:可逆性。
????????狀態空間 E 上的馬爾可夫鏈,轉移概率表示為
![]()
????????如果存在概率分布,則稱為可逆γ,使得
![]()
????????對于這樣的馬爾可夫鏈,我們可以很容易地驗證我們有
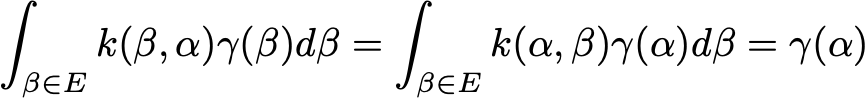
????????然后,γ是一個平穩分布(如果馬爾可夫鏈是不可約的,則是唯一一個)。
????????現在讓我們假設我們想要從中采樣的概率分布π僅定義為一個因子
![]()
????????(其中 C 是未知乘法常數)。我們可以注意到以下等價性成立

????????然后,定義轉移概率 k(.,.) 以驗證最后一個等式的馬爾可夫鏈將如預期的那樣π為平穩分布。因此,我們可以定義一個馬爾可夫鏈,對于平穩分布,有一個無法顯式計算的概率分布π。
3.4 吉布斯采樣過渡 (∞)
????????假設我們要定義的馬爾可夫鏈是 D 維的,使得
![]()
????????吉布斯抽樣方法基于以下假設:即使聯合概率難以處理,也可以計算給定其他維度的單個維度的條件分布。基于這個想法,定義了轉換,以便在迭代 n+1 時,要訪問的下一個狀態由以下過程給出。
????????首先,我們在 X_n 的 D 維度中隨機選擇一個整數 d。然后,我們根據相應的條件概率對該維度進行采樣,假設所有其他維度都保持固定:
![]()
此處

????????是給定所有其他維度的第 d 維的條件分布。
????????正式地,如果我們表示
![]()
????????然后可以寫入轉移概率

因此,對于唯一非平凡的情況,本地余額按預期進行驗證,
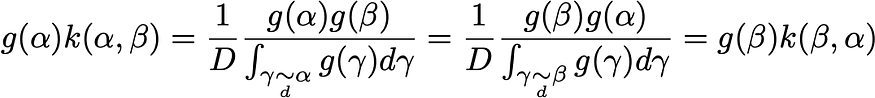
3.5 大都會-黑斯廷過渡(∞)
英文:The Metropolis-Hasting transitions 譯成:大都會-黑斯廷
????????有時,甚至吉布斯方法中涉及的條件分布也太復雜而無法獲得。在這種情況下,可以使用大都會-黑斯廷。為此,我們首先定義一個邊轉移概率 h(.,.) 用于建議轉換。然后,在迭代 n+1 時,馬爾可夫鏈要訪問的下一個狀態由以下過程定義。我們首先從 h 中繪制一個“建議轉換”x,并計算一個相關的概率 r 來接受它:

????????然后選擇有效轉換,以便

從形式上講,可以編寫轉移概率

因此,本地余額按預期驗證

3.6 取樣過程
????????一旦定義了馬爾可夫鏈,我們就可以模擬隨機狀態序列(隨機初始化),并保持其中一些狀態的選擇,例如獲得既遵循目標分布又獨立的樣本。
????????首先,為了使樣本(幾乎)遵循目標分布,我們只需要考慮距離生成序列的開頭足夠遠的狀態,以幾乎達到馬爾可夫鏈的穩態(穩態,理論上,只是漸近到達)。因此,第一個模擬狀態不能用作樣本,我們將達到平穩性所需的階段稱為老化時間。請注意,在實踐中,很難知道此老化時間必須持續多長時間。
????????其次,為了擁有(幾乎)獨立的樣本,我們無法在老化時間之后保留序列的所有連續狀態。事實上,馬爾可夫鏈定義意味著兩個連續狀態之間存在很強的相關性,然后我們需要僅將彼此相距足夠遠的狀態作為樣本,以被視為幾乎獨立。在實踐中,可以通過分析自相關函數(僅適用于數值)來估計兩個狀態之間幾乎獨立的滯后。
????????因此,為了獲得遵循目標分布的獨立樣本,我們保留了生成序列中的狀態,這些狀態由滯后 L 彼此隔開,并且在老化時間 B 之后出現。因此,如果表示馬爾可夫鏈的連續狀態
![]()
????????我們只保留狀態作為我們的樣本
![]()

MCMC采樣需要考慮老化時間和滯后。
四、變分推理(六)
????????克服與推理問題相關的計算困難的另一種可能方法是使用變分推理方法,該方法包括找到參數化族中分布的最佳近似值。為了找到這個最佳近似值,我們遵循一個優化過程(基于族參數),只需要定義目標分布到一個因子。
4.1 近似方法
????????VI方法包括搜索給定族中某些復雜目標概率分布的最佳近似。更具體地說,這個想法是定義一個參數化的分布族,并對參數進行優化,以獲得相對于明確定義的誤差度量最接近目標的元素。
????????我們仍然考慮將概率分布π定義為歸一化因子 C:
![]()
????????然后,用更數學的術語來說,如果我們表示分布的參數族
![]()
????????我們考慮兩個分布 p 和 q 之間的誤差度量 E(p,q),我們搜索最佳參數,使得
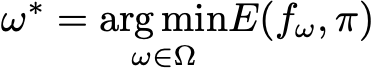
????????如果我們可以在不必顯式歸一化π的情況下解決這個最小化問題,我們可以使用 f_ω* 作為近似值來估計各種量,而不是處理棘手的計算。變分推理方法所隱含的優化問題實際上應該比直接計算(歸一化、組合數學等)的問題更容易處理。
????????與抽樣方法相反,假設一個模型(參數化族),這意味著偏差,但也意味著較低的方差。一般來說,VI方法不如MCMC方法準確,但產生結果的速度要快得多:這些方法更適合大規模,非常統計的問題。

近似方法(變分推理)的圖解。
4.2 分布家族
????????我們需要設置的第一件事是參數化分布族,它定義了我們搜索最佳近似的空間。
????????系列的選擇定義了一個控制方法偏差和復雜性的模型。如果我們假設一個非常嚴格的模型(簡單家族),那么我們就會有很高的偏差,但優化過程很簡單。相反,如果我們假設一個相當自由的模型(復雜家族),偏差要低得多,但優化會更難(如果不是難以處理的話)。因此,我們必須在復雜到足以確保最終近似質量的族和足夠簡單的族之間找到適當的平衡,以使優化過程易于處理。我們應該記住,如果家族中沒有分布接近目標分布,那么即使是最好的近似也會給出糟糕的結果。
????????均場變分族是一系列概率分布,其中所考慮的隨機向量的所有分量都是獨立的。該系列的分布具有產品密度,因此每個獨立組件都由產品的不同因子控制。因此,屬于均場變分族的分布具有可以寫的密度

????????其中我們假設了一個 m 維隨機變量 z。請注意,即使在表示法中省略了它,所有密度f_j都是參數化的。因此,例如,如果每個密度f_j都是具有均值和方差參數的高斯,則全局密度 f 由來自所有獨立因子的一組參數定義,并且對整組參數進行優化。
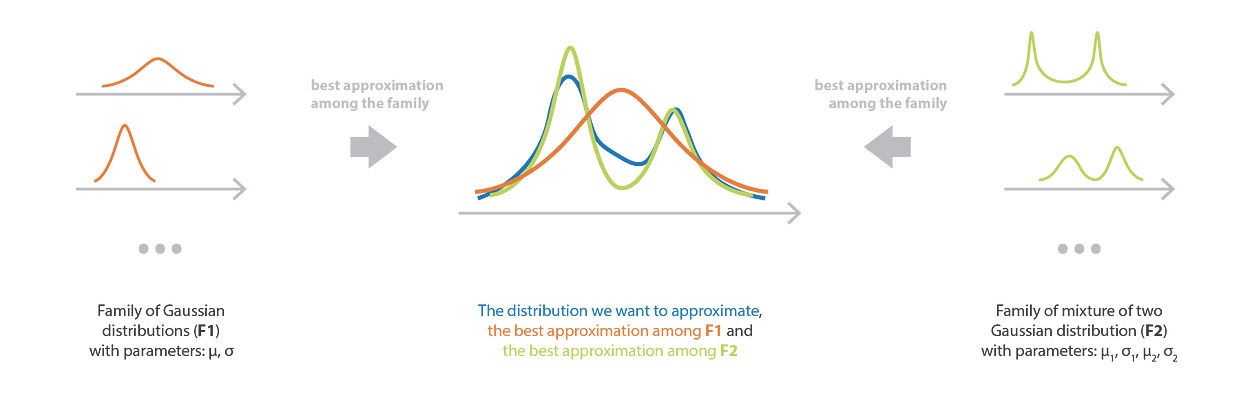
變分推理中族的選擇既決定了優化過程的難度,也決定了最終近似的質量。
4.3 庫爾巴克-萊布勒背離
????????一旦定義了族,一個主要問題仍然存在:如何在這個族中找到給定概率分布的最佳近似值(明確定義為其歸一化因子)?即使最佳近似顯然取決于我們考慮的誤差度量的性質,假設最小化問題不應該對歸一化因子敏感似乎是很自然的,因為我們想比較質量分布而不是質量本身(對于概率分布必須是單一的)。
????????因此,現在讓我們定義Kullback-Leibler(KL)背離,并看到該度量使問題對歸一化因子不敏感。如果 p 和 q 是兩個分布,則 KL 散度定義如下
![]()
????????從這個定義中,我們可以很容易地看到我們有
![]()
????????這意味著我們的最小化問題的以下相等性

????????因此,當選擇KL散度作為我們的誤差度量時,優化過程對乘法系數不敏感,我們可以在參數化分布族中搜索最佳近似值,而不必像預期的那樣計算目標分布的痛苦歸一化因子。
????????最后,作為一個附帶事實,我們可以通過向感興趣的讀者注意KL散度是交叉熵減去熵來結束這一小節,并且在信息論中有一個很好的解釋。
4.4 優化過程和直覺
????????一旦定義了參數化族和誤差度量,我們就可以初始化參數(隨機或根據明確定義的策略)并繼續進行優化。可以使用幾種經典的優化技術,例如梯度下降或坐標下降,在實踐中,這將導致局部最優。
????????為了更好地理解這個優化過程,讓我們舉一個例子,回到貝葉斯推理問題的具體案例,我們假設一個后驗,使得
![]()
????????在這種情況下,如果我們想使用變分推理獲得該后驗的近似值,我們必須求解以下優化過程(假設參數化族定義并將KL散度作為誤差度量)

????????最后一個等式有助于我們更好地理解如何鼓勵近似來分配其質量。第一項是預期對數似然,它傾向于調整參數,以便將近似的質量放在潛在變量 z 的值上,這些值可以最好地解釋觀測數據。第二項是近似和先驗之間的負KL散度,它傾向于調整參數以使近似接近先驗分布。因此,這個目標函數很好地表達了通常的先驗/似然平衡。
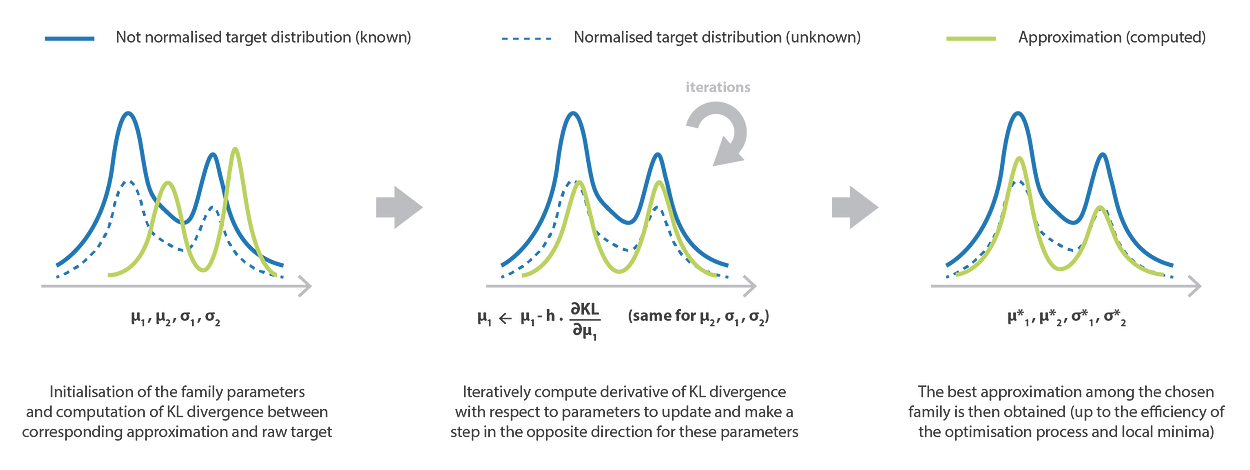
變分推理方法的優化過程。
五、總結
本文的主要內容是:
- 貝葉斯推理是統計學和機器學習中一個非常經典的問題,它依賴于眾所周知的貝葉斯定理,其主要缺點在于大多數時候,在一些非常繁重的計算中。
- 馬爾可夫鏈蒙特卡羅(MCMC)方法旨在模擬密度的樣品,這些密度可能非常復雜和/或定義到一個因子
- MCMC可用于貝葉斯推理,以便直接從后驗的“未歸一化部分”生成要使用的樣本,而不是處理棘手的計算
- 變分推理 (VI) 是一種近似分布的方法,它使用參數優化過程來找到給定族中的最佳近似
- VI優化過程對目標分布中的乘法常數不敏感,因此,該方法可用于近似定義到歸一化因子的后驗
????????如前所述,MCMC和VI方法具有不同的屬性,這意味著不同的典型用例。一方面,MCMC方法的采樣過程非常繁重,但沒有偏差,因此,當預期獲得準確的結果時,這些方法是首選,而不考慮所需的時間。另一方面,盡管VI方法中系列的選擇可能會明顯引入偏差,但它伴隨著合理的優化過程,使這些方法特別適用于需要快速計算的非常大規模的推理問題。
????????MCMC和VI之間的其他比較可以在優秀的變分推理:統計學家評論中找到,我們也強烈推薦給僅對VI感興趣的讀者。有關MCMC的進一步閱讀,我們建議使用此一般介紹以及此面向機器學習的介紹。有興趣了解有關應用于LDA的吉布斯采樣的更多信息的讀者可以參考這個關于主題建模和吉布斯采樣的教程(結合這些關于LDA Gibbs采樣器的講義,以便謹慎推導)。約瑟夫·羅卡
?????







)

入門介紹篇:Maven基礎概念與其他構建工具:理解構建過程與Maven的多重作用,以及與敏捷開發的關系 ~)
——MDI窗口 QMdiArea QMdiSubWindow)




)



