?

目錄

?正態分布

正態分布的參數

正態分布的第一個參數是均值

正態分布的第二個參數是標準差SD

所有正態分布的共同特征

標準正態分布：正態分布的特例

中心極限定理

理解定義

示例# 1

示例# 2

知道樣本均值總是正態分布的實際含義是什么？

---

?正態分布

????????正態分布也被稱為高斯分布或鐘形曲線（因為它看起來像一個鐘），這是統計學中最重要的概率分布，就像我們在大自然中經常看到的那樣，它有點神奇。例如，身高、體重、血壓、測量誤差、智商得分等都服從正態分布。

????????還有一個跟它相關的，并且非常重要的概念，叫中心極限定理，我們后面會提到。

? ? ? ? 由上圖可得一個正常變量的值是如何分布的。這是一個對稱分布，其中大多數觀測值聚集在具有最高發生概率的中心峰（均值/平均值）附近，并且當我們在兩個方向上都偏離中心峰時，我們看到曲線尾部出現值的可能性越來越小。此圖描繪了一個群體的智商水平，可以理解，智商水平非常低或智商水平很高的人很少見，并且大多數人都處于平均智商得分范圍內。?

正態分布的參數

????????正態分布總是以平均值為中心，而曲線的寬度則由標準差(SD)決定。

????????這是兩個正態分布，x軸上的高度單位是英寸，y軸上是特定高度對應的人數。

????????1. 嬰兒的平均身高為20英寸（50cm），標準差為0.6英寸（1.5cm）

????????2. 成年人的平均分布為70英寸（175cm），標準差為4英寸（10cm）

????????了解正態分布標準差的意義在于，它遵循一個經驗法則，即大約95%的測量值落在均值附近的+/- 2倍個標準差之間。

????????推論：95%的人口落在平均值+/- 2*SD之間

????????1. 95%的嬰兒身高在20 +/- 1.2英寸之間

????????2. 95%的成年人身高測量值在70 +/- 8英寸之間

正態分布的第一個參數是均值

????????均值或平均值是正態分布的集中趨勢，它決定了曲線峰值的位置。平均值的變化導致曲線沿x軸水平移動。

正態分布的第二個參數是標準差SD

????????標準差是正態分布變異性的量度，它決定了曲線的寬度。SD值的變化導致曲線變得更窄或更寬，并對曲線的高度產生反比例的影響。

????????更緊的曲線(較小的寬度)->更高的高度

????????更寬的曲線(更高的寬度)->更短的高度

????????現在，你已經了解了正態分布曲線的所有基礎知識。讓我們繼續學習與之相關的其他重要信息。

所有正態分布的共同特征

????????1. 它們都是對稱的

????????2. 平均值=中位數

? ? ? ? 3. 根據經驗法則，我們可以確定正態分布曲線離均值標準差范圍內的數據百分比。

????????通過一個示例，這一點將變得更加清楚。

????????讓我們來看一個披薩外賣的例子。假設一家披薩餐廳的平均配送時間為30分鐘，標準偏差為5分鐘。根據經驗法則，我們可以確定68%的交付時間在25-35分鐘(30 +/- 5)之間，95%在20-40分鐘(30 +/- 2*5)之間，99.7%在15-45分鐘(30 +/-3*5)之間。

標準正態分布：正態分布的特例

????????如前所述，正態分布根據參數值(平均值和標準差)有許多不同的形狀。標準正態分布是正態分布的一個特例，均值為0，標準差為1。這個分布也稱為Z分布。標準正態分布上的值稱為標準分數或Z分數。標準分數表示某一特定觀測值高于或低于平均值的SD數。

????????例如，標準得分為1.5表示觀察到的結果比平均值高1.5個標準差。另一方面，負分數表示低于平均值的值。平均值的Z分數為0。

---

中心極限定理

?????????中心極限定理（CLT）指出，如果樣本量足夠大，則變量均值的采樣分布將近似于正態分布，而與該變量在總體中的分布無關。

理解定義

示例# 1

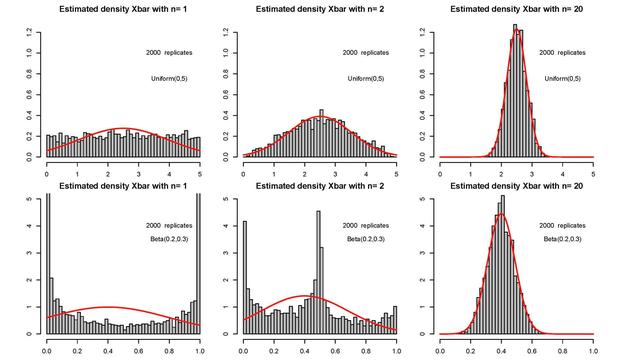
????????選取一個均勻分布[0,1]，它被稱為均勻分布，因為在0和1之間選擇值的概率相等，因此它的概率密度函數(PDF)是水平的直線。現在，讓我們假設我們從這個分布中隨機抽取20個樣本(綠點)并計算這些樣本的均值，我們得到一個值，在這個例子中是0.5，用虛線表示。讓我們把這個平均值畫在直方圖上。由于這個柱狀圖到目前為止只有一個平均值，它并沒有告訴我們任何其他信息（左圖）。繼續從相同的分布中提取更多的隨機樣本，計算各自的平均值并將這些平均值繪制在直方圖上，我們開始得到一個有趣的結果。

????????隨著我們從均勻分布中抽取越來越多的隨機樣本，并在直方圖上繪制樣本均值，我們得到一個正態分布結果如下(見右曲線)。

推論：我們從均勻的數據分布開始，但是從中抽取的樣本均值是正態分布。

示例# 2

????????在第二個例子中，讓我們按照與第一個例子相同的步驟，唯一的不同是我們這次要從指數分布中提取樣本。

????????我們將再次隨機抽取20個樣本，計算樣本的均值，并將其繪制在直方圖上。計算100這樣的樣本的均值并將其畫在直方圖上，這樣的分布對我們來說并不陌生。樣本均值是正態分布！

推論：我們從指數數據分布開始，但從中抽取樣本的均值得到正態分布。

????????我們從指數數據分布開始，但是從中抽取的樣本均值得到正態分布。因此，它在這一點上變得非常直觀，中心極限定理意味著什么？

? ? ? ? 中心極限定理意味著即使數據分布不是正態的，從中抽取的樣本均值的分布也是正態的。

知道樣本均值總是正態分布的實際含義是什么？

????????在分析領域，我們每天都會遇到各種各樣的數據，而源數據的分布并不總是被我們所知道的，但是，因為我們了解中心極限定理，所以我們甚至不需要關心源數據的分布，因為我們總是可以得到正態分布。

????????為了使中心極限定理能夠起作用，我們必須能夠計算出樣本的平均值。有一個分布稱為柯西分布，沒有樣本均值，從而中心極限定理論并不適用于它，但除了柯西分布，我沒有遇到除中心極限定理以外的任何其他分布。)

下面是了解均值正態分布的實際含義：

1. 我們可以用均值的正態分布來分配置信區間。

2. 我們可以進行T檢驗（即兩個樣本均值之間是否存在差異）

3. 我們可以進行方差分析（即3個或更多樣本的均值之間是否存在差異）