Problem: 283. 移動零

思路

首先我們來講一下本題的思路

• 本題主要可以歸到【數組劃分/數組分塊】這一類的題型。我們將一個數組中的所有元素劃分為兩段區間，左側是非零元素，右側是零元素

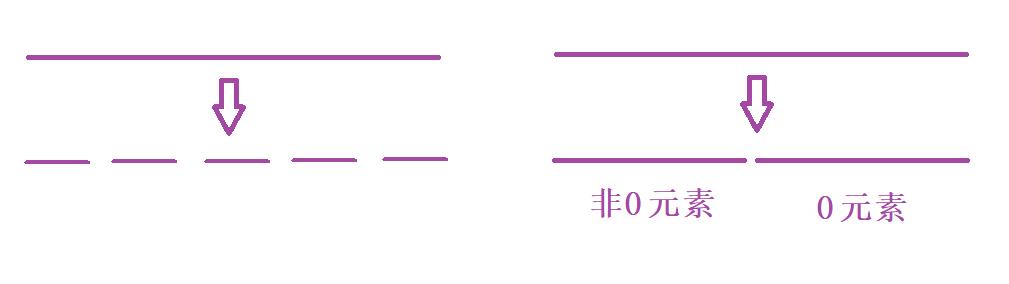
• 那解決這一類的題我們首先想到的就是【雙指針算法】，學習過C語言的同學應該就可以知道指針是比較繁瑣和復雜，如果有興趣學習的同學可以看看我的這篇文章 鏈接
• 不過在這里呢我們不需要去使用int*這種指針，而是直接使用數組下標來充當指針即可

好，那我們就來看看這個雙指針到底是怎樣的，要如何去使用

• 兩個指針的作用
  • 【cur】： 從左往右掃描數組，遍歷數組
  • 【dest】：已處理的區間內，非零元素的最后一個位置
• 可以看到，cur是我們用來遍歷數組的，從[cur, n - 1]就是還未處理的元素；那么從[0, cur]就是已經處理過的元素，但是呢本題的要求是我們要劃分出【零元素】與【非零元素】，所以呢前面的區間我們可以再度劃分為[0, dest]和[dest + 1, cur - 1]

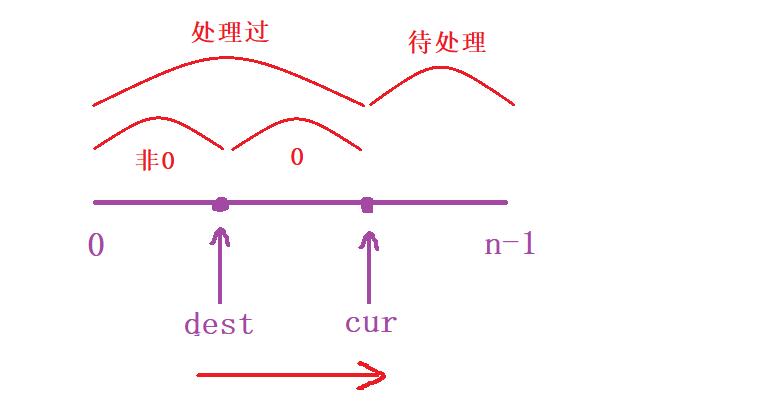
小結一下：

[0, dest] [dest + 1, cur - 1] [cur, n - 1]

• [0, dest] —— 非零元素
• [dest + 1, cur - 1] —— 零元素
• [cur, n - 1] —— 未處理元素

算法圖解分析

接下去我們就通過畫算法圖解的形式來模擬一下解題的過程

• 我們就以題目中所給出的第一個示例為例來進行講解，因為在一開始我們還沒處理過任何的非零元素，所以對于[0, cur - 1]這段區間是沒有任何數據的，所以在一開始我們可以將【dest】這個指針置于-1的位置

• 因為我們需要將非0元素移動到前面，所以呢如果遇到了0元素的話，cur++即可，將其留在這個位置上

• 那當我們遇到非0元素時，就需要將其交換到前面去，那我們[0, dest]這個區間就是用來存放非0元素的，此時多了一個元素的話那dest就要加1，原本其是指向-1這個位置，那我們可以使用++dest來完成

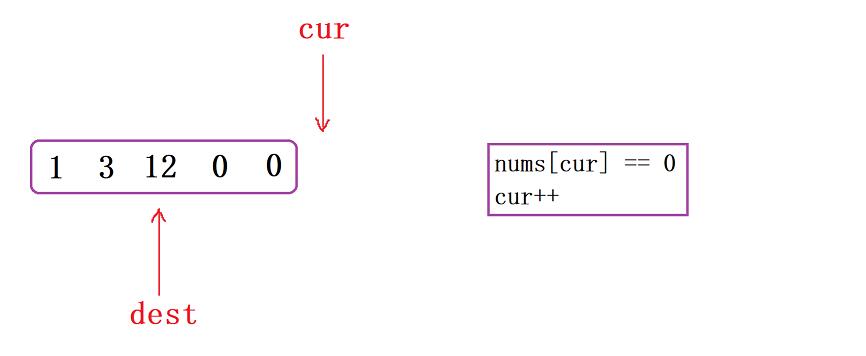
• 接下去，當數據交換過來后，我們可以去對照上面的這三個區間，可以發現最左側是非0元素，中間是0元素，右側呢則是待處理的元素。接下去我們又碰到了0元素，所以cur++

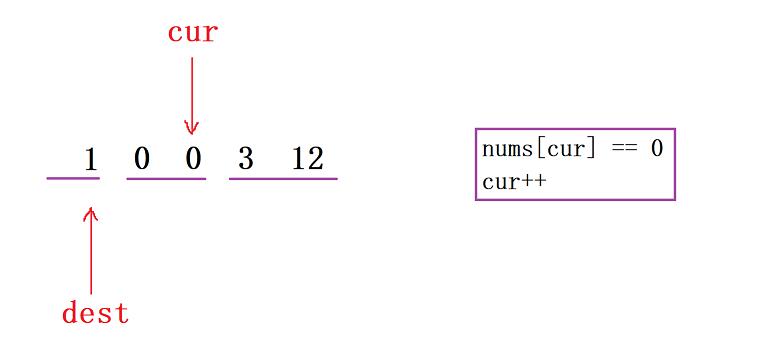
• cur再后移之后呢，我們又碰到了非0元素，繼續讓dest上來然后交換二者位置上的元素

• 那現在我們再來看這三個區間，左側還是保持為【非0元素】，中間為【0元素】，右側的話則是【待處理的元素】

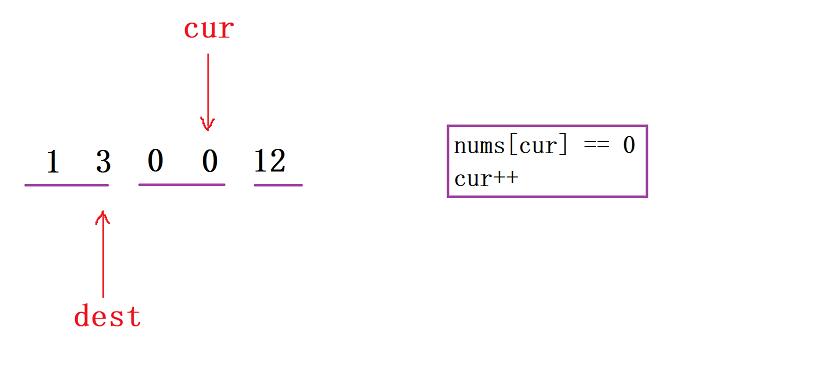
• 然后碰到非0元素后，繼續讓++dest，然后做交換

• 最后的話我們來看看這個處理完后的整個區間元素：非0元素都在前面，而0元素則都在后面，[cur, n - 1]的這段區間也不存在了，說明已經沒有待處理元素了

復雜度

接下去我們來分析一下本題的時空復雜度

• 時間復雜度:

本算法的核心思路參考的是【快速排序】的區間劃分，我們這里就是在不斷遍歷數組的過程中，以中間的0作為分割，然后左側是非0元素，右側是未處理的元素。在處理的過程中我們只是遍歷了一次這個數組，所以復雜度為 $O(n)$

• 空間復雜度:

在本題中我們并沒有去開出額外的空間，所以復雜度為 $O(1)$

Code

class Solution {
public:void moveZeroes(vector<int>& nums) {for(int dest = -1, cur = 0; cur < nums.size(); ++cur){if(nums[cur] != 0){swap(nums[++dest], nums[cur]);}}}
};