????????在 Simulink? 模型中,當存在信號環并且信號環中只存在直接饋通模塊時,將出現代數環。直接饋通表示 Simulink 需要模塊輸入信號的值來計算當前時間步的輸出。這種信號循環會在同一時間步中產生模塊輸出和輸入的循環依存關系。這會導致一個需要在每個時間步求解的代數方程,從而增加仿真的計算成本。
下面是具有直接饋通輸入的模塊的一些示例:
·Math Function
·Gain
·Product
·State-Space,當 D 矩陣系數為非零時
·Sum
·Transfer Fcn,當分子和分母同階時
·Zero-Pole,當模塊的零值與極點一樣多時
非直接饋通模塊維護一個 State 變量。其中兩個示例是 Integrator 和 Unit Delay 模塊。
提示
????????要確定一個模塊是否具有直接饋通,請閱讀模塊參考頁的特性部分。
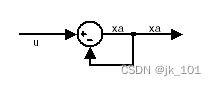
????????下圖顯示代數環的一個示例。Sum?模塊是一個代數變量 xa,該變量必須等于第一個輸入 u 減去 xa(例如?xa?= u – xa)。

?此簡單循環的解為?xa?= u/2。
數學解釋
????????Simulink 包含一套用于對常微分方程 (ODE)?進行仿真的數值求解器,它們是您可以寫為以下形式的方程組:
![]()
其中 x 是狀態向量,t 是時間自變量。???????
?????????某些方程組包含涉及自變量和狀態向量,但不涉及狀態向量的導數的其他約束。此類方程組稱為微分代數方程 (DAE)。
????????代數一詞是指不涉及任何導數的方程。您可以用半顯式格式來表示工程中出現的 DAE

其中:
-
f?和?g?可以是向量函數。
-
第一個方程是微分方程。
-
第二個方程是代數方程。
-
微分變量的向量是?x。
-
代數變量的向量是?xa。
????????在 Simulink 模型中,代數環是代數約束。具有代數環的模型定義微分代數方程組。在 ODE 求解器的每個步長中,Simulink 以數值方式求解代數方程(代數環)的 xa。
圖窗中的模型等同于此方程組的半顯式形式:


在 ODE 求解器的每個步長中,代數環求解器必須先求解代數約束的 xa,然后再計算導數?˙x。
物理解釋
代數約束:
-
在對物理系統建模時發生,通常是守恒定律所致,例如質量與能量守恒
-
當您為模型選擇特定坐標系時發生
-
對動態系統中的系統響應的設計進行約束
????????使用 Simscape? 將跨越機械、電氣、液壓和其他物理領域的系統建模為物理網絡。Simscape 構造描述模型行為的 DAE。軟件將這些方程與模型的其余部分集成,然后直接解算 DAE。Simulink 同時對不同物理領域中的組件變量求解,從而避免代數環問題。
人為代數環
????????當原子子系統或 Model 模塊導致 Simulink 檢測到代數環時,將發生人為代數環,即使該子系統的內容不包含從輸入到輸出的直接饋通也是如此。當您創建原子子系統時,所有 Inport 模塊都將是直接饋通,從而導致代數環。
????????以包含的模型為例,該模型表示被控對象的簡單比例控制,其描述如下

它可以重寫為以下狀態空間形式:?
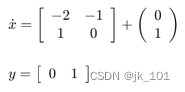
該方程組既沒有代數變量也沒有直接饋通,因此不包含代數環。
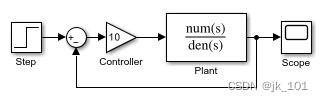
?按照以下步驟中的說明修改模型:
-
將 Controller 和 Plant 模塊包含在子系統中。
-
在子系統對話框中,選擇視為原子單元使子系統成為原子子系統。
-
在模型配置參數的診斷窗格中,將代數環參數設置為?
error。

????????在對此模型進行仿真時,會出現代數環,因為該子系統是直接饋通,即使原子子系統內的路徑不是直接饋通也是如此。仿真停止并出現代數環錯誤。
代數環求解器的工作原理
????????當模型中包含代數環時,Simulink 在每個時間步使用非線性求解器解算代數環。求解器執行迭代以確定代數約束的解(如果存在)。因此,有代數環的模型的運行速度可能比沒有代數環的模型的運行速度慢。
????????Simulink 使用折線信賴域算法解算代數環。使用的容差小于 ODE 求解器?Reltol?和?Abstol。這是因為 Simulink 使用“顯式 ODE 方法”來解算指數為 1 的微分代數方程 (DAE)。
要使代數環求解器發揮作用,
-
必須存在一個模塊,在該模塊中,代數環求解器可以中斷循環并嘗試解算該循環。
-
模型應該具有雙精度實信號。
-
基礎代數約束必須是一個平滑函數。
????????例如,假設您的模型中有一個帶兩個輸入的 Sum 模塊:一個相加,另一個相減。如果您將 Sum 模塊的輸出饋送給其中一個輸入,則會創建一個代數環,其中的所有模塊都包括直接饋通。
????????Sum 模塊無法在不知道輸入的情況下計算輸出。Simulink 會檢測代數環,代數環求解器將使用迭代循環解算代數環。在 Sum 模塊示例中,該軟件通過以下方式計算正確的結果:
| xa(t) = u(t) /2. | (1) |
????????代數環求解器使用基于梯度的搜索方法,這需要與代數環相對應的代數約束的連續一階導數。因此,如果代數環包含不連續性,代數環求解器可能會失敗。
代數環求解器中的信賴域算法和行搜索算法
????????Simulink 代數環求解器使用下面兩種算法之一來解算代數環:
-
信賴域
-
行搜索
????????默認情況下,Simulink 選擇最佳代數環求解器,并可能在仿真期間在兩種方法之間切換。要為模型顯式啟用自動代數環求解器選項,請在 MATLAB??命令行中輸入:
set_param(model_name, 'AlgebraicLoopSolver','Auto');????????要切換到信賴域算法,請在 MATLAB 命令行中,輸入:
set_param(model_name, 'AlgebraicLoopSolver', 'TrustRegion');????????如果代數環求解器不能解算使用信賴域算法的代數環,請嘗試使用行搜索算法對模型進行仿真。
要切換到行搜索算法,請在 MATLAB 命令行中,輸入:
set_param(model_name, 'AlgebraicLoopSolver', 'LineSearch');代數環求解器的限制
????????代數環解算是一個迭代過程。僅當代數環收斂到一個明確的答案時,Simulink 代數環求解器才會成功。當代數環無法收斂,或收斂速度太慢時,仿真將退出并顯示錯誤。
????????代數環求解器無法解算包含以下任何一項的代數環:
-
帶有離散值輸出的模塊
-
帶有非雙精度或復數輸出的模塊
-
不連續點
-
Stateflow??圖
模型中代數環的影響
如果模型包含代數環:
-
不能為模型生成代碼。
-
Simulink 代數環求解器可能無法解算代數環。
-
由于 Simulink 會嘗試解算代數環,因此仿真執行速度可能很緩慢。
對于大多數模型,代數環求解器的第一個時間步會耗費大量計算資源。Simulink 能夠快速解算后續時間步,因為上一個時間步為 xa?提供了良好的起點。













)





