專注 效率 記憶
預習 筆記 復習 做題
歡迎觀看我的博客,如有問題交流,歡迎評論區留言,一定盡快回復!(大家可以去看我的專欄,是所有文章的目錄)
文章字體風格:
紅色文字表示:重難點★?
藍色文字表示:思路以及想法★?
如果大家覺得有幫助的話,感謝大家幫忙
點贊!收藏!轉發!
本博客帶大家一起學習,我們不圖快,只求穩扎穩打。
由于我高三是在家自學的,經驗教訓告訴我,學習一定要長期積累,并且復習,所以我推出此系列。
只求每天堅持40分鐘,一周學5天,復習2天
80天后我們學習完《深入理解計算機系統》
本課程來自b站 九曲闌干
【80天學習完《深入理解計算機系統》】第三天 2.3 整數運算
- 1. 255+1 = 0
- 2. 如何判斷溢出
- 3. 逆元
- 4. 補碼加法 正負溢出
- 兩個正數相加 小于 0 正溢出
- 兩個負數相加 大于0 負溢出
- 正溢出
- 負溢出
- 5. 乘法和位運算
- C語言類型轉換
- -x = (~x)+ 1
- 1. 二進制表示浮點數
- V = (-1)^s^ × M × 2 ^E^
- 非規格數(M = 1 + f)規格化(M = f )
- E = e - bias
- bias = 2^8-1^-1
- 2. 非規格化的數的作用
- 浮點數的0
- 表示接近0的數
- 3. 特殊值
- 4. 類比于1字節表示 浮點數
- 5. 12345 和 12345.0 的二進制對比
- 6. 浮點數舍入
- 向上向下舍入 就畫數軸
- 向偶數舍入 比如 1.5
- 7. 浮點數 加減乘除法可能不適合 結合律
- 8. 類型轉換
- 小到大 不會溢出 可能會 舍入
- 大到小 可能溢出 或者 精度降低
- 向0舍入
- 1. int 轉成 float(由于float的有效位是23位)
- 2. 返回補碼最小值
- 3. -x = ~x + 1
- 為什么?
- x + (~x)= -1
- 全是1的二進制 值是-1
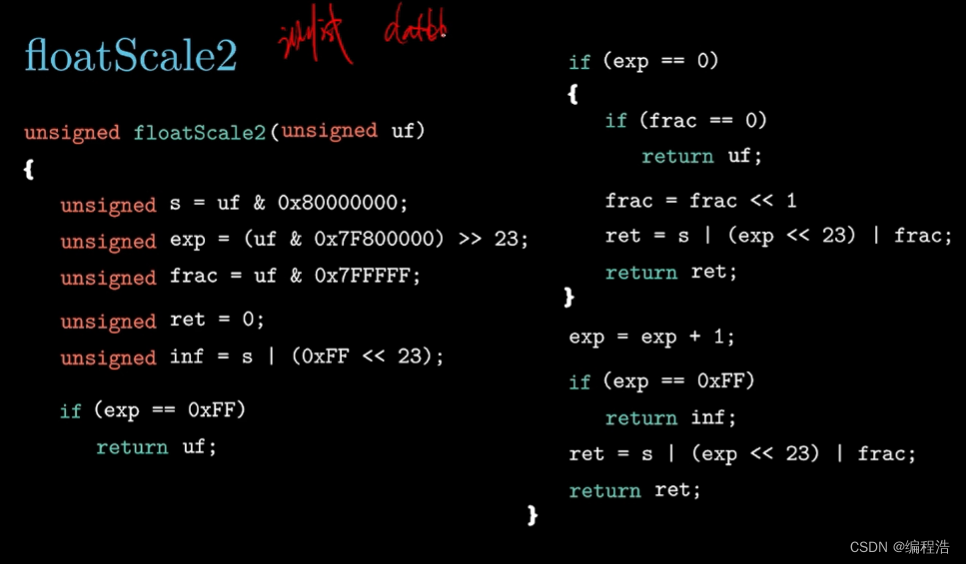
- 4. 無符號int 看成 float 然后返回*2的值
- 1. 先取到exp的值(判斷是否為規格化的數)
- 2. 取frac(與exp一起判斷是否為特殊值)
- 規格化的數:exp !=0 !=255
- 無窮大 exp = 255 并且frac = 0
- 不是一個數 exp = 255 并且 frac !=0
- 非規格化 exp = 0 f = 0 表示 0或者-0(看s)
- 非規格化 exp = 0 f !=0 表示非常接近0
- 答案:
- 1. 返回原數(0值 無窮大值 非數值)
- 2. 無限接近0的數 返回 M*2的值(因為E是為0)
- 3. 返回E*2的值(規格化)
- 4. 如果溢出 則返回特殊值
- 最終答案
- 5. int 和 float哪一個表示的范圍大
- 6. 0.2的浮點數(無限循環小數)

1. 255+1 = 0



2. 如何判斷溢出

3. 逆元

4. 補碼加法 正負溢出
兩個正數相加 小于 0 正溢出
兩個負數相加 大于0 負溢出


正溢出
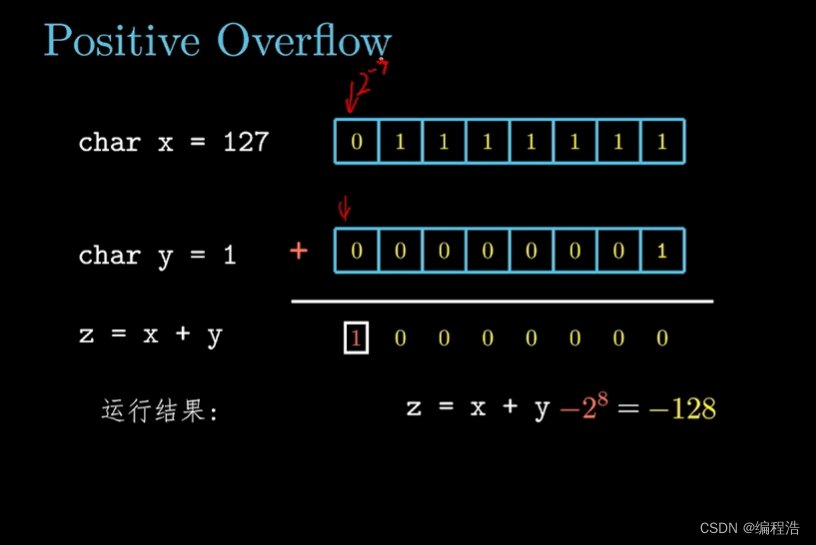
負溢出
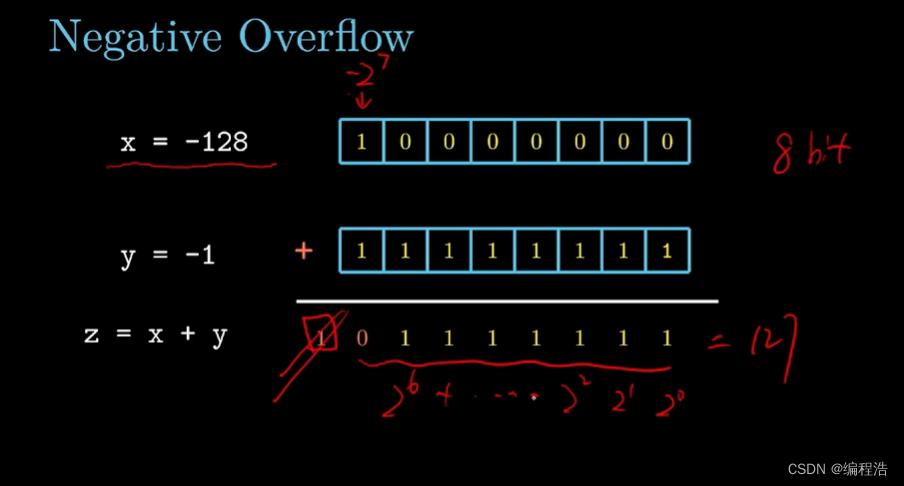
5. 乘法和位運算

C語言類型轉換

-x = (~x)+ 1


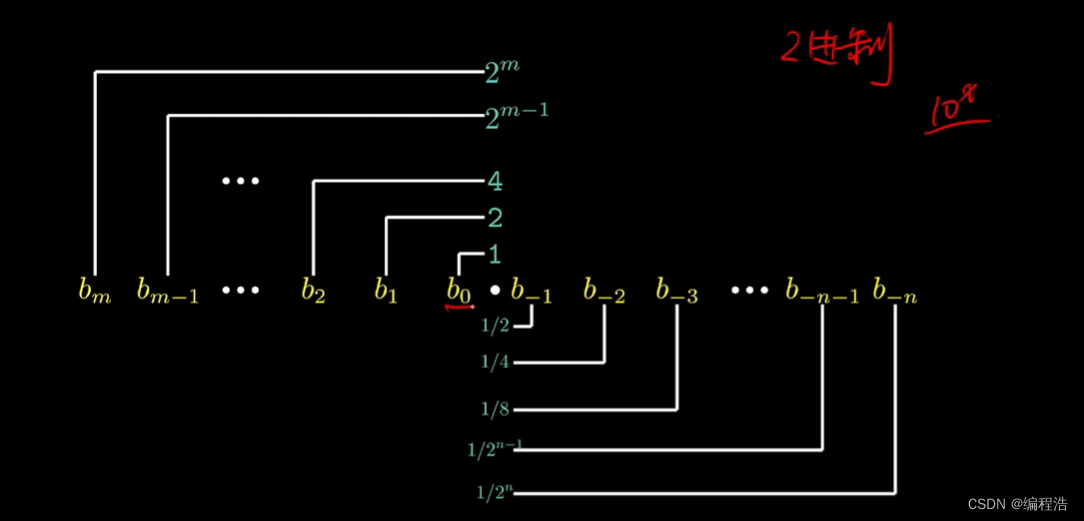
1. 二進制表示浮點數
V = (-1)s × M × 2 E
非規格數(M = 1 + f)規格化(M = f )
E = e - bias
bias = 28-1-1




2. 非規格化的數的作用
浮點數的0
表示接近0的數

3. 特殊值

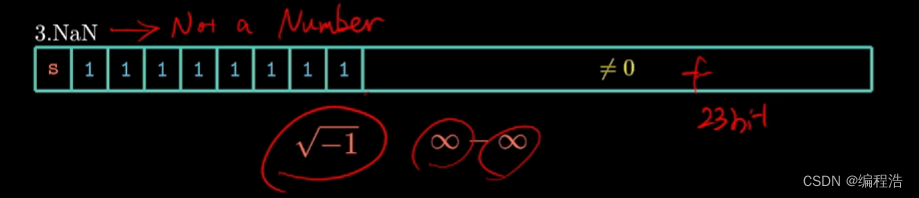
4. 類比于1字節表示 浮點數

5. 12345 和 12345.0 的二進制對比


6. 浮點數舍入
向上向下舍入 就畫數軸
向偶數舍入 比如 1.5
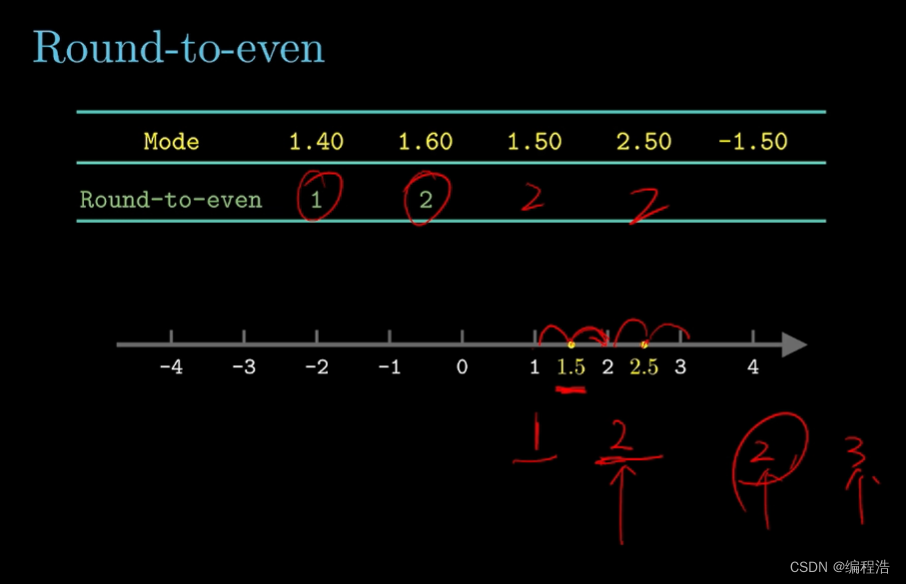
7. 浮點數 加減乘除法可能不適合 結合律


8. 類型轉換
小到大 不會溢出 可能會 舍入

大到小 可能溢出 或者 精度降低

向0舍入

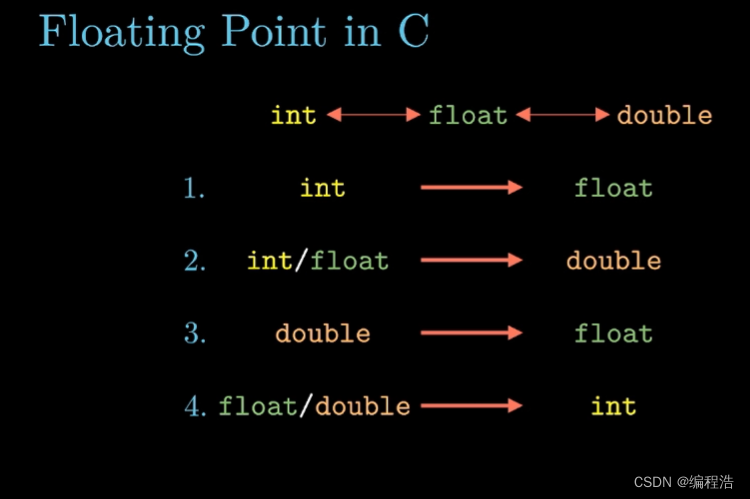
1. int 轉成 float(由于float的有效位是23位)

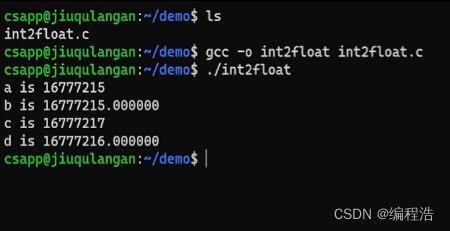

2. 返回補碼最小值
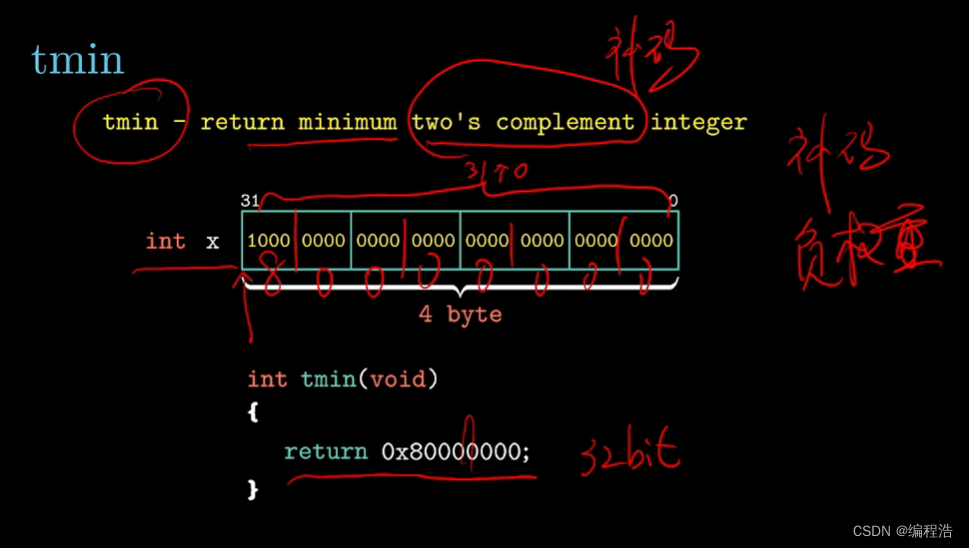
要求 常數不超過8bit

3. -x = ~x + 1
為什么?
x + (~x)= -1
全是1的二進制 值是-1

4. 無符號int 看成 float 然后返回*2的值
1. 先取到exp的值(判斷是否為規格化的數)

2. 取frac(與exp一起判斷是否為特殊值)

規格化的數:exp !=0 !=255
無窮大 exp = 255 并且frac = 0
不是一個數 exp = 255 并且 frac !=0
非規格化 exp = 0 f = 0 表示 0或者-0(看s)
非規格化 exp = 0 f !=0 表示非常接近0

答案:
1. 返回原數(0值 無窮大值 非數值)


2. 無限接近0的數 返回 M*2的值(因為E是為0)

3. 返回E*2的值(規格化)


4. 如果溢出 則返回特殊值

最終答案
5. int 和 float哪一個表示的范圍大

6. 0.2的浮點數(無限循環小數)


)







![[centos]設置主機名](http://pic.xiahunao.cn/[centos]設置主機名)

![[python] 使用Jieba工具中文分詞及文本聚類概念](http://pic.xiahunao.cn/[python] 使用Jieba工具中文分詞及文本聚類概念)








