
1.人工智能框架
機器學習的三要素:模型、學習策略、優化算法。
當我們用機器學習來解決一些模式識別任務時,一般的流程包含以下幾個步驟:
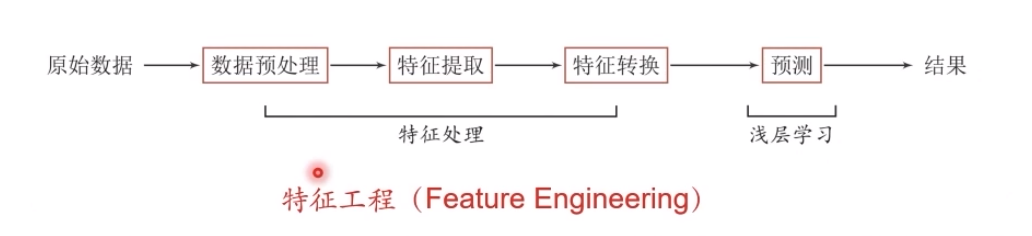
1.1.淺層學習和深度學習
淺層學習(Shallow Learning):不涉及特征學習,其特征主要靠人工經驗或特征轉換方法來抽取。
底層特征VS高層語義:人們對文本、圖像的理解無法從字符串或者圖像的底層特征直接獲得
深度學習通過構建具有一定“深度”的模型,可以讓模型來自動學習好的特征表示(從底層特征,到中層特征,再到高層特征),從而最終提升預測或識別的準確性。

深度學習的數學描述:
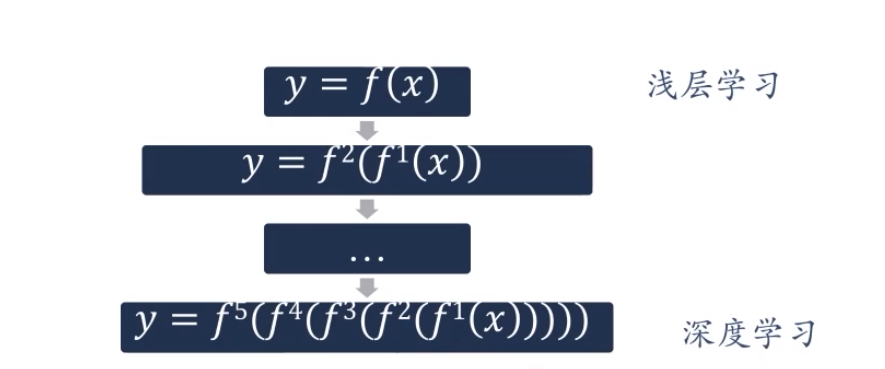
fl(x)為非線性函數,不一定連續。
深度學習的難點:
y=f^5^(f^4^(f^3^(f^2^(f^1^(x)))))
貢獻度分配問題:一個復雜系統中每個組件對最終評價的貢獻。
如何解決貢獻度分配問題:
其中我們一般采用的方法就是求偏導數,也就是使用誤差反向傳播算法,這是我們學習神經網絡的時候接觸到過的。
貢獻度:
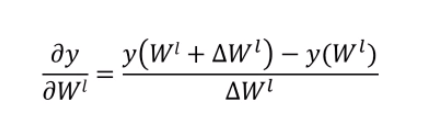
我們要知道一點,那就是神經網絡天然不是深度學習,但深度學習天然是神經網絡!
1.2.神經網絡與深度學習的關系
人工智能的一個子領域
神經網絡:一種以(人工)神經元為基本單元的模型
深度學習:一類機器學習問題,主要解決貢獻度分配問題

我們都明白,機器(深度)學習非常有可能成為計算機學科的關鍵技術。
機器學習必然會發展到深度學習,不一定是神經網絡,基于不可微架構的深度學習可能是未來方向。對于計算機學科是如此,而對于其他學科也是聯系十分的緊密,深度學習也越來越多地成為傳統學科的關鍵技術,涉及到數學、物理、化學、醫藥、天文、地理。
經過兩周騰訊比賽,我對深度學習和強化學習有了自己的感悟:
-
理論支撐不足
-
調參一頭霧水
-
模型無法解釋
-
改進沒有方向
當然,也有玩笑的成分在里面,也算是我和人工智能的第一次接觸下來的感慨吧,領域多、知識點多,理論和實踐緊密結合。
面對這些問題我們該怎么做嘞?
沒錯,就是肝各種前置知識,當然并行一起也可以。數學方面,就是線性代數、微積分、變分法、概率論、優化以及信息論。
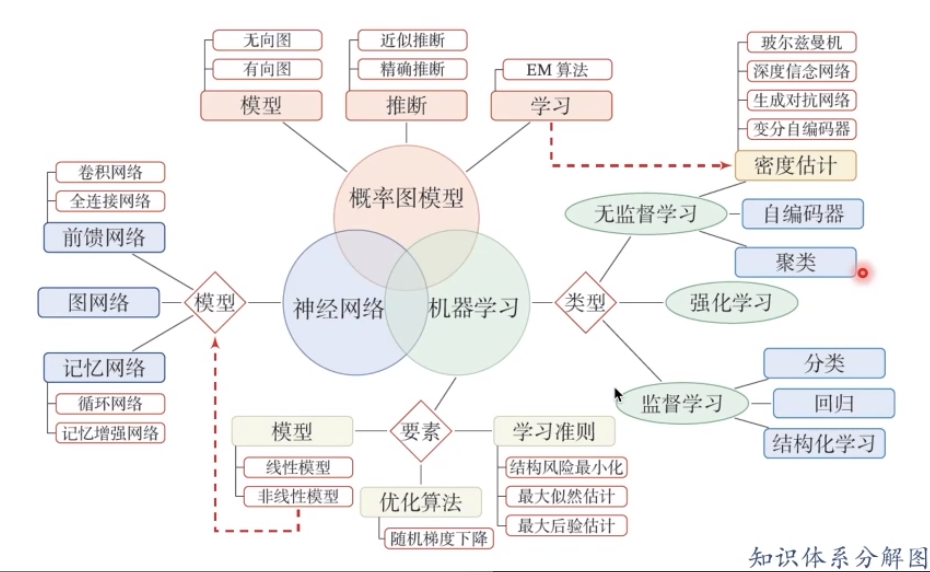
我們需要在學習中逐步形成下面這張圖的知識體系:
機器學習實踐流程中的五要素:
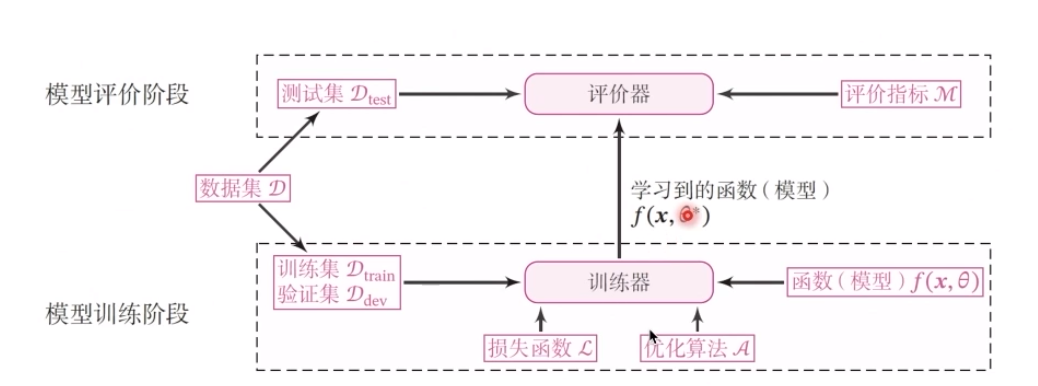
1.3.Runner類
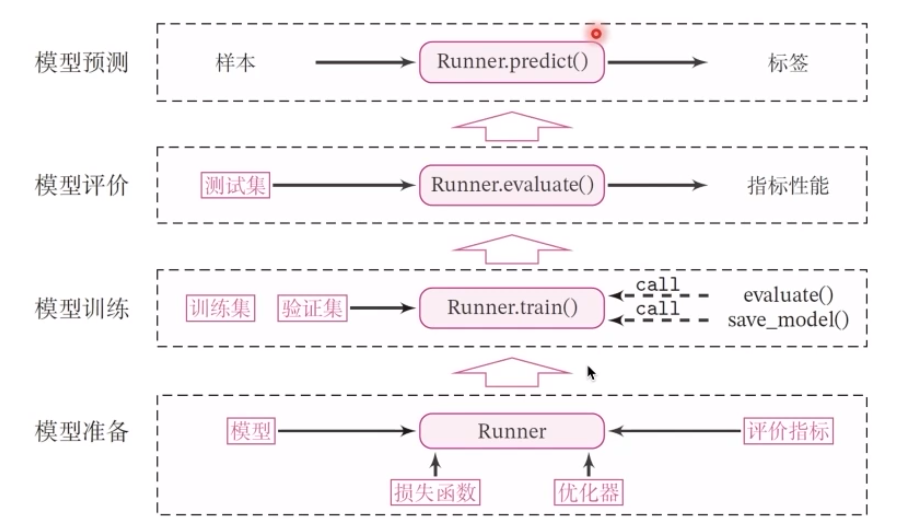
看到圖上的箭頭了嗎,我們在模型準備中就是通過相應的損失函數、評價指標之后,也就是runner運行以后確定了模型合規,然后送到訓練中,可能是強化訓練進行探索,也可能是別的東西。像我們在騰訊開悟的比賽中,就是這樣的形式,訓練一定的時間就會出相應的模型,再提交到指定的平臺進行模型評價和測試評估。
代碼模板:
class Runner(object):def __init__(self, model, optimizer, loss_fn, metric):self.model = model #模型self.optimizer = optimizer #優化器self.1oss_fn = 1oss_fn #損失函數self.metric = metric #評價指標# 模型訓練def train(self, train_dataset, dev_dataset=None, **kwargs):pass# 模型評價def evaluate(self, data_set, **kwargs):pass# 模型預測def predict(self, x, **kwargs):pass# 模型保存def save_model(self, save_path):pass# 模型加載def load_model(self, model_path):pass1.4.張量與算子
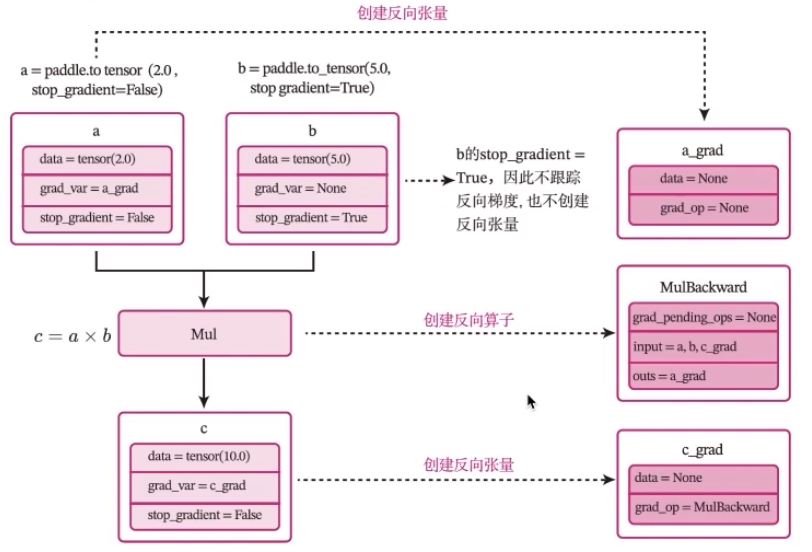
數據的表現形式是張量
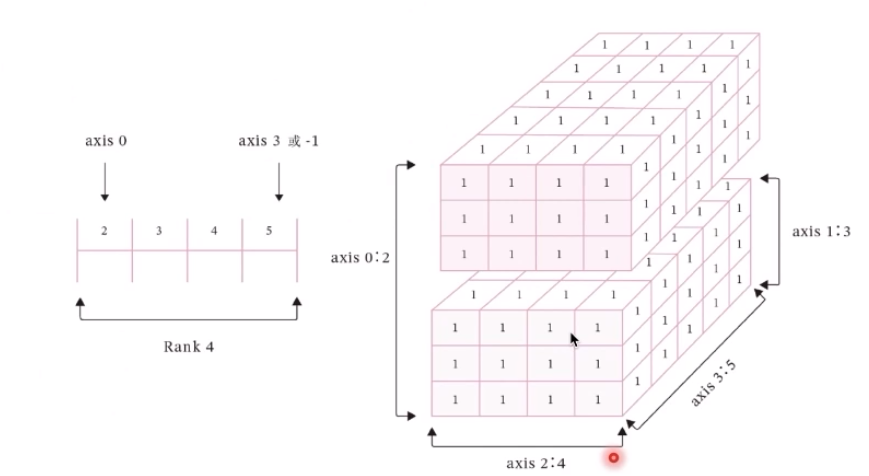
模型的基本單位:算子
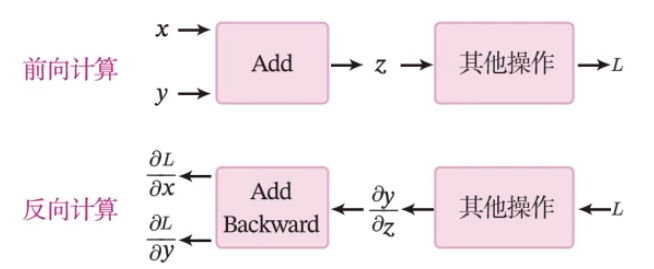
class Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 前向函數# 輸入:張量inputs# 輸出:張量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 反向函數# 輸入:最終輸出對outputs的梯度outputs_grads# 輸出:最終輸出對inputs的梯度inputs_gradsdef backward(self,outputs_grads):# return inputs_gradsraise NotImplementedError加法算子的前向和反向計算過程
一個復雜的機器學習模型(比如神經網絡)可以看做一個復合函數
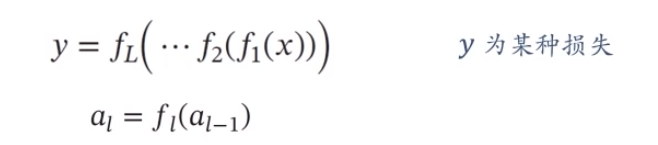
參數學習:梯度計算
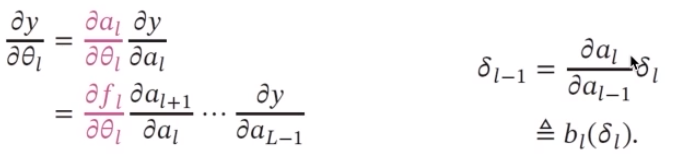
為了繼承飛槳的paddle.nn.layer類
蒲公英一書中實現的Runner類:
RunnerV1
用于線性回歸模型的訓練,其中訓練過程通過直接求解析解的方式得到模型參數,沒有模型優化及計算損失函數過程,模型訓練結束后保存模型參數
Runner V2
主要增加的功能為:①在訓練過程中引入梯度下降法進行模型優化.
②在模型訓練過程中計算訓練集和驗證集上的損失及評價指標并打印,在訓練過程中保存最優模型
Runner V3
主要增加三個功能:使用隨機梯度下降法進行參數優化.訓練過程使用DataLoader加載批量數據.模型加載與保存中,模型參數使用state_dict方法獲取,使用state_dist加載
Runner V3基本上可以應用于大多數機器學習任務。
算子庫nndl
從模型構建角度出發,借鑒深度學習框架中算子的概念,從基礎開始一步步實現自定義的基本算子庫,進一步通過組合自定義算子來搭建機器學習模型,最終搭建自己的機器學習模型庫nndl。
在實踐過程中不僅知其然還知其所以然,更好地掌握深度學習的模型和算法,并理解深度學習框架的實現原理。
2.NNDL開源庫
NNDL (Neural Network Distillation Library) 是一個用于深度學習研究的開源庫,主要用于知識蒸餾(Knowledge Distillation)任務。
知識蒸餾是一種將大型預訓練模型(教師模型)的知識轉移到小型模型(學生模型)的方法。NNDL 提供了一個框架,支持使用圖像分類任務進行知識蒸餾,包括模型定義、訓練和測試等過程。
該庫主要特點包括:
-
支持多種流行的深度學習框架,如 TensorFlow 和 PyTorch。
-
提供多個預訓練的教師模型,以及學生模型的蒸餾訓練。
-
針對圖像分類任務,支持各種數據增強和網絡結構。
-
可用于開發高效的神經網絡模型,包括卷積神經網絡、循環神經網絡等。
請注意,NNDL 是一個相對較新的開源庫,可能存在一些限制和缺陷。在使用過程中,請確保您理解其工作原理和適用范圍,并根據需要進行適當的調整和優化。
NNDL案例與實踐的特色在于:
-
深入理論內部的實踐,比如:從0實現反向傳播、卷積、transformer等。
-
關鍵理論原理的實踐,比如:SRN的記憶能力與梯度爆炸、LSTM的記憶能力等。
-
貼近產業場景的實踐,比如:cnn實現圖像分類、mn實現文本分類、transformer實現語義匹配等。
-
貼近產業工程的實踐,比如:基于訓練框架Runnert的實驗、逐步完善的nnd工具包、模型精度速度的分析方法等。
-
兼顧理論與實踐的作業設計,比如:基礎知識回顧與實踐,動手比賽和產業應用實踐等。
3.模型訓練
使用Runner,進行相關模型訓練配置,即可啟動模型訓練
# 指定運行設備
use_gpu = True if paddle.get_device().startswith("gpu") else False
if use_gpu:paddle.set_device('gpu:0')
# 學習率大小
lr = 0.001
# 批次大小
batch_size = 64
# 加載數據
train_loader = io.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = io.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = io.DataLoader(test_dataset, batch_size=batch_size)
# 定義網絡
model = resnet19_model
# 定義優化器,這里使用Adam優化器以及l2正則化策略,相關內容在后續會有相應的教程
optimizer = opt.Adam(learning_rate=lr, parameters=model.parameters(), weight_decay=0.005)
# 定義損失函數
loss_fn = F.cross_entropy
# 定義評價指標
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 啟動訓練
log_steps = 3000
eval_steps = 3000
runner.train(train_loader,dev_loader,num_epochs=30,log_steps=log_steps,eval_steps=eval_steps,save_path="best_model.pdparams")4.殘差網絡
-
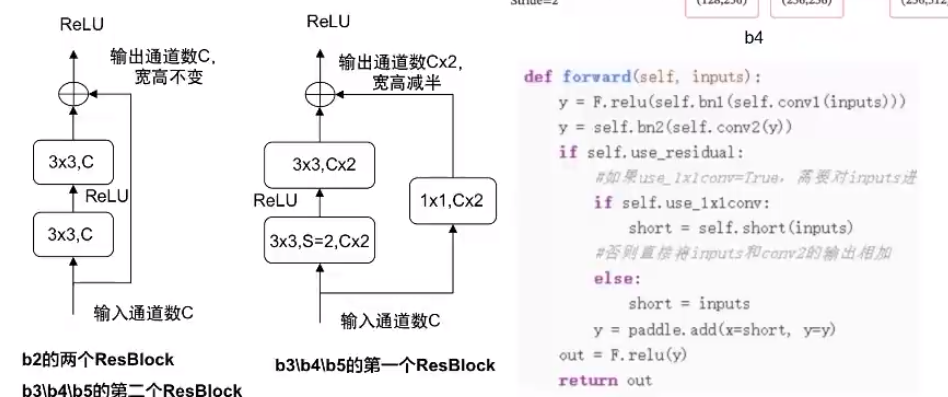
殘差網絡:在神經網絡模型中給非線性層增加直連邊的方式來緩解梯度消失問題,從而使訓練深度神經網絡變得更加容易
-
殘差單元:一個典型的殘差單元由多個級聯的卷積層和一個跨層的直連邊組成
ResBlock f(x) = f(x; θ)+x -
Transformer:加與規范層,
H=LN(H+X) -
Gradient Boosting:
Greedy Function Approximation:A Gradient Boosting Machine,GBDT:Gradient Boosting Decision Tree
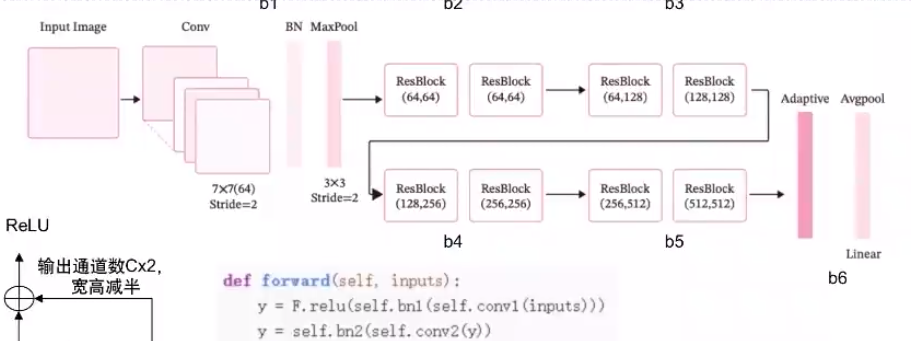
ResNet18整體結構與實現:
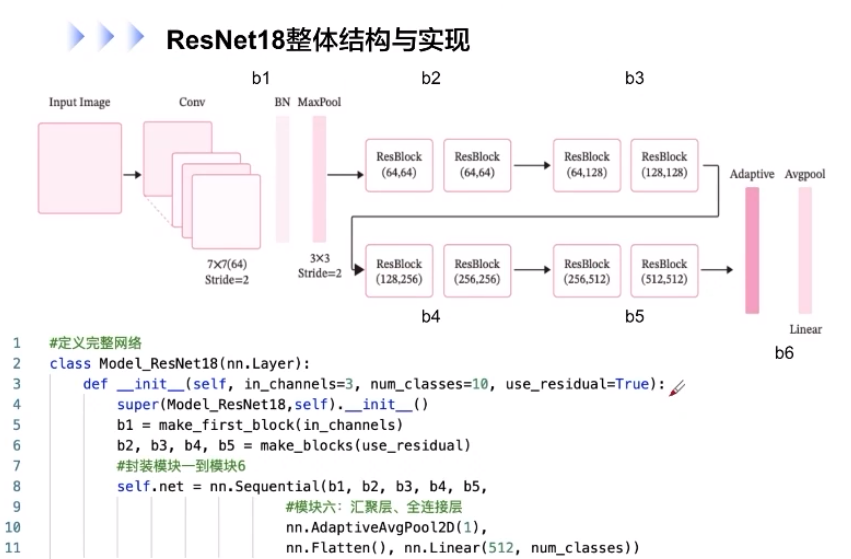
# 定義完整網絡
class Model_ResNet18(nn.Layer):def __init__(self, in_channels=3, num_classes=10, use_residual=Ture):super(Model_ResNet18, self).__init__()b1 = make_first_block(in_channels)b2, b3, b4, b5 = make_blocks(use_residual)# 封裝模板1到模板6self.net = nn.Sequential(b1, b2, b3, b4, b5,# 模塊6:匯聚層、全連接層nn.AdaptiveAvgPool2D(1),nn.Flatten(), nn.Linear(512, num_classes))然后針對構建ResNet18中各模塊,后序會有所介紹,這里就以b1為例,展示一下它相應的代碼
def make_first_block(in_channels):# m模塊1:7*7卷積、批歸一化、匯聚b1 = nn.Sequential(nn.Conv2D(in_channels, 64, kernel_size=7, stride=2, padding=3),nn.BatchNorm2D(64), nn.ReLU(),nn.MaxPool2D(kernel_size=3, stride=2, padding=1))return b1通常而言,特別是是在模型評價中,不帶殘差連接的ResNet18網絡的準確率是遠小于加了殘差連接的神經網絡的,模型效果差別是相當顯著的。
5.卷積神經網絡應用及原理
5.1.卷積神經網絡
卷積一詞我們并不陌生,我們在學習深度學習或者強化學習經常會遇到卷積這個概念。簡而言之,卷積就是將我們的數據進行處理,處理得足夠小,足以讓我們的機器去識別。
在二維卷積算子中,我們的目的是在具體實現上,以互相運算來代替卷積,對于一個輸入矩陣X∈RM*N,使用濾波器W∈RU*V進行運算。
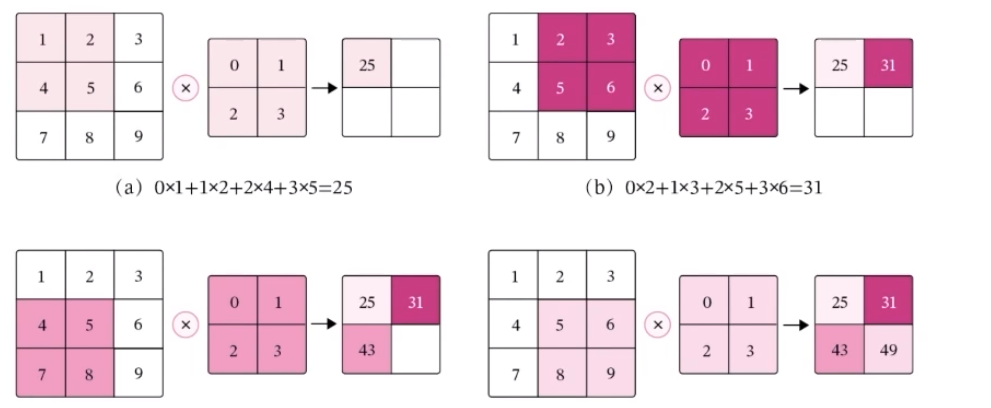
上面的深色區域也就是我們所說的滑動窗口(嘿嘿,情不自禁想起了y總算法基礎課里的滑動窗口一題,那個是一個典型的動態規劃問題),為了實現局部信息到全局信息的融合,通過權值共享實現了參數量的不增加,降低了網絡模型的復雜度,減少了權值的數目。參數的。在整個網絡的訓練過程中,包含權值的卷積核也會隨之更新,直到訓練完成。
輸出特征圖大小:M' = M - U + 1 N' = N - V + 1
特性:
-
局部連接:第i層中的每一個神經元都只和第i-1層中某個局部窗口內的神經元相連,構成一個局部連接網絡。
-
權重共享:所有作為參數的卷積核W∈RU*V對于第i層的所有神經元都是相同的。
二維卷積算子:

可以隨機構造一個二維輸入矩陣
paddle.seed(100)
inputs = paddle.to_tensor([[[1.,2.,3.],[4.,5.,6.],[7.,8.,9.]]])
?
conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input:{}\noutput:{}"format(inputs,outputs))5.2.API說明
API(Application Programming Interface,應用程序編程接口)是一種定義軟件組件之間如何通信的規范。它提供了一種標準化的接口,允許不同的軟件系統之間進行交互和通信。
API通常是一組預先定義的函數、方法、類和對象,開發人員可以使用這些接口來調用軟件組件的功能。API還規定了如何傳遞參數、返回值以及錯誤處理等細節。
API說明通常包括以下內容:
- 接口名稱和功能描述:提供接口的名稱和功能描述,讓開發人員了解該接口的作用和用途。
- 輸入參數說明:詳細說明每個輸入參數的名稱、類型、意義和用法,以確保開發人員正確地使用這些參數。
- 返回值說明:解釋每個返回值的含義和用法,以及在成功或失敗時返回什么樣的數據。
- 錯誤處理說明:描述可能會出現的錯誤和異常情況,并提供相應的處理方法。
- 其他注意事項:提供其他與接口相關的信息和注意事項,例如使用限制、安全要求等。
通過閱讀API說明,開發人員可以更好地理解接口的用途和使用方法,從而更有效地使用API進行軟件開發和集成。
paddle.create_parameter(shape,dtype,attr=None)
功能:創建一個可學習的Parameter變量
輸入:Parameter變量的形狀、數據類型、屬性
輸出:創建的Parameter變量
二維卷積算子的參數量
對于一個輸入矩陣X∈RMxN,使用濾波器W∈RUxV進行運算,卷積核的參數量為:U×V
假設有一個32×32大小的圖像,使用隱藏層神經元個數為1的全連接前饋網絡進行處理:
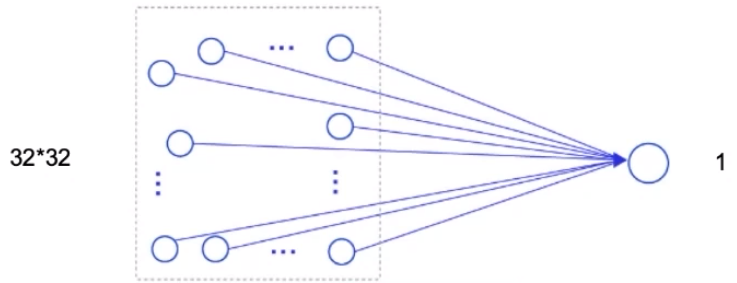
32 * 32 + 1 =1025
使用3 * 3卷積核進行處理,參數量為:9
5.3.二維卷積算子的計算量
計算量:網絡乘加運算總次數
FLOPs=M' * N' * U * V
假設有一個32×32大小的圖像,使用3×3卷積核進行處理,計算量為:
M' = M - U + 1 = 30
N' = N - V + 1 = 30
FL0Ps = M' × N' × U × V = 30 × 30 × 3 × 3 = 8100
5.4.感受野
這個概念也不陌生,是指神經元或感受器能接受刺激的空間范圍。在視覺系統中,它通常指的是視網膜上一個簡單的、沒有特定方向性的感受器(即非方向性光感受器)能接收到的空間范圍。在中樞中,某一神經元的感受野是分布于其胞體和樹突上,是在時間和空間上能被神經元響應的各種形式的光刺激模式(即特定的空間頻率特性)的總和。
就如下面兩個特征圖:
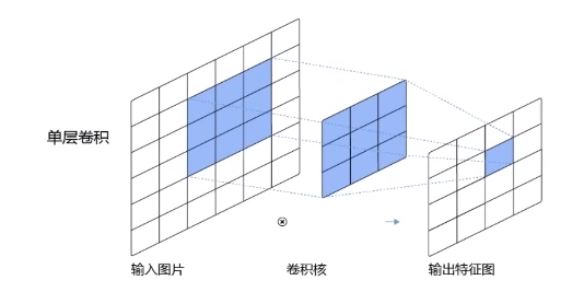
感受野大小:3 x 3
輸出特征圖上的像素點所能感受到的輸入數據的范圍
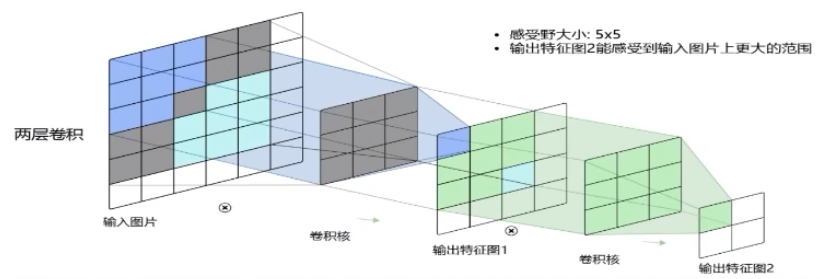
5.5.帶步長和零填充的二維卷積算子
步長(Stride)
在所有維度上每隔S個元素計算一次,S稱為卷積的步長
對于一個輸入矩陣X∈RMxW,使用濾波器W∈RUxV進行運算
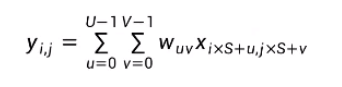
零填充(Zero Padding)
如果不進行填充,當卷積核尺寸大于時,輸出特征會縮減
對輸入進行零填充可以對卷積核的寬度和輸出的大小進行獨立的控制
對于一個輸入矩陣X∈RMxN,使用濾波器W∈RUxV進行運算,步長為S,并進行零填充后,輸出矩陣大小為:
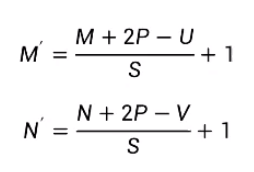
參數量:U x V
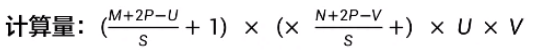
帶步長和零填充的二維卷積算子代碼
class Conv2D(nn.Layer):def __init__(self, kernel_size, stride=1, padding=0,weight_attr=paddle.ParamAttr(initializer=nn.initializer.Constant(value=1.0))):super(Conv2D, self).__init__()self.weight = paddle.create_parameter(shape=[kernel_size,kernel_size],dtype='float32',attr=weight_attr)# 步長self.stride = stride# 零填充self.padding = paddingdef forward(self, X):# 零填充new_X = paddle.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = Xu, v = self.weight.shapeoutput_w = (new_X.shap[1] - u) // self.stride + 1output_h = (new_X.shap[2] - u) // self.stride + 1output = paddle.zeros([X.shape[0], output_w, output_h])for i in range(0, output.shape[1]):for j in range(0, output.shape[2]):output[:, i, j] = paddle.sum(new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*self.weight,axis=[1,2])return outputinputs = paddle.randn(shape=[2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3,padding=1 stride=1,input's shape:{}output's shape:()"format(inputs.shape,outputs.shape))
conv2d_stride Conv2D(kernel_size=3,stride=2,padding=1)
outputs conv2d_stride(inputs)卷積神經網絡
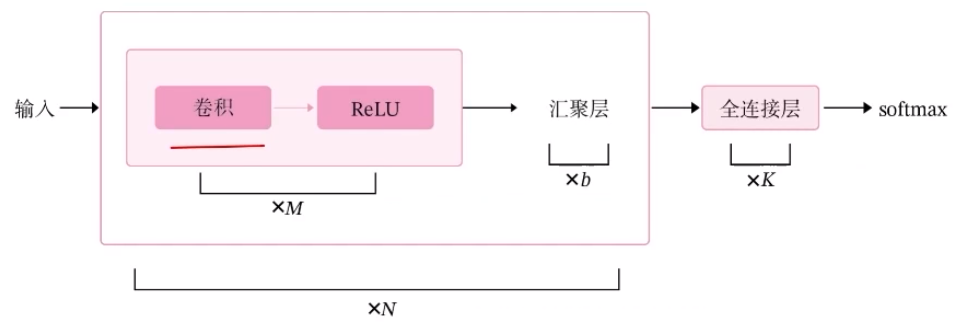
6.卷積層算子
輸入通道:等于輸入特征圖的深度D
例如:輸入是灰度圖像,則輸入通道數為1;輸入是彩色圖像,分別有R、G、B三個通道,則輸入通道數為3;輸入是深度D的特征圖,則輸入通道數為D
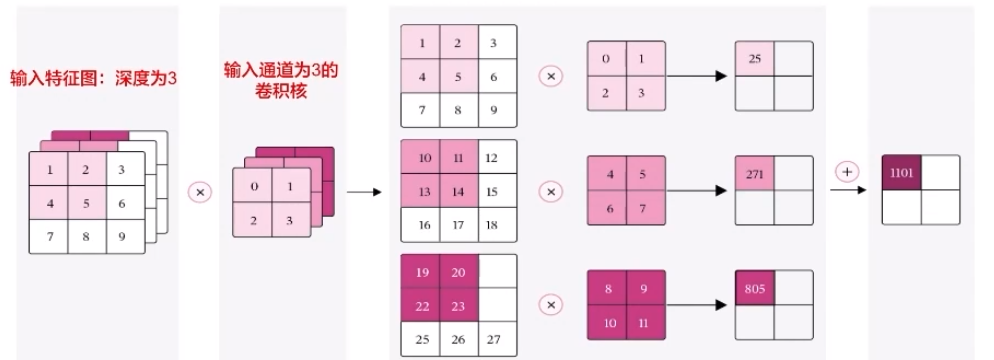
6.1.多通道卷積層算子
class Conv2D(nn.Layer):def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,weight_attr=paddle.ParamAttr(initializer=nn.initializer.Constant(value=1.0)),bias_attr=paddle.ParamAttr(initializer.Constant(value=0.0))):super(Conv2D, self).__init__()#創建卷積核self.weight = paddle.create_parameter(shape=[out_channels, in_channels, kernel_size, kernel_size],dtype='float32',attr=weight_attr)#創建偏置self.bias = paddle.create_parameter(shape=[out_channels, 1],dtype='float32',attr=bias_attr)self.stride = strideself.padding = padding#輸入通道數self.in_channels = in_channels#輸出通道數self.out_channels = out_channels#基礎卷積運算def single_forward(self, X, weight):#零填充new_X = paddle.zeros([X.shape[0],X.shape[1]+2*self.padding,X.shape[2]+2*self.padding])new_X[:,self.padding:X.shape[1]+self.padding,self.padding:X.shape[2]+self.padding]=xu,v weight.shapeoutput_w =(new_X.shape[1]u)//self.stride +1output_h (new_X.shape[2]-v)//self.stride 1output paddle.zeros([X.shape[e],output_w,output_h])for i in range(0,output.shape[1]):for j in range(0, output.shape[2]):output[:, i, j] = paddle.sum(new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*self.weight,axis=[1,2])return output6.2.匯聚層算子
平均匯聚:將輸入特征圖劃分多個為M'×N'大小的區域,對每個區域內的神經元活性值取平均值作為這個區域的表示
最大匯聚:使用輸入特征圖的每個子區域內所有神經元的最大活性值作為這個區域的表示
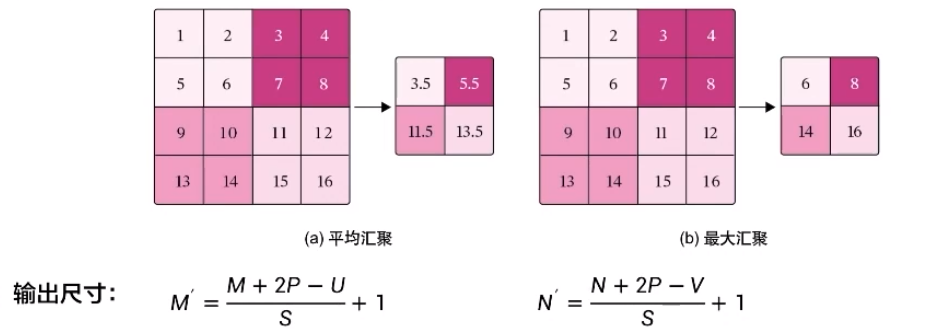
平移不變:當輸入數據做出少量平移時,經過匯聚運算后的大多數輸出還能保持不變。
參數量:0 計算量:最大匯聚為0 平均匯聚為M' x N' x P
6.3.雙向LSTM和注意力機制的文本分類-注意力層
嵌入層:將輸入句子中的詞語轉換成向量表示;
LSTM層:基于雙向LSTM網絡來構建句子中的上下文表示;
注意力層:使用注意力機制從LSTM的輸出中篩選和聚合有效特征;
線性層:輸出層,預測對應的類別得分。
6.4.注意力機制
從N個輸入向量中選擇出和某個特定任務相關的信息。
輸入向量:X=[x1;...;Xn]小,其中Xn是向量,X∈RNxD其中n是序列長度,D表示每個元素的維度
查詢向量:q,任務相關

打分函數
加強模型,雙線性模型
點積模型,縮放點積模型
QKV自注意力的深度代碼解讀
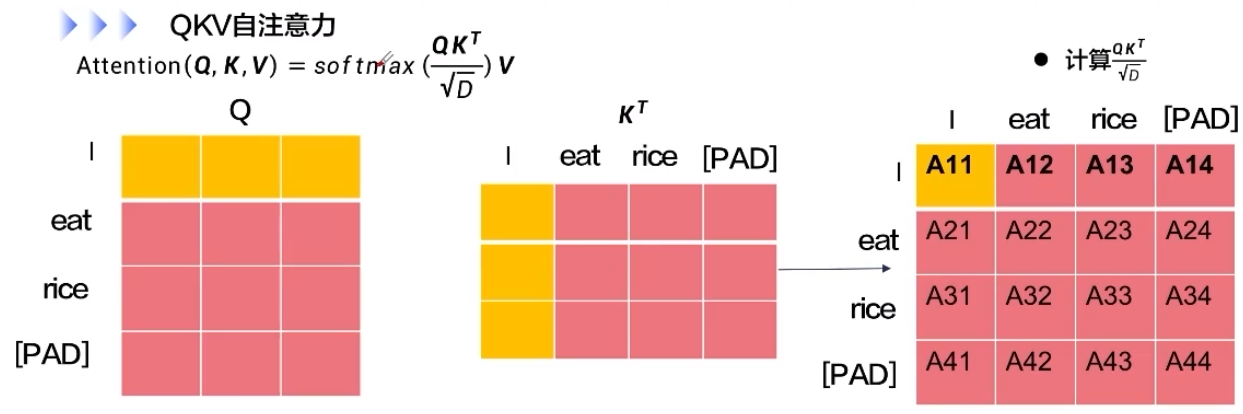


)






)





)



