機器學習｜Softmax 回歸的數學理解及代碼解析

Softmax 回歸是一種常用的多類別分類算法，適用于將輸入向量映射到多個類別的概率分布。在本文中，我們將深入探討 Softmax 回歸的數學原理，并提供 Python 示例代碼幫助讀者更好地理解和實現該算法。

Softmax 回歸數學原理

Softmax 函數將輸入向量的線性得分轉換為每個類別的概率。給定一個輸入向量 x，有如下公式計算 Softmax 函數的輸出：

$$P(y=j\mid x)=\frac{e^{x_j}}{{\sum }_{k=1}^K{e}^{x_k}}$$

其中，$P(y=j\mid x)$ 表示輸入向量 x 屬于類別 j 的概率，$x_j$ 是 x 的第 j 個元素，$K$ 是總的類別數。

Softmax 回歸示例代碼

下面是使用 Python 編寫的一個簡單的 `Softmax 回歸示例代碼：

import numpy as np
import matplotlib.pyplot as pltdef softmax(z):exp_scores = np.exp(z)probs = exp_scores / np.sum(exp_scores)return probs# 生成一組隨機的線性得分
z = np.array([3.0, 1.0, 0.2])# 計算 softmax 函數的輸出
probs = softmax(z)# 打印每個類別的概率
labels = ['Apple', 'Orange', 'Banana']
for label, prob in zip(labels, probs):print(label + ' probability:', prob)# 繪制函數圖像
x = np.arange(-10, 10, 0.1)
y = np.zeros((len(x), len(labels)))for i, val in enumerate(x):z = np.array([val, 1.0, 0.2])probs = softmax(z)y[i] = probsplt.plot(x, y[:, 0], label='Apple')
plt.plot(x, y[:, 1], label='Orange')
plt.plot(x, y[:, 2], label='Banana')
plt.xlabel('Linear Score')
plt.ylabel('Probability')
plt.title('Softmax Regression')
plt.legend()
plt.show() 

在示例代碼中，我們首先定義了一個 softmax 函數，用于計算 Softmax 函數的輸出。然后，我們生成了一個隨機的線性得分向量 z，并調用 softmax 函數獲得每個類別的概率。最后，我們打印出每個類別的概率值。

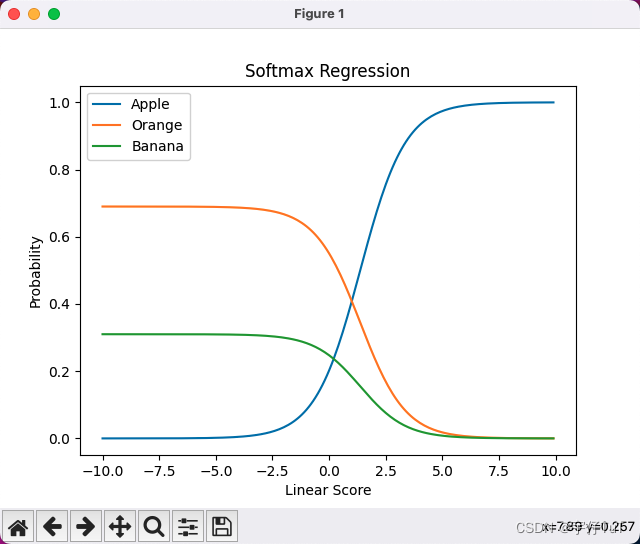
該程序繪制的函數圖像

結語

通過本文，我們詳細講解了 Softmax 回歸的數學原理，并提供了一個簡單的 Python 示例代碼展示了如何實現該算法。希望本文能夠幫助讀者更好地理解 Softmax 回歸，并能夠應用到實際問題中。

如果你對 Softmax 回歸或其他機器學習算法有任何疑問或想法，請在評論區留言，期待與大家的交流討論！