堆

堆簡介

堆是一棵樹，其每個節點都有一個鍵值，且每個節點的鍵值都大于等于/小于等于其父親的鍵值。

每個節點的鍵值都大于等于其父親鍵值的堆叫做小根堆，否則叫做大根堆。STL 中的 priority_queue 其實就是一個大根堆。

（小根）堆主要支持的操作有：插入一個數、查詢最小值、刪除最小值、合并兩個堆、減小一個元素的值。

一些功能強大的堆（可并堆）還能（高效地）支持 merge 等操作。

一些功能更強大的堆還支持可持久化，也就是對任意歷史版本進行查詢或者操作，產生新的版本。

堆的分類

習慣上，不加限定提到「堆」時往往都指二叉堆。

二叉堆

結構
從二叉堆的結構說起，它是一棵二叉樹，并且是完全二叉樹，每個結點中存有一個元素（或者說，有個權值）。

堆性質：父親的權值不小于兒子的權值（大根堆）。同樣的，我們可以定義小根堆。本文以大根堆為例。

由堆性質，樹根存的是最大值（getmax 操作就解決了）。

過程

插入操作

插入操作是指向二叉堆中插入一個元素，要保證插入后也是一棵完全二叉樹。

最簡單的方法就是，最下一層最右邊的葉子之后插入。

如果最下一層已滿，就新增一層。

插入之后可能會不滿足堆性質？

向上調整：如果這個結點的權值大于它父親的權值，就交換，重復此過程直到不滿足或者到根。

可以證明，插入之后向上調整后，沒有其他結點會不滿足堆性質。

向上調整的時間復雜度是 $O(logn)$的。

刪除操作

刪除操作指刪除堆中最大的元素，即刪除根結點。

但是如果直接刪除，則變成了兩個堆，難以處理。

所以不妨考慮插入操作的逆過程，設法將根結點移到最后一個結點，然后直接刪掉。

然而實際上不好做，我們通常采用的方法是，把根結點和最后一個結點直接交換。

于是直接刪掉（在最后一個結點處的）根結點，但是新的根結點可能不滿足堆性質……

向下調整：

在該結點的兒子中，找一個最大的，與該結點交換，重復此過程直到底層。

可以證明，刪除并向下調整后，沒有其他結點不滿足堆性質。

時間復雜度 $O(logn)$。

增加某個點的權值

很顯然，直接修改后，向上調整一次即可，時間復雜度為 $O(logn)$。

實現

我們發現，上面介紹的幾種操作主要依賴于兩個核心：向上調整和向下調整。

考慮使用一個序列 $h$ 來表示堆。$h_i$ 的兩個兒子分別是 $h_2$${}_i$ 和 $h_2$${}_i$${}_{+}$${}_1$，$1$ 是根結點：

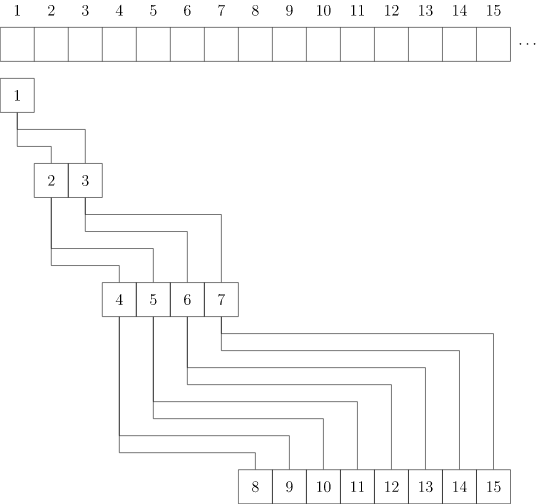
參考代碼：

void up(int x) {while (x > 1 && h[x] > h[x / 2]) {swap(h[x], h[x / 2]);x /= 2;}
}void down(int x) {while (x * 2 <= n) {t = x * 2;if (t + 1 <= n && h[t + 1] > h[t]) t++;if (h[t] <= h[x]) break;std::swap(h[x], h[t]);x = t;}
}

建堆

考慮這么一個問題，從一個空的堆開始，插入 n 個元素，不在乎順序。

直接一個一個插入需要 $O(nlogn)$ 的時間，有沒有更好的方法？

方法一：使用 decreasekey（即，向上調整）

從根開始，按 BFS 序進行。

void build_heap_1() {for (i = 1; i <= n; i++) up(i);
}

為啥這么做：對于第 k 層的結點，向上調整的復雜度為 $O(k)$ 而不是 $O(logn)$。

總復雜度：$log1$ + $log2$ + … + $logn$ = $O(nlogn)$。

（在「基于比較的排序」中證明過）

方法二：使用向下調整

這時換一種思路，從葉子開始，逐個向下調整

void build_heap_2() {for (i = n; i >= 1; i--) down(i);
}

換一種理解方法，每次「合并」兩個已經調整好的堆，這說明了正確性。

注意到向下調整的復雜度，為 $O(logn?k)$，另外注意到葉節點無需調整，因此可從序列約 n/2 的位置開始調整，可減少部分常數但不影響復雜度。

之所以能 $O(n)$ 建堆，是因為堆性質很弱，二叉堆并不是唯一的。
要是像排序那樣的強條件就難說了。

應用

對頂堆

這個問題可以被進一步抽象成：動態維護一個序列上第 $k$ 大的數，$k$ 值可能會發生變化。

對于此類問題，我們可以使用對頂堆這一技巧予以解決（可以避免寫權值線段樹或$BST$帶來的繁瑣）。

對頂堆由一個大根堆與一個小根堆組成，小根堆維護大值即前 $k$ 大的值（包含第 $k$ 個），大根堆維護小值即比第 $k$ 大數小的其他數。

這兩個堆構成的數據結構支持以下操作：

1.維護：當小根堆的大小小于 $k$ 時，不斷將大根堆堆頂元素取出并插入小根堆，直到小根堆的大小等于 $k$；當小根堆的大小大于 $k$ 時，不斷將小根堆堆頂元素取出并插入大根堆，直到小根堆的大小等于 $k$；

2.插入元素：若插入的元素大于等于小根堆堆頂元素，則將其插入小根堆，否則將其插入大根堆，然后維護對頂堆；

3.查詢第 k 大元素：小根堆堆頂元素即為所求；

4.刪除第 k 大元素：刪除小根堆堆頂元素，然后維護對頂堆；

顯然，查詢第 $k$ 大元素的時間復雜度是 $O(1)$ 的。由于插入、刪除或調整 $k$ 值后，小根堆的大小與期望的 $k$ 值最多相差 $1$，故每次維護最多只需對大根堆與小根堆中的元素進行一次調整，因此，這些操作的時間復雜度都是 $O(logn)$ 的。

其他：

配對堆:

詳見：鏈接: 數據結構——配對堆

左偏樹:

詳見后文。