??????

預備知識

????? 1）RSA是第一個比較完善的公開密鑰算法，它既能用于加密，也能用于數字簽名。RSA以它的三個發明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名，這個算法經受住了多年深入的密碼分析，雖然密碼分析者既不能證明也不能否定RSA的安全性，但這恰恰說明該算法有一定的可信性，目前它已經成為最流行的公開密鑰算法。

????? 2) 什么是“素數”？

????? 素數是這樣的整數，它除了能表示為它自己和1的乘積以外，不能表示為任何其它兩個整數的乘積。例如，15＝3＊5，所以15不是素數；又如，12＝6＊2＝4＊3，所以12也不是素數。另一方面，13除了等于13＊1以外，不能表示為其它任何兩個整數的乘積，所以13是一個素數。素數也稱為“質數”。

????? 3）什么是“互質數”（或“互素數”）？

????? 數學教材對互質數是這樣定義的：“公約數只有1的兩個數，叫做互質數。”這里所說的“兩個數”是指自然數。

? ?? ? ???? 判別方法主要有以下幾種（不限于此）：

　　　　?（1）兩個質數一定是互質數。例如，2與7、13與19。

　　　　（2）一個質數如果不能整除另一個合數，這兩個數為互質數。例如，3與10、5與26。

????? 　　（3）1不是質數也不是合數，它和任何一個自然數在一起都是互質數。如1和9908。

????????????? （4）相鄰的兩個自然數是互質數。如15與16。

???? ? ? ? ?? （5）相鄰的兩個奇數是互質數。如49與51。

??? ? ? ? ??? （6）大數是質數的兩個數是互質數。如97與88。

?? ? ? ? ? ?? （7）小數是質數，大數不是小數的倍數的兩個數是互質數。如7和16。

? ? ? ? ? ??? （8）兩個數都是合數（二數差又較大），小數所有的質因數，都不是大數的約數，這兩個數是互質數。如357與715，357=3×7×17，而3、7和17都不是715的約數，這兩個數為互質數。等等。

????? 4）非對稱加密算法（asymmetric cryptographic algorithm）又名“公開密鑰加密算法”，非對稱加密算法需要兩個密鑰：公開密鑰（publickey）和私有密鑰（privatekey）。公開密鑰與私有密鑰是一對，如果用公開密鑰對數據進行加密，只有用對應的私有密鑰才能解密；如果用私有密鑰對數據進行加密，那么只有用對應的公開密鑰才能解密。因為加密和解密使用的是兩個不同的密鑰，所以這種算法叫作非對稱加密算法。

????? 5) 什么是模指數運算？

????? 模運算是整數運算，有一個整數m，以n為模做模運算，即m mod n。怎樣做呢？讓m去被n整除，只取所得的余數作為結果，就叫做模運算。例如，10 mod 3=1；26 mod 6=2；28 mod 2 =0等等。模指數運算就是先做指數運算，取其結果再做模運算。如53 mod 7=125 mod 7=6。

????? 6）RSA安全性分析

????? 在公布RSA算法之后，在使用RSA密碼體制和分析RSA算法發現了一系列的算法本身脆弱性及其存在的問題。

????? （1）RSA公鑰密碼體制在加密或解密變化中涉及大量的數值計算，其加密和解密的運算時間比較長，這比數據加密標準DES的計算量開銷大，在一定程度上限制了它的應用范圍，以致于實際使用RSA密碼體制無法用軟件產品，必須用超大規模集成電路的硬件產品。

????? （2）雖然提高N=P*Q的位數會大大提高RSA密碼體制的安全性，但其計算量呈指數增長，以致使其實現的難度增大，實用性降低。

????? （3）RSA公鑰密碼體制的算法完整性（指密鑰控制加密或解密變換的唯一性）和安全性（指密碼算法除密鑰本身外，不應該存在其它可破譯密碼體制的可能性）沿有等進一步完善。

????? （4）RSA算法面臨著數學方法的進步和計算機技術飛躍發展帶來的破譯密碼能力日趨增強的嚴重挑戰。因子分解問題有了長跑的發展，1995年人類成功地分解了128位十進制數RSA密碼算法，破譯512位長的RSA指日可待。

???? 盡管如此，自1978年RSA算法公布以來，公開密鑰密碼已從理論研究進入實際應用研究階段。RSA公開密鑰密碼算法在信息交換過程中使用比較廣泛，安全性比較高。以當前的計算機水平，如選擇1024位長的密鑰（相當于300位十進制數字）就認為是無法攻破的。

????? 7）CAP(Cryptographic Analysis Program)是由DR. Richard Spillman專門為教學而研制的密碼制作與分析工具，已經在美國的很多高校得到了廣泛地使用，受到了密碼學習者的普遍歡迎。

公鑰和私鑰的簡單理解????

初學的話對于公鑰和私鑰的理解是一個問題（我自己就是這樣(*/ω＼*)，所以我們再來說一下對于公鑰和私鑰的一個簡單的認識。我在網上找了一篇我理解了下面放出來讓大家參考一下，?????????????????????? 原文地址：https://blog.csdn.net/tabactivity/article/details/49685319

一、公鑰加密?
假設一下，我找了兩個數字，一個是1，一個是2。我喜歡2這個數字，就保留起來，不告訴你們(私鑰），然后我告訴大家，1是我的公鑰。

我有一個文件，不能讓別人看，我就用1加密了。別人找到了這個文件，但是他不知道2就是解密的私鑰啊，所以他解不開，只有我可以用
數字2，就是我的私鑰，來解密。這樣我就可以保護數據了。

我的好朋友x用我的公鑰1加密了字符a，加密后成了b，放在網上。別人偷到了這個文件，但是別人解不開，因為別人不知道2就是我的私鑰，
只有我才能解密，解密后就得到a。這樣，我們就可以傳送加密的數據了。

? 二、私鑰簽名
如果我用私鑰加密一段數據（當然只有我可以用私鑰加密，因為只有我知道2是我的私鑰），結果所有的人都看到我的內容了，因為他們都知
道我的公鑰是1，那么這種加密有什么用處呢？

但是我的好朋友x說有人冒充我給他發信。怎么辦呢？我把我要發的信，內容是c，用我的私鑰2，加密，加密后的內容是d，發給x，再告訴他
解密看是不是c。他用我的公鑰1解密，發現果然是c。
這個時候，他會想到，能夠用我的公鑰解密的數據，必然是用我的私鑰加的密。只有我知道我得私鑰，因此他就可以確認確實是我發的東西。
這樣我們就能確認發送方身份了。這個過程叫做數字簽名。當然具體的過程要稍微復雜一些。用私鑰來加密數據，用途就是數字簽名。

舉例

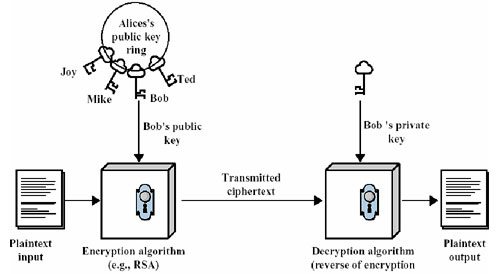
比如有兩個用戶Alice和Bob，Alice想把一段明文通過雙鑰加密的技術發送給Bob，Bob有一對公鑰和私鑰，那么加密解密的過程如下：

1. Bob將他的公開密鑰傳送給Alice。
2. Alice用Bob的公開密鑰加密她的消息，然后傳送給Bob。
3. Bob用他的私人密鑰解密Alice的消息。

　　??? 上面的過程可以用下圖表示，Alice使用Bob的公鑰進行加密，Bob用自己的私鑰進行解密。

RSA加解密算法的原理

? 首先產生密鑰，過程如下：

? 隨機產生兩個長度為K/2位的素數P 和 Q；

? 計算公鑰 publicKey=P*Q;(publicKey 是k位的長度)

? 隨機產生一個加密密鑰 keyE, 2<=keyE<=Φ(n)-1其中GCD(keyE, Φ(n))=1；注：這是保證解密密鑰keyE keyD mod Φ(n)=1 有解的充要條件，Φ(n)稱為n的歐拉函數,值為: Φ(n)=(P-1)(Q-1)

? 求解解密密鑰keyD=keyE-1 mod (n) ，keyE-1為解密密鑰keyD的逆元，此公式原方程為(keyE*keyD mod (n)=1)

? 由此公鑰，加密密鑰，解密密鑰全部產生。

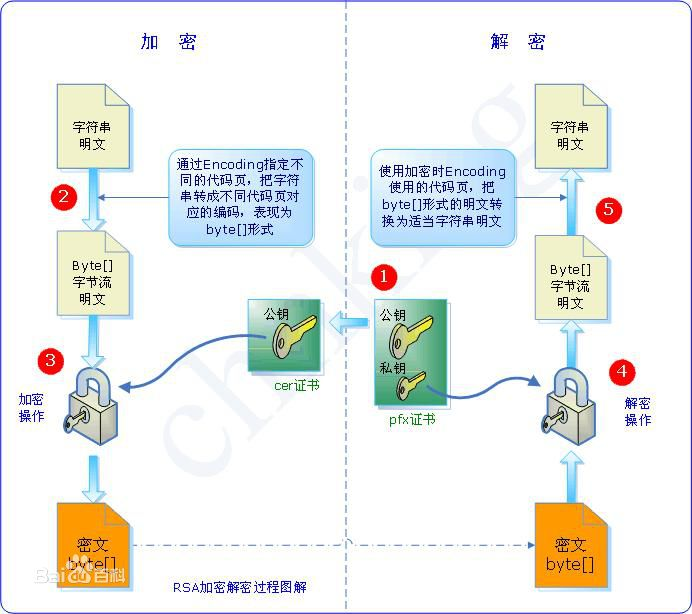
? 其次，對明文加密或對密文進行解密,過程如下：

? (1) 加密: C = MkeyE mod publicKey;其中M表示明文，C表示密文

? (2) 解密: M = CkeyD mod publicKey. 其中M表示明文，C表示密文

　　RSA加密學習的簡單例子（轉載）

我在網上看到一篇文章如下，通過簡單的舉例，我更理解了RSA算法的神奇，作者的舉例很棒。

在RSA中，最大值(稱為max)由隨機挑選的兩個素數相乘而得。公鑰和密鑰在0和最大值之間挑選（稱為pub和priv）。為了加密一個數字，讓這個數字自己乘自己pub次，并確保當乘積大于最大值時能夠回折（像時鐘一樣）。解密時，再用這個加密得到的結果自己乘自己priv次，便能退回到原始的數字。這是一件很神奇的事情！但是它確實被實現了。

為了創建RSA密鑰對，首先得隨機的挑選兩個素數來計算出max。然后從0到max中再挑選出公鑰pub，只要知道兩個素數，那么就能夠從pub中算出私鑰。這就是為什么因式分解與破解RSA有關—對max的因式分解，可以得到兩個素數，這樣你便能夠通過pub計算出某人的私鑰，從而來解密消息。

讓我們舉一個更加具體的例子吧。挑選素數13和7。他們積為91，也就是max。從0到91中挑選5作為pub來加密。利用算法Extended Euclidean，輸入參數:7，13，5，得到私鑰是29。

三個參數(max:91,pub:5,priv:29)定義了RSA系統。這時，可以取一個數字，通過乘自己5次來加密自己，然后取這個結果乘自己29次來回到原來的數字。

讓我們來加密“CLOUD”。為了能夠用數學來表示一個消息，我們必須將字母轉變為數字。一個常用的轉換方法是UTF-8。每個字母對應一個數字，如下圖：