給定 N，想象一個凸 N 邊多邊形，其頂點按順時針順序依次標記為 A[0], A[i], …, A[N-1]。

假設您將多邊形剖分為 N-2 個三角形。對于每個三角形，該三角形的值是頂點標記的乘積，三角剖分的分數是進行三角剖分后所有 N-2 個三角形的值之和。

返回多邊形進行三角剖分后可以得到的最低分。

示例 1：

輸入：[1,2,3]
輸出：6
解釋：多邊形已經三角化，唯一三角形的分數為 6。

圖解狀態轉移

dp[i][j]代表區間（i，j）內多邊形進行三角剖分后可以得到的最低分

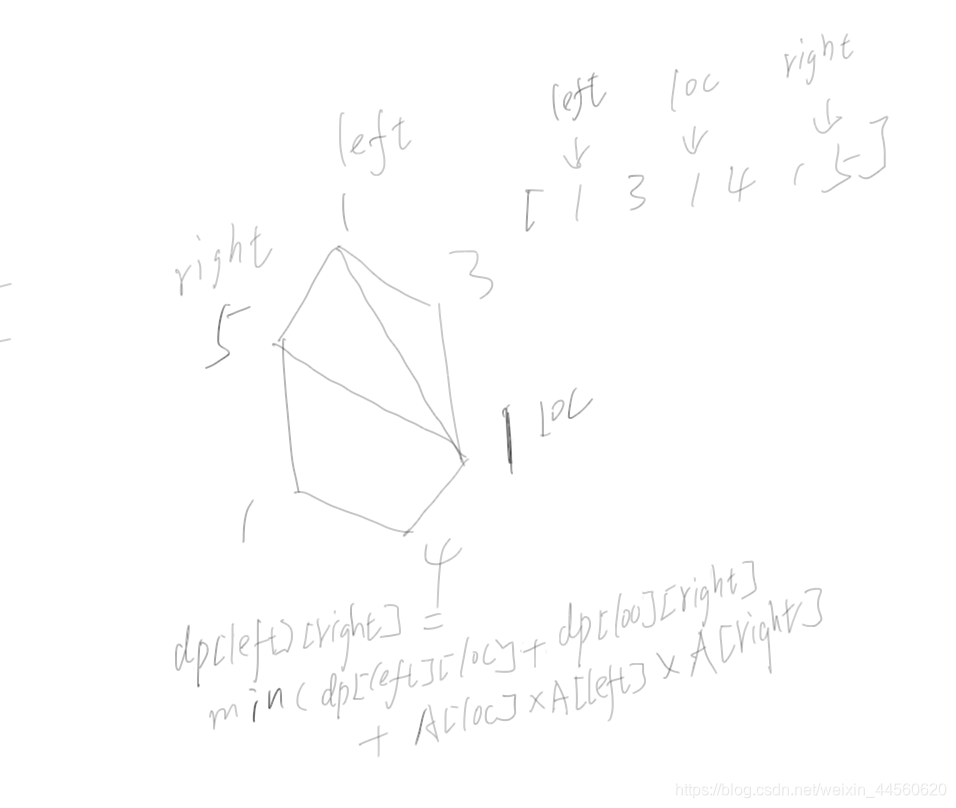
代碼

class Solution {public int minScoreTriangulation(int[] A) {int n=A.length;int[][] dp=new int[n][n];for(int i=0;i<n;i++)Arrays.fill(dp[i],Integer.MAX_VALUE);for(int i=0;i<n;i++)dp[i][(i+1)%n]=0;for(int len=2;len<n;len++)for (int left=0;left<n;left++){int right=(left+len)%n;for(int loc=(left+1)%n;loc!=right;loc=(loc+1)%n)dp[left][right]= Math.min(dp[left][right],dp[left][loc]+dp[loc][right]+A[loc]*A[left]*A[right]);}return dp[0][n-1];}
}