本系列博文為深度學習/計算機視覺論文筆記，轉載請注明出處

標題：Generative Adversarial Nets

鏈接：Generative Adversarial Nets (nips.cc)

摘要

我們提出了一個通過**對抗（adversarial）**過程估計生成模型的新框架，在其中我們同時訓練兩個模型：

一個生成模型G，捕獲數據分布
一個判別模型D，估計樣本來自訓練數據還是G的概率。

G的訓練過程是最大化D犯錯誤的概率。

該框架對應于一個極小極大的兩人博弈。

在任意函數G和D的空間中，存在一個唯一解決方案，G恢復訓練數據分布，D在任何地方都等于1/2。在G和D由多層感知機定義的情況下，可以通過反向傳播訓練整個系統。在訓練或生成樣本期間，不需要任何馬爾可夫鏈或展開的近似推理網絡。

實驗通過生成樣本的定性和定量評估展示了該框架的潛力。

1 引言

深度學習的作用是發現豐富的、層次化的模型[2]，它們表示人工智能應用中遇到的數據類型的概率分布，例如自然圖像、包含語音的音頻波形和自然語言語料庫中的符號。

到目前為止，深度學習最引人注目的成功涉及判別模型，通常是將高維、豐富的感覺輸入映射到類標簽[14, 20]的模型。這些引人注目的成功主要基于反向傳播和隨機失活算法，使用分段線性單元[17, 8, 9]，它們具有特別良好的梯度行為。

深度生成模型的影響較小，這是由于在最大似然估計和相關策略中出現的許多難以近似的概率計算，以及在生成環境中難以利用分段線性單元的好處所造成的。我們提出了一種新的生成模型估計過程，可以避開這些困難。¹

在所提出的對抗網絡框架中，生成模型與一個敵手相對立：

一個判別模型，學會判斷樣本是來自模型分布還是數據分布。生成模型可以被看作與一組偽造者相類似，試圖生產假貨幣并在不被檢測的情況下使用它
判別模型則與警察相類似，試圖檢測偽造貨幣

這個游戲中的競爭推動兩個團隊改進其方法，直到偽造品與真品無法區分。

該框架可以為許多種模型和優化算法產生特定的訓練算法。

在本文中，我們探討了生成模型通過多層感知機（MLP）傳遞隨機噪聲生成樣本，而判別模型也是多層感知機的特殊情況。我們將此特殊情況稱為對抗網絡（adversarial nets）。

在這種情況下，我們可以僅使用高度成功的反向傳播和隨機失活算法[17]來訓練兩個模型，并僅使用前向傳播從生成模型中抽樣。不需要近似推斷或馬爾可夫鏈。

2 相關工作

直到現在，深度生成模型的大部分工作都集中在提供有規范參數的概率分布函數，然后可以通過最大化對數似然函數來訓練模型上。

在這類模型中，可能最成功的是深度玻爾茲曼機（deep Boltzmann machine）[25]。
這類模型通常具有難以處理的似然函數，因此需要對似然梯度進行多次近似。

這些困難促使“生成機（generative machines）”模型的發展——

這些模型不顯式地表示似然函數，但能夠從所需分布中生成樣本。
生成隨機網絡[4]就是一個生成機的例子，它可以通過精確的反向傳播進行訓練，而不需要像玻爾茲曼機那樣進行多次近似。

本文通過消除生成隨機網絡中使用的馬爾可夫鏈，擴展了生成機的思想。

我們的工作通過利用以下觀察，利用生成過程進行導數的反向傳播：
$\lim_{\sigma\rightarrow0}\nabla_{\pmb{x}}\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^{2}\pmb{I})}f(\pmb{x}+\epsilon)=\nabla_{\pmb{x}}f(\pmb{x})$

譯者注：上述公式的意思是對 $f$ 的期望求導等價于對 $f$ 自己求導，這也是為什么作者會利用誤差的反向傳遞對GAN進行求解

當時，我們不知道Kingma和Welling [18]以及Rezende等人[23]已經開發了更通用的隨機反向傳播規則，可以通過有限方差的高斯分布進行反向傳播，并且可以反向傳播到協方差參數以及均值參數。

這些反向傳播規則可以讓我們學習生成器的條件方差，在本文中我們將其視為超參數。

Kingma和Welling [18]以及Rezende等人[23]使用隨機反向傳播來訓練變分自動編碼器（variational autoencoders，VAEs）。

與GAN不同，VAE將一個可微分的生成器網絡與第二個神經網絡配對。
不同于GAN，VAE中的第二個網絡是一個執行近似推斷的識別模型。
GAN需要通過可見單元進行微分，因此無法對離散數據建模，而VAE需要通過隱藏單元進行微分，因此無法具有離散潛變量。

還存在其他類似VAE的方法[12, 22]，但與我們的方法關聯性較小。

先前的工作也采用了使用判別標準來訓練生成模型的方法[29, 13]。這些方法對于深度生成模型來說是難以處理的，因為它們涉及概率的比值，而這些比值不能通過將概率下界的變分近似進行近似來處理。

噪聲對比估計（Noise-contrastive estimation，NCE）[13]涉及通過學習使模型對來自固定噪聲分布的數據具有區分性的權重來訓練生成模型。

使用先前訓練過的模型作為噪聲分布允許訓練一系列質量逐漸提高的模型。這可以看作是一種非正式的競爭機制，類似于對抗網絡游戲中使用的正式競爭機制。
NCE的關鍵局限在于其“鑒別器（discriminator）”是由噪聲分布和模型分布的概率密度比率定義的，因此需要能夠評估并反向傳播這兩個密度。

先前的工作使用了兩個神經網絡相互競爭的一般概念。最相關的工作是可預測性最小化（predictability minimization，下稱PM）[26]。在可預測性最小化中，神經網絡中的每個隱藏單元被訓練得與第二個網絡的輸出不同，而這第二個網絡根據所有其他隱藏單元的值來預測該隱藏單元的值。

譯者注：可預測性最小化是一種神經網絡訓練方法，旨在使隱藏單元在給定其他隱藏單元的值的情況下與另一個網絡的輸出不同。具體而言，第二個網絡會預測某個隱藏單元的值，而這個隱藏單元是在網絡中的一個特定部分。通過訓練隱藏單元與預測的值不同，可預測性最小化試圖確保網絡的隱藏表示在進行某項任務時具有統計上的獨立性。這有助于提高網絡的表達能力和泛化性能。

本文與可預測性最小化有三個重要的區別：

在本文中，**網絡之間的競爭是唯一的訓練準則，**足以訓練網絡。可預測性最小化只是一種鼓勵神經網絡的隱藏單元在完成其他任務的同時具有統計獨立性的正則化器，它不是主要的訓練準則。
競爭的性質是不同的。在可預測性最小化中，比較了兩個網絡的輸出，其中一個網絡試圖使輸出相似，而另一個網絡試圖使輸出不同。所涉及的輸出是一個單一標量。在GAN中，一個網絡產生一個豐富的高維向量，用作另一個網絡的輸入，并試圖得出一個另一個網絡不知道如何處理的輸入。
學習過程的規范是不同的。可預測性最小化被描述為一個要最小化的目標函數的優化問題，學習接近目標函數的最小值。**GAN基于極小極大博弈而不是優化問題，并且具有一個值函數，其中一個代理試圖最大化，而另一個代理試圖最小化。**游戲在一個鞍點終止，該鞍點對于一個玩家的策略是一個最小值，對于另一個玩家的策略是一個最大值。

有時人們會將GAN錯誤地與相關概念“對抗性樣本（adversarial examples）”[28]混淆。

對抗性樣本是通過對分類網絡的輸入直接使用基于梯度的優化方法找到的例子，目的是找到與數據相似但被錯誤分類的例子。
這與本文的工作不同，因為對抗性樣本不是一種訓練生成模型的機制。相反，對抗性樣本主要是用于分析工具，用于展示神經網絡的行為方式，即使兩個圖像在人類觀察者看來幾乎無法區分，神經網絡也會自信地對它們進行不同的高置信度分類。
這種對抗性樣本的存在確實暗示著GAN訓練可能是低效的，因為它們表明現代判別網絡可以自信地識別一類，而無需模擬出該類別的任何人類可感知屬性。

3 對抗網絡

對抗模型框架在模型都是多層感知機（MLP）時最直接應用。

為了學習生成器的數據 $\pmb{x}$ 上的分布 $p_g$ ，我們在輸入噪聲變量 $p_z(z)$ 上定義一個先驗，然后將映射的數據空間表示為 $G(z;\theta_g)$ ，其中 $G$ 是一個由參數 $\theta_g$ 表示的多層感知機的可微函數。
我們還定義了第二個多層感知機 $D(\pmb{x};\theta_d)$ ，其輸出一個標量。 $D(\pmb{x})$ 代表了 $\pmb{x}$ 來自真實數據而不是生成分布 $p_g$ 的概率。

我們訓練 $D$ 以最大化將正確標簽分配給訓練示例和來自 $G$ 的樣本的概率。

我們同時訓練 $G$ 以最小化 $\log(1-D(G(z)))$ 。

譯者注：可以對上述內容進行更生動的描述。

GAN的目的就是要得到最強大的判別器（D）和強大的生成器（G）

假如需要使用某種方法模仿某游戲渲染畫面，比如要渲染出符合某分布的（比如角色陣亡時的）、 $x$ 個像素（ $x$ 維）的畫面 $\pmb{x}$ ，可以有兩種方法：

反匯編游戲程序，了解到具體每行代碼對于每幀畫面生成所具體產生的作用，如“人物造型”、“對象移動”等，以期對畫面分布的生成進行完美的建模。
定義若干個變量（即一個若干維的變量），然后假定認為這若干維的變量通過某種函數關系，共同影響了最終生成數據 $\pmb{x}$ 的分布情況。

前者類似“相關工作”中所提到的“擬合似然函數”的方法，即“追根溯源”的方法，這種方法解釋性很強，可以很好地解釋出每個參數對于最終結果生成所產生的影響，但是操作難度較高，也難找到合適的似然函數。

后者就有點類似于“多層感知機（MLP）”的方法了，理論上來說，MLP可以擬合任意函數的表達，只是可解釋性差。雖然我不知道從游戲代碼到畫面其背后到底是個什么映射關系，但是我估摸著這若干維的參數就足以表達這內容背后隱藏的邏輯了。

只不過我不會知道那若干維的參數之中的每一個，最終對結果 $\pmb{x}$ 到底產生了怎樣的影響，以及每個參數具體有什么含義而已。

整理一下。論文當中的各個變量可以作如下解釋：

數據 $\pmb{x}$ 的分布規律 $p_g$ ，這是最終要得到的結果

生成器 $G(z;\theta_g)$
輸入：取自隨機噪聲 $p_z(z)$ 的初始化數據 $z$
參數： $\theta_g$
輸出： $\pmb{x}$ （如，上例中 $x$ 維的畫面 $\pmb{x}$ ）
優秀的生成器 $G$ ，能夠盡可能生成
更接近真實數據的 $\pmb{x}$
更接近真實分布的 $p_g$

判別器 $D(\pmb{x};\theta_d)$
輸入： $\pmb{x}$
參數： $\theta_d$
輸出：一個標量，表示 $\pmb{x}$ 來自真實數據而非生成分布 $p_g$ 中取樣的概率。
$\pmb{x}$ 越可能來自于真數據，輸出 $D(\pmb{x})$ 越接近 $1$
$\pmb{x}$ 越可能來自于生成器，輸出 $D(\pmb{x})$ 越接近 $0$

優秀的判別器 $D$ ，能夠盡可能判斷出
$\pmb{x}$ 的來源是生成器？
$\pmb{x}$ 的來源是真實分布的采樣？

訓練GAN就是要同時訓練 $G$ 和 $D$ ，并期望都達到優秀標準。

為了訓練出更好的 $G$ ，作者提出了一種衡量標準，即 $\log(1-D(G(z)))$ ，要求這個式子表達的內容盡可能小，下面我們仔細一下分析這個式子：

$z$ 表示初始化的隨機輸入
$G (z)$ 表示生成器生成的結果，期望這個結果更接近真實分布中的采樣
即期望讓生成器 $G$ 造出更“真”的假數據。

$D (G (z))$ 表示使用判別器 $D$ 判別生成器 $G$ 所生成的結果，期望這個結果更接近 $1$
即期望讓判別器 $D$ 盡可能誤以為結果 $G (z)$ 為來自真實分布的采樣

只有當 $D (G (z))$ 越接近 $1$ 時， $\log(1-D(G(z)))$ 才會越接近負無窮（ $-\infty$ ）
這就是文中說的要“最小化 $\log(1-D(G(z)))$ ”的原因

換句話說， $D$ 和 $G$ 玩以下兩人極小極大游戲（two-player minimax game），價值函數為 $V (G, D)$ ：

$\mathop{\min}\limits_{G}\mathop{\max}\limits_{D}V(D,G)=\mathbb{E}_{x\sim{p_{\text{data}}(x)}}[\log D(x)]+\mathbb{E}_{z\sim{p_{z}(x)}}[\log(1 - D(G(z)))]\tag{1}$

譯者注：式中不寫 $V (G, D)$ 而寫 $V (D, G)$ ，應該是作者筆誤。

$\mathbb{E}_{x\sim{p_{\text{data}}(x)}}[\log D(x)]$ 中的 $x$ 采樣于真實值的分布
在判別器 $D$ 很完美的情況下，應該能識別得出所有 $x$ 都是來自于真實分布的采樣
$D (x)$ 應該是趨向于 $1$ 的， $\log D(x)$ 就應該是趨向于 $0$ 的
那么該期望就應該是趨向于 $0$ 的

$\mathbb{E}_{z\sim{p_{z}(x)}}[\log(1 - D(G(z)))]$ 中的 $z$ 采樣于隨機噪聲 $p_z(z)$
在生成器 $G$ 和判別器 $D$ 都很完美的情況下， $D$ 應該能識別得出所有 $G (z)$ 都是來自于生成器的結果
$D (G (z))$ 應該是趨向于 $0$ 的， $\log(1-D(G(z)))$ 就應該也是趨向于 $0$ 的
那么該期望也應該是趨向于 $0$ 的

$\mathop{\max}\limits_{D}$ 表示期望使得 $D$ 盡量不犯錯，即要最大化 $D$ 的值。
$\mathop{\min}\limits_{G}$ 表示期望 $G$ 能使 $D$ 盡量犯錯，即要最小化 $G$ 的值。

在下一節中，我們將提供對抗網絡的理論分析，本質上顯示訓練標準允許在給予 $G$ 和 $D$ 足夠容量的情況下，即在非參數限制下，恢復數據生成分布。

對于一種不太正式、但是更好理解的方法解釋，請參見圖1。

圖1：GAN通過同時更新判別分布（ $D$ ，藍色，虛線）來進行訓練，以便它能夠區分來自數據生成分布（黑色，虛點線） $p_x$ 與生成分布 $p_g$ （ $G$ ）（綠色，實線）的樣本。下面的水平線是 $z$ 的均勻采樣域。上面的水平線是 $x$ 的域的一部分。向上的箭頭顯示了映射 $x = G (z)$ 如何在變換后的樣本上施加非均勻分布 $p_g$ 。 $G$ 在 $p_g$ 的高密度區域收縮，在低密度區域擴展。 (a) 考慮一個接近收斂的對抗對： $p_g$ 與 $p_{data}$ 相似， $D$ 是一個部分準確的分類器。 (b) 在算法的內循環中， $D$ 被訓練來區分來自數據的樣本，收斂到 $D^*(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$ 。 ? 更新 $G$ 后， $D$ 的梯度引導了 $G (z)$ 流向更有可能被分類為數據的區域。 (d) 經過多次訓練，如果 $G$ 和 $D$ 有足夠的容量，它們將達到一個點，即 $p_g = p_{data}$ 。此時判別器無法區分這兩個分布，即 $\frac{1}{2}$ 。

在實踐中，我們必須使用迭代數值方法來實現游戲。在訓練的內部循環中完全優化 $D$ 在計算上是禁止的，并且在有限的數據集上可能會導致過擬合。相反，我們在優化 $D$ 的k個步驟和優化 $G$ 的一個步驟之間交替。只要 $G$ 的變化足夠緩慢，就能使 $D$ 保持在其最佳解附近。該程序在算法1中正式呈現。

在實踐中，等式1可能不提供足夠的梯度供 $G$ 良好學習。在學習的早期階段，當 $G$ 表現不佳時， $D$ 可以高度自信地拒絕樣本，因為它們與訓練數據明顯不同。在這種情況下， $\log(1 - D(G(z)))$ 會飽和。我們可以訓練 $G$ 來最大化 $\log D(G(z))$ ，而不是訓練 $G$ 來最小化 $\log(1 - D(G(z)))$ 。這個目標函數導致 $G$ 和 $D$ 的動態相同的固定點，但在學習早期提供了更強的梯度。

4 理論結果

生成器 $G$ 隱式地定義了一個概率分布 $p_g$ ，當 $\sim p_z$ 時，這個分布作為樣本 $G (z)$ 的分布。因此，如果給定足夠的容量和訓練時間，我們希望算法1收斂到 $p_{data}$ 的一個良好估計器。本節的結果是在一個非參數設置中完成的，例如，我們通過研究概率密度函數空間中的收斂來表示具有無限容量的模型。

算法 1 用于GAN的小批量隨機梯度下降訓練。應用于判別器的步驟數， $k$ ，是一個超參數。在我們的實驗中，我們使用了 $k = 1$ ，這是最不昂貴的選項。

for number of training iterations do

for k steps do

從噪聲先驗 $p_g(z)$ 中抽樣m個噪聲樣本 $\{z^{(1)}, \ldots, z^{(m)}\}$ 。
從數據生成分布 $p_{data}(x)$ 中抽樣m個樣本 $\{x^{(1)}, \ldots, x^{(m)}\}$ 。
通過提升其隨機梯度來更新判別器:

$\nabla \theta_d \frac{1}{m} \sum_{i=1}^{m} \left[ \log D \left( x^{(i)} \right) + \log \left( 1 - D \left( G \left( z^{(i)} \right) \right) \right) \right]$

end for

從噪聲先驗 $p_g(z)$ 中抽樣m個噪聲樣本 $\{z^{(1)}, \ldots, z^{(m)}\}$ 。

通過降低其隨機梯度來更新生成器:

$\nabla \theta_g \frac{1}{m} \sum_{i=1}^{m} \log \left( 1 - D \left( G \left( z^{(i)} \right) \right) \right)$

end for

基于梯度的更新可以使用任何標準的基于梯度的學習規則。我們在我們的實驗中使用了動量。

4.1 $p_g = p_{data}$ 的全局最優性

我們首先考慮任何給定生成器 $G$ 的最優判別器 $D$ 。

命題 1 對于固定的 $G$ ，最優判別器 $D$ 為
$D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} \tag{2}$

證明：給定任何生成器 $G$ ，判別器 $D$ 的訓練標準是最大化量 $V (G, D)$

$\begin{align} V(G, D) & = \int_x p_{data}(x) \log(D(x))dx + \int_z p_z(z) \log(1 - D(g(z)))dz \\ & = \int_x p_{data}(x) \log(D(x)) + p_g(x) \log(1 - D(x))dx \end{align} \tag{3}$

對于任何 $\in \mathbb{R}^2 \setminus \{0, 0\}$ ，函數 $\rightarrow a \log(y) + b \log(1 - y)$ 在 $[0, 1]$ 中達到其最大值，即 $\frac{a}{a+b}$ 。判別器不需要在 $Supp(p_{data}) \cup Supp(p_g)$ 之外定義，從而得出證明。

請注意， $D$ 的訓練目標可以解釋為最大化對條件概率 $P (Y = y ∣ x)$ 的對數似然估計，其中 $Y$ 表示 $x$ 是否來自 $p_{data}$ （當 $y = 1$ 時）或來自 $p_g$ （當 $y = 0$ 時）。現在，方程1中的極小極大游戲可以重新表述為：

$\begin{align} C(G) & = \max_{D} V (G, D) \\ & = \mathbb{E}_{x\sim p_{data}} [\log D^*_{G}(x)] + \mathbb{E}_{z\sim p_z} [\log(1 - D^*_{G}(G(z)))] \\ & = \mathbb{E}_{x\sim p_{data}} [\log D^*_{G}(x)] + \mathbb{E}_{x\sim p_g} [\log(1 - D^*_{G}(x))] \\ & = \mathbb{E}_{x\sim p_{data}} \left[ \log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} \right] + \mathbb{E}_{x\sim p_g} \left[ \log \frac{p_g(x)}{p_{data}(x) + p_g(x)} \right] \end{align} \tag{4}$

定理 1 當且僅當 $p_g = p_{data}$ 時，虛擬訓練準則 $C (G)$ 達到全局最小值。在那一點上， $C (G)$ 達到值 $\log 4$ 。

證明：對于 $p_g = p_{data}$ ， $D^*_G(x) = \frac{1}{2}$ （參考方程2）。因此，通過在 $D^*_G(x) = \frac{1}{2}$ 時檢查方程4，我們發現 $\log \frac{1}{2} + \log \frac{1}{2} = - \log 4$ 。要看到這是 $C (G)$ 的最佳可能值，只有在 $p_g = p_{data}$ 時才能達到，請注意

$\mathbb{E}_{x\sim p_{data}} [- \log 2] + \mathbb{E}_{x\sim p_g} [- \log 2] = - \log 4$

并且通過從 $C(G) = V (D^*_G, G)$ 中減去此表達式，我們得到：

$\log(4) + \text{KL} \left( p_{data} \middle| \middle| \frac{p_{data} + p_g}{2} \right) + \text{KL} \left( p_g \middle| \middle| \frac{p_{data} + p_g}{2} \right) \tag{5}$

其中 KL 是 Kullback–Leibler 散度。我們在上述表達式中識別出模型分布與數據生成過程之間的 Jensen–Shannon 散度：

$\log(4) + 2 \cdot \text{JSD} (p_{data} \parallel p_g) \tag{6}$

由于兩個分布之間的 Jensen–Shannon 散度總是非負的，并且僅當它們相等時為零，我們已經證明了 $C^* = - \log(4)$ 是 $C (G)$ 的全局最小值，唯一的解是 $p_g = p_{data}$ ，即生成模型完美復制了數據生成過程。

4.2 算法1的收斂性

命題2 如果 $G$ 和 $D$ 有足夠的容量，并且在算法1的每一步中，都允許鑒別器 $D$ 在給定 $G$ 的情況下達到其最優，并且 $p_g$ 被更新以改善準則
$\mathbb{E}_{x\sim p_{data}} [\log D^*_{G}(x)] + \mathbb{E}_{x\sim p_g} [\log(1 - D^*_{G}(G(x)))]$

那么 $p_g$ 收斂于 $p_{data}$

證明：考慮 $V(G, D) = U(p_g, D)$ 作為 $p_g$ 的函數，如上述準則所做的那樣。注意 $U(p_g, D)$ 在 $p_g$ 中是凸的。凸函數的最大值的次導數包括在最大值取得的點處的函數的導數。換句話說，如果 $\sup_{\alpha\in A} f_\alpha(x)$ 且 $f_\alpha(x)$ 對于每個 $\alpha$ 在 $x$ 中是凸的，那么 $\partial f_\beta(x) \in \partial f$ 如果 $\beta = \arg \sup_{\alpha\in A} f_\alpha(x)$ 。這等效于在給定對應 $G$ 的最優 $D$ 的情況下計算 $p_g$ 的梯度下降更新。 $sup_D U(p_g, D)$ 在 $p_g$ 中是凸的，并且有一個唯一的全局最優值，如定理1所證明的那樣，因此，通過對 $p_g$ 進行足夠小的更新， $p_g$ 收斂于 $p_x$ ，從而得出證明。

實際上，對抗網絡通過函數 $\theta_g)$ 表示 $p_g$ 分布的有限族，并且我們優化 $\theta_g$ 而不是 $p_g$ 本身。使用多層感知機定義 $G$ 會在參數空間中引入多個臨界點。然而，多層感知機在實踐中的出色性能表明，盡管缺乏理論保證，它們仍是合理的模型。

5 實驗

我們在一系列數據集上訓練了對抗網絡，包括MNIST[21]，多倫多人臉數據庫(TFD) [27]，和CIFAR-10 [19]。生成器網絡使用了整流線性激活[17,8]和S型激活的混合，而鑒別器網絡則使用了maxout [9]激活。在訓練鑒別器網絡時應用了Dropout[16]。雖然我們的理論框架允許在生成器的中間層使用dropout和其他噪聲，但我們僅將噪聲用作生成器網絡的最底層輸入。

我們通過將高斯Parzen窗擬合到使用 $G$ 生成的樣本，并報告在此分布下的對數似然來估計測試集數據在 $p g$ 下的概率。高斯的σ參數是通過對驗證集進行交叉驗證獲得的。這個程序最初是在Breuleux等人的工作中[7]引入的，并被用于各種精確似然不可行的生成模型[24,3,4]。結果在表1中報告。這種估計似然的方法具有較高的方差，且在高維空間中表現不佳，但據我們所知，這是最好的可用方法。可以采樣但無法直接估計似然的生成模型的進展激發了關于如何評估此類模型的進一步研究。

表 1：基于Parzen窗口的對數似然估計。在MNIST上報告的數字是測試集樣本的平均對數似然，均值的標準誤差是根據樣本計算的。在TFD上，我們根據數據集的折疊計算了標準誤差，并使用每個折疊的驗證集選擇了不同的σ。在TFD上，每個折疊上都進行了σ的交叉驗證，并計算了每個折疊上的平均對數似然。對于MNIST，我們與數據集的實值（而不是二進制）版本的其他模型進行了比較。

在圖2和圖3中，我們展示了訓練后從生成器網絡中抽取的樣本。雖然我們并不聲稱這些樣本優于現有方法生成的樣本，但我們相信這些樣本至少可以與文獻中更好的生成模型相媲美，并突顯了對抗框架的潛力。

圖2：模型樣本的可視化。最右側一列顯示相鄰樣本的最近訓練示例，以證明該模型沒有記憶訓練集。樣本是公平的隨機抽取，沒有精選。與大多數深度生成模型的其他可視化不同，這些圖像顯示了來自模型分布的實際樣本，而不是隱藏單元樣本給出的條件均值。此外，這些樣本是不相關的，因為采樣過程不依賴于馬爾可夫鏈混合。a）MNIST b）TFD c）CIFAR-10（全連接模型）d）CIFAR-10（卷積鑒別器和“反卷積”生成器）

圖3：通過在完整模型的z空間坐標之間線性插值獲得的數字。

6 優點和缺點

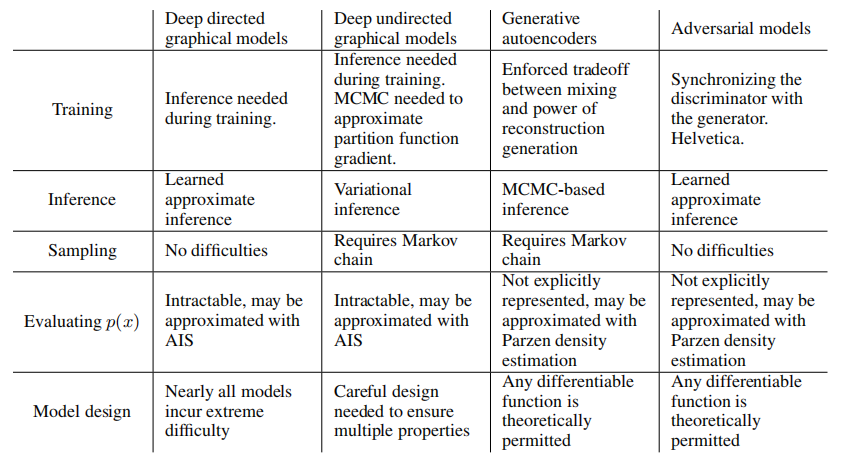
這個新框架相對于先前的建模框架具有優點和缺點。主要的缺點是沒有對 $p g (x)$ 的明確表示，以及訓練過程中 $D$ 必須與 $G$ 很好地同步（特別是，不能在不更新 $D$ 的情況下過度訓練 $G$ ，以避免出現“Helvetica情景”，其中 $G$ 將太多的 $z$ 值塌陷到相同的 $x$ 值，從而沒有足夠的多樣性來模擬 $p_data$ ），就像Boltzmann機器在學習步驟之間必須保持負鏈一樣。優點是永遠不需要Markov鏈，只使用反向傳播來獲得梯度，學習過程中不需要推理，而且可以將各種功能合并到模型中。表2總結了GAN與其他生成建模方法的比較。

表2：生成建模中的挑戰：不同方法在深度生成建模中遇到的主要操作難題的總結。

上述優點主要是計算方面的。敵對模型還可能從生成器網絡不直接用數據示例更新，而只通過通過鑒別器流動的梯度進行更新這一點上獲得一些統計優勢。這意味著輸入的組成部分不會直接復制到生成器的參數中。敵對網絡的另一個優點是，它們可以表示非常銳利，甚至是退化的分布，而基于Markov鏈的方法則要求分布在某種程度上模糊，以便鏈能夠在模式之間混合。

7 結論和未來工作

該框架允許許多直接的擴展：

通過將 $c$ 作為 $G$ 和 $D$ 的輸入，可以獲得條件生成模型 $p (x ∣ c)$ 。
通過訓練一個輔助網絡來預測給定 $x$ 的 $z$ ，可以執行學習近似推斷。這與 wake-sleep 算法[15]訓練的推斷網類似，但具有優勢，即可以在生成網完成訓練后針對固定的生成網訓練推斷網。
可以通過訓練一組共享參數的條件模型，大致地對所有條件 $p(x_S | x_{S_{not}})$ 進行建模，其中 $S$ 是 $x$ 的索引的子集。本質上，可以使用對抗網來實現確定性 MP-DBM [10]的隨機擴展。
半監督學習：當只有有限的標記數據時，來自判別器或推斷網絡的特征可以提高分類器的性能。
效率改進：通過設計更好的方法來協調 $G$ 和 $D$ ，或確定在訓練期間從中采樣 $z$ 的更好分布，可以大大加速訓練。

本文已經展示了對抗建模框架的可行性，表明這些研究方向可能是有用的。

致謝

我們要感謝 Patrice Marcotte、Olivier Delalleau、Kyunghyun Cho、Guillaume Alain 和 Jason Yosinski 為有益的討論。Yann Dauphin 與我們分享了他的 Parzen 窗口評估代碼。我們要感謝 Pylearn2 [11] 和 Theano [6,1] 的開發者，特別是 Frédéric Bastien，他特別為了支持這個項目匆忙推出了一個 Theano 功能。Arnaud Bergeron 在 LATEX 排版方面提供了急需的支持。我們還要感謝 CIFAR 和加拿大研究主席為資助，以及 Compute Canada 和 Calcul Québec 為提供計算資源。Ian Goodfellow 得到了 2013 年 Google Fellowship in Deep Learning 的支持。最后，我們要感謝 Les Trois Brasseurs 刺激了我們的創造力。

參考文獻

Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., Bouchard, N., and Bengio, Y. (2012). Theano: 新功能和速度改進。深度學習和無監督特征學習 NIPS 2012 工作坊。
Bengio, Y. (2009). 學習用于人工智能的深度結構。Now Publishers.
Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013). 通過深度表示改進混合。在 ICML’13 上。
Bengio, Y., Thibodeau-Laufer, E., and Yosinski, J. (2014a). 通過反向傳播訓練的深度生成隨機網絡。在 ICML’14 上。
Bengio, Y., Thibodeau-Laufer, E., Alain, G., and Yosinski, J. (2014b). 通過反向傳播訓練的深度生成隨機網絡。在第30屆國際機器學習大會 (ICML’14) 論文集上。
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010). Theano: 一個 CPU 和 GPU 數學表達式編譯器。在 Python科學計算會議 (SciPy) 論文集上。口頭報告。
Breuleux, O., Bengio, Y., and Vincent, P. (2011). 從 RBM 衍生的過程中快速生成代表性樣本。《神經計算》(Neural Computation)，23(8)，2053–2073。
Glorot, X., Bordes, A., and Bengio, Y. (2011). 深度稀疏整流器神經網絡。在 AISTATS’2011 上。
Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a). 最大輸出網絡。在 ICML’2013 上。
Goodfellow, I. J., Mirza, M., Courville, A., and Bengio, Y. (2013b). 多預測深度 Boltzmann 機。在 NIPS’2013 上。
Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F., and Bengio, Y. (2013c). Pylearn2: 一個機器學習研究庫。arXiv預印本，編號：arXiv:1308.4214。
Gregor, K., Danihelka, I., Mnih, A., Blundell, C., and Wierstra, D. (2014). 深度自回歸網絡。在 ICML’2014 上。
Gutmann, M. and Hyvarinen, A. (2010). 噪聲對比估計：一種新的非規范化統計模型估計方法。在第十三屆國際人工智能和統計學會議 (AISTATS’10) 上。
Hinton, G., Deng, L., Dahl, G. E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P., Sainath, T., and Kingsbury, B. (2012a). 語音識別中的深度神經網絡。《IEEE信號處理雜志》(IEEE Signal Processing Magazine)，29(6)，82–97。
Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). 無監督神經網絡的喚醒-睡眠算法。《科學》(Science)，268，1558–1161。
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2012b). 通過防止特征檢測器的共適應來改進神經網絡。技術報告，編號：arXiv:1207.0580。
Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). 對象識別的最佳多級架構是什么？在國際計算機視覺大會 (ICCV’09) 論文集上，頁碼：2146–2153。IEEE。
Kingma, D. P. and Welling, M. (2014). 自編碼變分貝葉斯。在國際學習表示會議 (ICLR) 論文集上。
Krizhevsky, A. and Hinton, G. (2009). 從小圖像中學習多層特征。技術報告，多倫多大學。
Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). 使用深度卷積神經網絡的ImageNet分類。在 NIPS’2012 上。
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). 基于梯度的文檔識別。《IEEE會議錄》(Proceedings of the IEEE)，86(11)，2278–2324。
Mnih, A. and Gregor, K. (2014). 信念網絡的神經變分推理和學習。技術報告，編號：arXiv:1402.0030。
Rezende, D. J., Mohamed, S., and Wierstra, D. (2014). 深度生成模型中的隨機反向傳播和近似推斷。技術報告，編號：arXiv:1401.4082。
Rifai, S., Bengio, Y., Dauphin, Y., and Vincent, P. (2012). 一種用于采樣收縮自編碼器的生成過程。在 ICML’12 上。
Salakhutdinov, R. and Hinton, G. E. (2009). 深度 Boltzmann 機。在 AISTATS’2009 上，頁碼：448-455。
Schmidhuber, J. (1992). 通過可預測性最小化學習因子碼。《神經計算》(Neural Computation)，4(6)，863–879。
Susskind, J., Anderson, A., and Hinton, G. E. (2010). 多倫多面部數據集。《多倫多大學》技術報告，編號：UTML TR 2010-001。
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I. J., and Fergus, R. (2014). 神經網絡的奇異性質。ICLR，編號：abs/1312.6199。
Tu, Z. (2007). 通過判別方法學習生成模型。在計算機視覺和模式識別，2007年。CVPR’07。IEEE國際會議上，頁碼：1–8。IEEE。

References

Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., Bouchard, N., and Bengio, Y. (2012). Theano: new features and speed improvements. Deep Learning and Unsupervised Feature Learning NIPS 2012 Workshop.
Bengio, Y. (2009). Learning deep architectures for AI. Now Publishers.
Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013). Better mixing via deep representations. In ICML’13.
Bengio, Y., Thibodeau-Laufer, E., and Yosinski, J. (2014a). Deep generative stochastic networks trainable by backprop. In ICML’14.
Bengio, Y., Thibodeau-Laufer, E., Alain, G., and Yosinski, J. (2014b). Deep generative stochastic networks trainable by backprop. In Proceedings of the 30th International Conference on Machine Learning (ICML’14).
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010). Theano: a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy). Oral Presentation.
Breuleux, O., Bengio, Y., and Vincent, P. (2011). Quickly generating representative samples from an RBM-derived process. Neural Computation, 23(8), 2053–2073.
Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse rectifier neural networks. In AISTATS’2011.
Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a). Maxout networks. In ICML’2013.
Goodfellow, I. J., Mirza, M., Courville, A., and Bengio, Y. (2013b). Multi-prediction deep Boltzmann machines. In NIPS’2013.
Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F., and Bengio, Y. (2013c). Pylearn2: a machine learning research library. arXiv preprint arXiv:1308.4214.
Gregor, K., Danihelka, I., Mnih, A., Blundell, C., and Wierstra, D. (2014). Deep autoregressive networks. In ICML’2014.
Gutmann, M. and Hyvarinen, A. (2010). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of The Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS’10).
Hinton, G., Deng, L., Dahl, G. E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P., Sainath, T., and Kingsbury, B. (2012a). Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Processing Magazine, 29(6), 82–97.
Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). The wake-sleep algorithm for unsupervised neural networks. Science, 268, 1558–1161.
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2012b). Improving neural networks by preventing co-adaptation of feature detectors. Technical report, arXiv:1207.0580.
Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). What is the best multi-stage architecture for object recognition? In Proc. International Conference on Computer Vision (ICCV’09), pages 2146–2153. IEEE.
Kingma, D. P. and Welling, M. (2014). Auto-encoding variational bayes. In Proceedings of the International Conference on Learning Representations (ICLR).
Krizhevsky, A. and Hinton, G. (2009). Learning multiple layers of features from tiny images. Technical report, University of Toronto.
Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). ImageNet classification with deep convolutional neural networks. In NIPS’2012.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
Mnih, A. and Gregor, K. (2014). Neural variational inference and learning in belief networks. Technical report, arXiv preprint arXiv:1402.0030.
Rezende, D. J., Mohamed, S., and Wierstra, D. (2014). Stochastic backpropagation and approximate inference in deep generative models. Technical report, arXiv:1401.4082.
Rifai, S., Bengio, Y., Dauphin, Y., and Vincent, P. (2012). A generative process for sampling contractive auto-encoders. In ICML’12.
Salakhutdinov, R. and Hinton, G. E. (2009). Deep Boltzmann machines. In AISTATS’2009, pages 448455.
Schmidhuber, J. (1992). Learning factorial codes by predictability minimization. Neural Computation, 4(6), 863–879.
Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTML TR 2010-001, U. Toronto.
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I. J., and Fergus, R. (2014). Intriguing properties of neural networks. ICLR, abs/1312.6199.
er, J. (1992). Learning factorial codes by predictability minimization. Neural Computation, 4(6), 863–879.
Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTML TR 2010-001, U. Toronto.
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I. J., and Fergus, R. (2014). Intriguing properties of neural networks. ICLR, abs/1312.6199.
Tu, Z. (2007). Learning generative models via discriminative approaches. In Computer Vision and Pattern Recognition, 2007. CVPR’07. IEEE Conference on, pages 1–8. IEEE.