目錄
1 表達圖元的方法
1.1 隱式表示法
1.2 參數表示
1.3 直接表示
2. 直線和射線
2.1 射線的不同表示法
2.1.1 兩點表示
2.1.2 參數表示
2.1.3 相互轉換
?2.2 直線的不同表示法
2.2.1 隱式表示法
2.2.2 斜截式
2.2.3 相互轉換
3. 球
3.1 隱式表示
?
1 表達圖元的方法
1.1 隱式表示法
定義一個布爾函數f(x,y,z),點在圖元上,則布爾函數為真,否則為假。例如
??
1.2 參數表示
t從0-1變化,點(x(t), y(t))的軌跡就是所描述的圖元,上面描述的是中心在原點的單位圓。
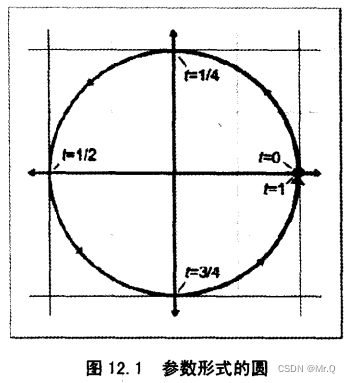
?t有時的變換范圍是0-L,L是圖元的長度。上面的函數只有一個參數,是單變量,其軌跡是一個曲線,如果是兩個變量,其軌跡是曲面。
1.3 直接表示
直接體現圖元的本質信息。例如線段:兩個端點表示;球:球心和半徑表示。
2. 直線和射線
經典定義

?書中對射線定義做了修改:有向線段。

2.1 射線的不同表示法
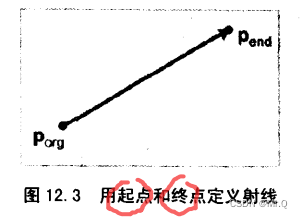
2.1.1 兩點表示
兩個端點p_org和p_end
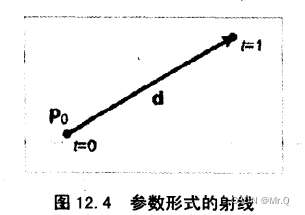
2.1.2 參數表示
或者
起點坐標是p(0)=p_0, 終點坐標是p(1)=p_0 + d,p_0 (即p_org)指定了了射線的位置信息,向量d指定了長度和方向(d = p_end - p_org = (dx, dy))。
2.1.3 相互轉換
兩點形式 -> 參數形式?
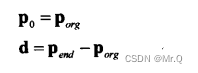
?參數形式 -> 兩點形式
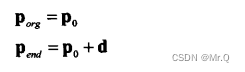
?2.2 直線的不同表示法
2.2.1 隱式表示法

?記向量n=[a, b], p是線上任意一點,d是標量,則向量記法的隱式表示法

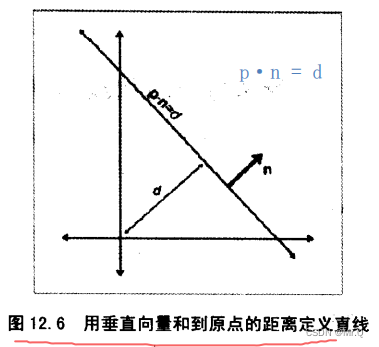
其中向量n轉換成單位向量:
?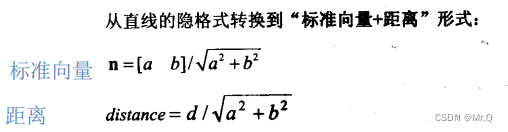
?
?轉換:射線( d = (dx, dy), p_org = (p_orgx, p_orgy) )所在的隱式表示直線
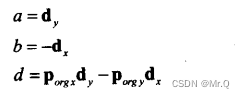
2.2.2 斜截式
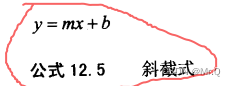
?

2.2.3 相互轉換
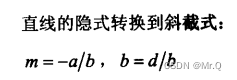
其中隱式ax+by=d, 令x=0,則截距y=d/b.
3. 球
3.1 隱式表示

?到球心c的距離為給定距離r的點的集合,p為球面上點。隱式表示:
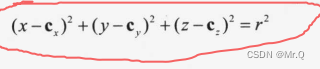
?

)
模塊使用教程)




![[國產MCU]-BL602開發實例-I2C與總線設備地址掃描](http://pic.xiahunao.cn/[國產MCU]-BL602開發實例-I2C與總線設備地址掃描)



九:自定義組件封裝下)


)




】)