群體智能
鳥群:

魚群:

1.基本介紹
蟻群算法(Ant Colony Optimization, ACO)是一種模擬自然界螞蟻覓食行為的優化算法。它通常用于解決路徑優化問題,如旅行商問題(TSP)。
蟻群算法的基本步驟
初始化:設置螞蟻數量、信息素重要程度、啟發因子重要程度、信息素的揮發速率和信息素的初始量。
構建解:每只螞蟻根據概率選擇下一個城市,直到完成一次完整的路徑。
更新信息素:在每條路徑上更新信息素,通常新的信息素量與路徑的質量成正比。
迭代:重復構建解和更新信息素的步驟,直到達到預設的迭代次數。
2.公式化蟻群算法
-
轉移概率 P i j k P_{ij}^k Pijk? 表示螞蟻 k k k從城市 i i i轉移到城市 j j j的概率。它是基于信息素強度 τ i j \tau_{ij} τij?(信息素重要程度為 α \alpha α和啟發式信息 η i j \eta_{ij} ηij?)(啟發式信息重要程度為 β \beta β )計算的:
P i j k = [ τ i j ] α ? [ η i j ] β ∑ l ∈ allowed k [ τ i l ] α ? [ η i l ] β P_{ij}^k = \frac{[\tau_{ij}]^\alpha \cdot [\eta_{ij}]^\beta}{\sum_{l \in \text{allowed}_k} [\tau_{il}]^\alpha \cdot [\eta_{il}]^\beta} Pijk?=∑l∈allowedk??[τil?]α?[ηil?]β[τij?]α?[ηij?]β?
其中, allowed k \text{allowed}_k allowedk? 是螞蟻 k k k 可以選擇的下一個城市集合。
-
信息素更新規則。在每次迭代結束后,所有路徑上的信息素會更新。更新規則通常包括信息素的揮發和信息素的沉積:
τ i j ← ( 1 ? ρ ) ? τ i j + Δ τ i j \tau_{ij} \leftarrow (1 - \rho) \cdot \tau_{ij} + \Delta \tau_{ij} τij?←(1?ρ)?τij?+Δτij?
其中,( ρ \rho ρ ) 是信息素的揮發率,( Δ τ i j \Delta \tau_{ij} Δτij? ) 是本次迭代中所有螞蟻在路徑 ( i , j ) (i, j) (i,j) 上留下的信息素總量,通常計算方式為_
Δ τ i j = ∑ k = 1 m Δ τ i j k \Delta \tau_{ij} = \sum_{k=1}^{m} \Delta \tau_{ij}^k Δτij?=∑k=1m?Δτijk?
而對于每只螞蟻 k k k ,在路徑 ( i , j ) (i, j) (i,j) 上留下的信息素量 Δ τ i j k \Delta \tau_{ij}^k Δτijk? 通常與其走過的路徑長度成反比:
Δ τ i j k = { Q L k , if?ant? k travels?on?edge? ( i , j ) 0 , otherwise \Delta \tau_{ij}^k= \begin{cases} \frac{Q}{L_k}, & \text{if ant } k \text{ travels on edge } (i, j) \\ 0, & \text{otherwise} \end{cases} Δτijk?={Lk?Q?,0,?if?ant?k?travels?on?edge?(i,j)otherwise?
這里, Q Q Q是一個常數, L k L_k Lk?是螞蟻 k k k的路徑長度。
-
啟發式信息 ( η i j \eta_{ij} ηij? ) 通常是目標函數的倒數,例如在TSP問題中,它可以是兩城市間距離的倒數:
η i j = 1 d i j \eta_{ij} = \frac{1}{d_{ij}} ηij?=dij?1?
其中, d i j d_{ij} dij? 是城市 i i i和 j j j 之間的距離。
這些公式構成了蟻群算法的數學基礎。通過調整參數 α \alpha α , β \beta β, 和 ρ \rho ρ,可以控制算法的搜索行為,從而適應不同的優化問題。
3.代碼實現
import numpy as np
import matplotlib.pyplot as pltclass AntColonyOptimizer:def __init__(self, distances, n_ants, n_best, n_iterations, decay, alpha=1, beta=1):# 初始化參數self.distances = distances # 城市間的距離矩陣self.pheromone = np.ones(self.distances.shape) / len(distances) # 初始化信息素矩陣self.all_inds = range(len(distances)) # 所有城市的索引self.n_ants = n_ants # 螞蟻數量self.n_best = n_best # 每輪保留的最佳路徑數self.n_iterations = n_iterations # 迭代次數self.decay = decay # 信息素的揮發率self.alpha = alpha # 信息素重要程度self.beta = beta # 啟發因子的重要程度def run(self):# 運行算法shortest_path = Noneshortest_path_length = float('inf')for iteration in range(self.n_iterations): # 對每次迭代all_paths = self.gen_all_paths() # 生成所有螞蟻的路徑self.spread_pheromone(all_paths, self.n_best, shortest_path_length) # 更新信息素shortest_path, shortest_path_length = self.find_shortest_path(all_paths) # 找到最短路徑self.plot_paths(shortest_path, iteration, shortest_path_length) # 繪制路徑return shortest_path, shortest_path_lengthdef gen_path_dist(self, path):# 計算路徑長度total_dist = 0for i in range(len(path) - 1):total_dist += self.distances[path[i], path[i+1]]return total_distdef gen_all_paths(self):# 生成所有螞蟻的路徑all_paths = []for _ in range(self.n_ants):path = [np.random.randint(len(self.distances))] # 選擇一個隨機起點while len(path) < len(self.distances):move_probs = self.gen_move_probs(path) # 生成移動概率next_city = np_choice(self.all_inds, 1, p=move_probs)[0] # 選擇下一個城市path.append(next_city)all_paths.append((path, self.gen_path_dist(path))) # 添加路徑和長度return all_pathsdef spread_pheromone(self, all_paths, n_best, shortest_path_length):# 更新信息素sorted_paths = sorted(all_paths, key=lambda x: x[1]) # 按路徑長度排序for path, dist in sorted_paths[:n_best]: # 只取最好的n_best條路徑for i in range(len(path) - 1):self.pheromone[path[i], path[i+1]] += 1.0 / self.distances[path[i], path[i+1]]def find_shortest_path(self, all_paths):# 尋找最短路徑shortest_path = min(all_paths, key=lambda x: x[1]) # 根據路徑長度找到最短的那條return shortest_path[0], shortest_path[1]def gen_move_probs(self, path):# 生成移動概率last_city = path[-1]probs = np.zeros(len(self.distances))for i in self.all_inds:if i not in path:pheromone = self.pheromone[last_city, i] ** self.alphaheuristic = (1.0 / self.distances[last_city, i]) ** self.betaprobs[i] = pheromone * heuristicreturn probs / probs.sum()def plot_paths(self, best_path, iteration, path_length):# 繪制路徑plt.figure(figsize=(10, 6))for i in range(len(coords)): # 繪制所有可能的路徑for j in range(i+1, len(coords)):plt.plot([coords[i][0], coords[j][0]], [coords[i][1], coords[j][1]], 'k:', alpha=0.5)for i in range(len(best_path) - 1): # 繪制最短路徑start_city = best_path[i]end_city = best_path[i+1]plt.plot([coords[start_city][0], coords[end_city][0]], [coords[start_city][1], coords[end_city][1]], 'b-', linewidth=2)plt.scatter(*zip(*coords), color='red') # 標記城市位置for i, coord in enumerate(coords): # 添加城市標簽plt.text(coord[0], coord[1], str(i), color='green')plt.title(f'Iteration: {iteration}, Shortest Path Length: {round(path_length, 2)}')plt.xlabel('X Coordinate')plt.ylabel('Y Coordinate')plt.show()def np_choice(a, size, replace=True, p=None):# numpy的隨機選擇函數return np.array(np.random.choice(a, size=size, replace=replace, p=p))# 城市坐標
coords = np.random.rand(10, 2) # 假設有10個城市# 計算距離矩陣
distances = np.zeros((10, 10))
for i in range(10):for j in range(10):distances[i, j] = np.linalg.norm(coords[i] - coords[j]) # 使用歐幾里得距離# 運行蟻群算法
aco = AntColonyOptimizer(distances, n_ants=10, n_best=5, n_iterations=100, decay=0.5, alpha=1, beta=2)
path, dist = aco.run()執行結果:


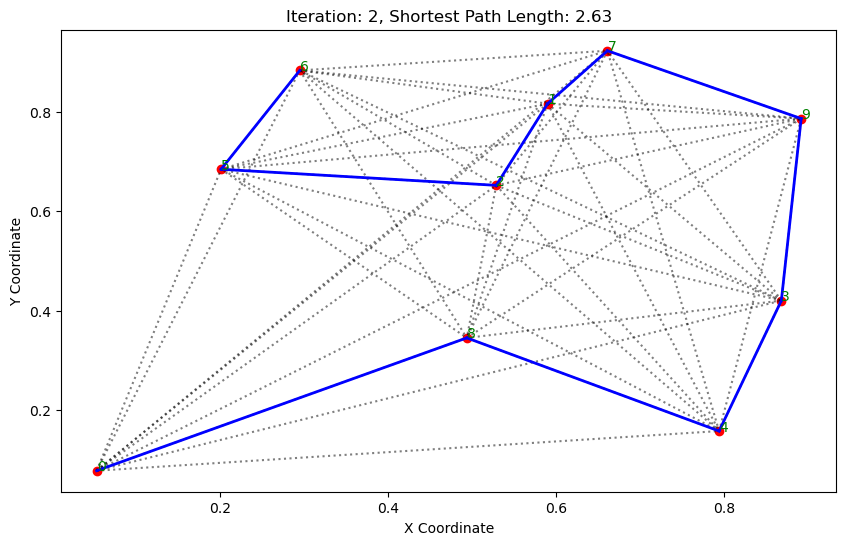
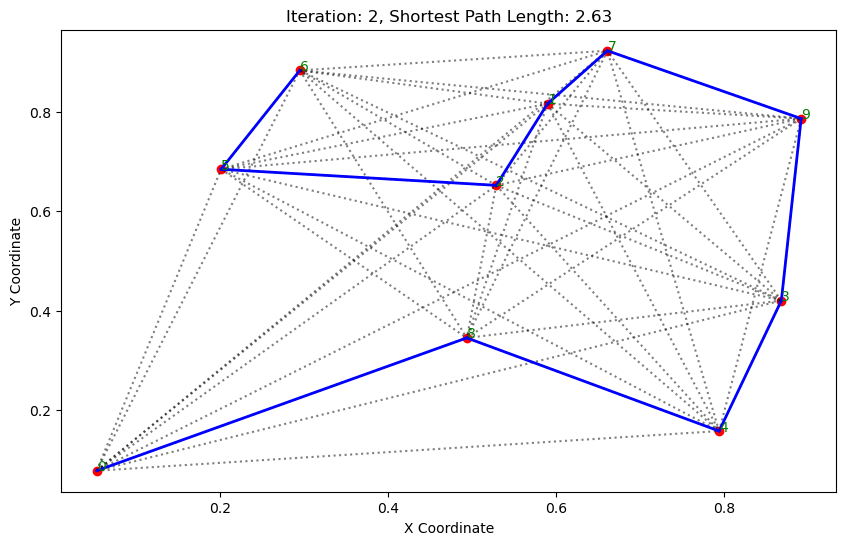
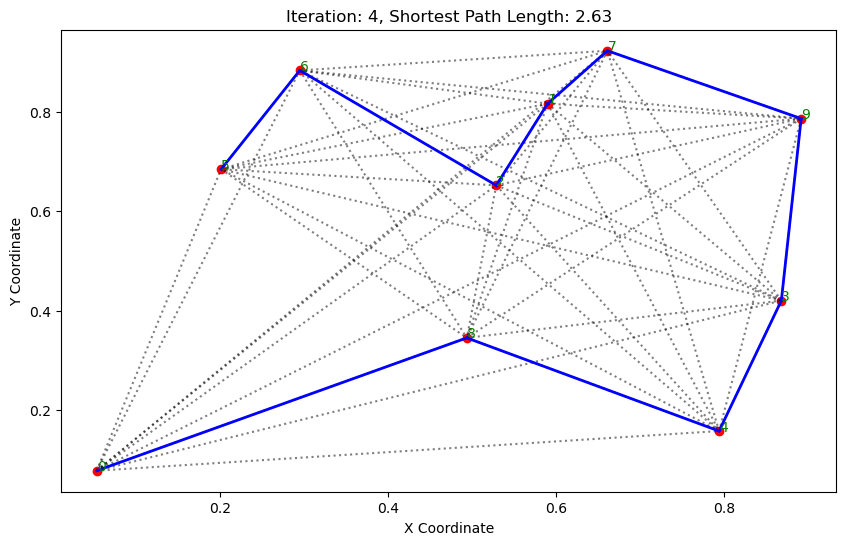
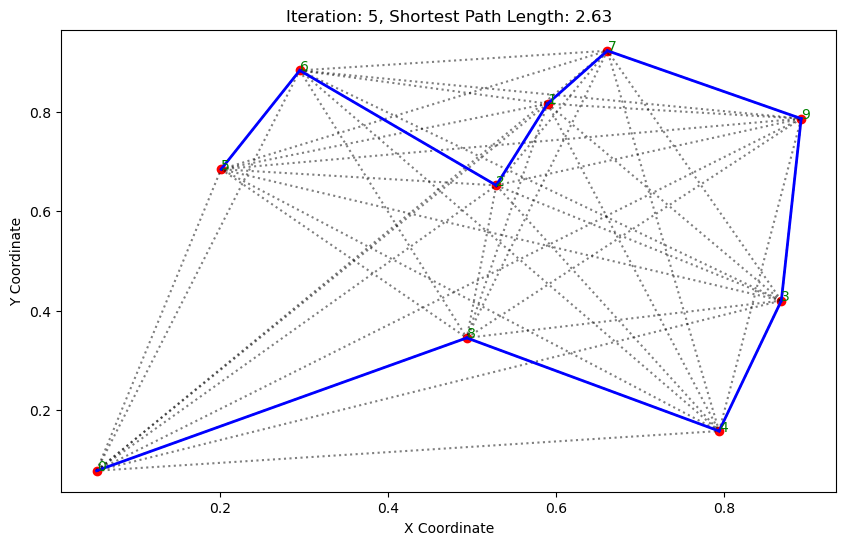
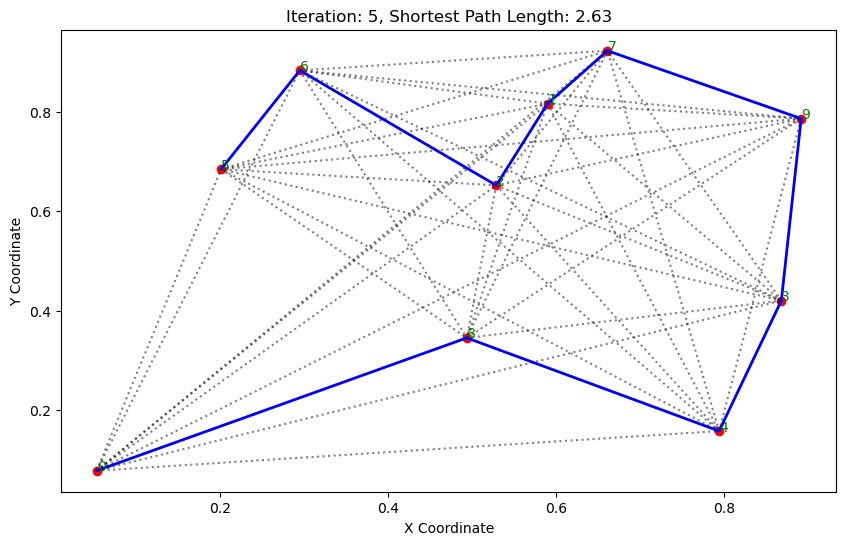
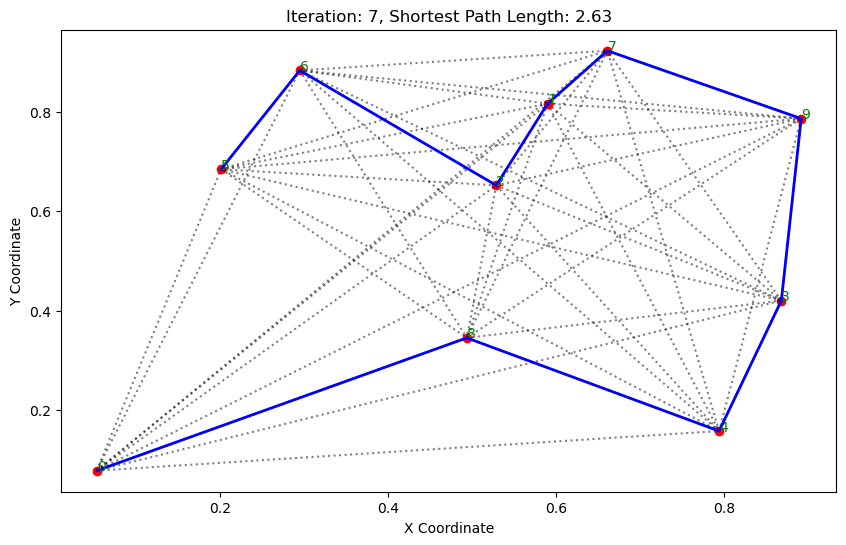
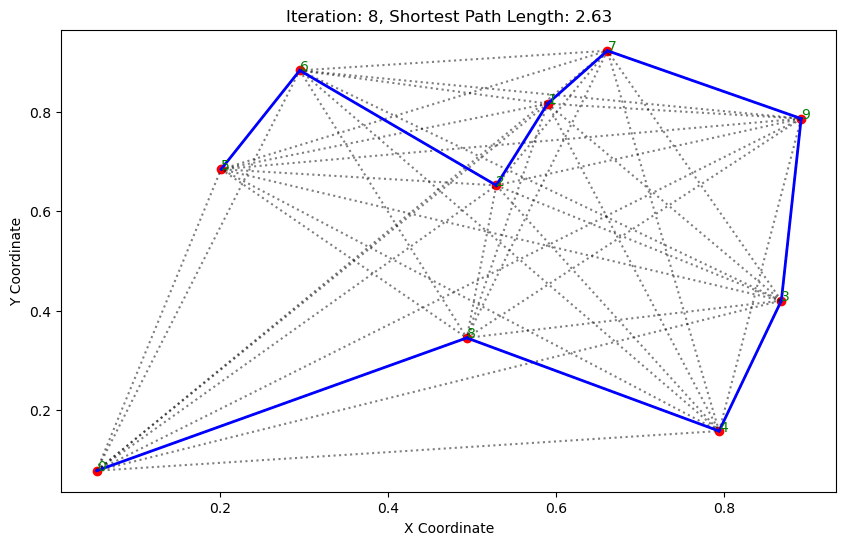
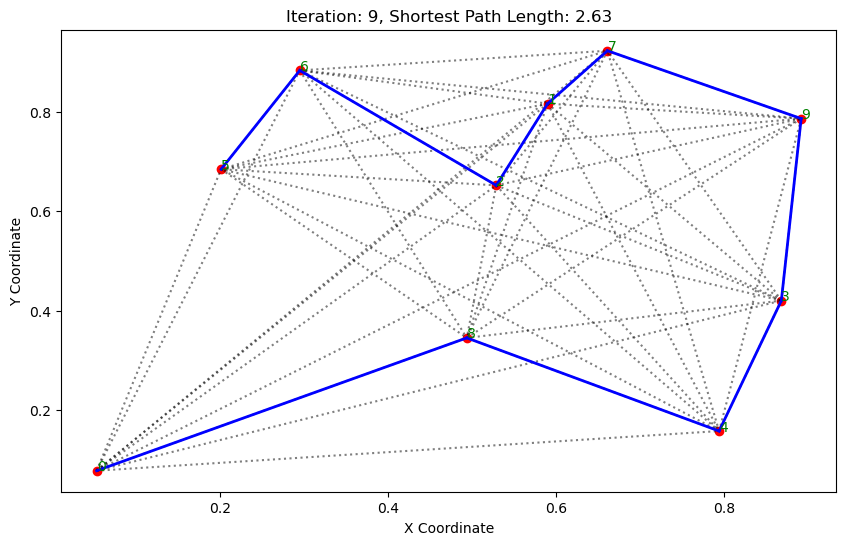
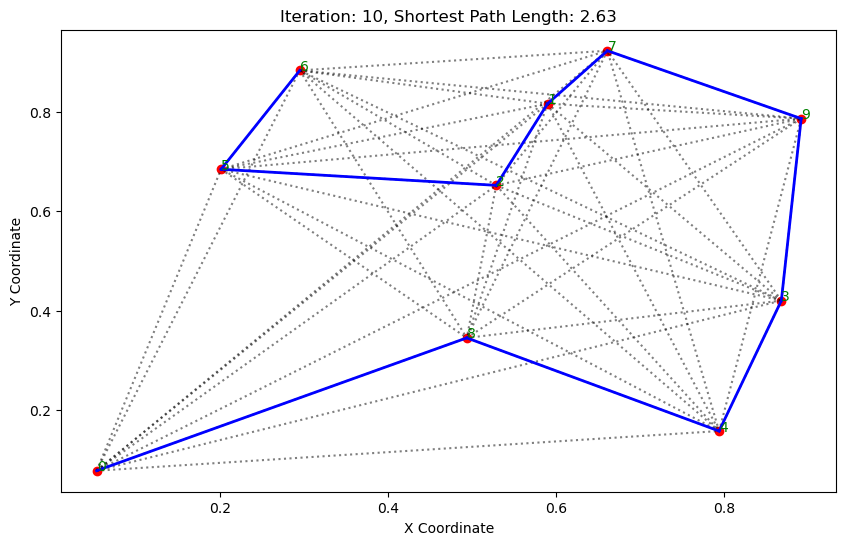
. . . . . . ...... ......
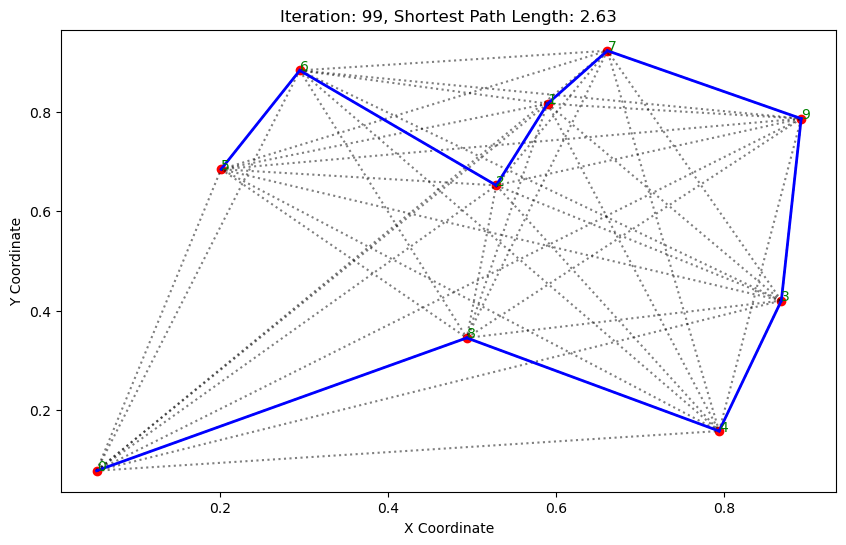






![bzoj 1996: [Hnoi2010]chorus 合唱隊](http://pic.xiahunao.cn/bzoj 1996: [Hnoi2010]chorus 合唱隊)

)






)


)
