題目

對于給定的整數 n, 如果n的k（k>=2）進制數的所有數位全為1，則稱 k（k>=2）是 n 的一個好進制。

以字符串的形式給出 n, 以字符串的形式返回 n 的最小好進制。

• 示例 1：

輸入：“13”
輸出：“3”
解釋：13 的 3 進制是 111。

• 示例 2：

輸入：“4681”
輸出：“8”
解釋：4681 的 8 進制是 11111。

• 示例 3：

輸入：“1000000000000000000”
輸出：“999999999999999999”
解釋：1000000000000000000 的 999999999999999999 進制是 11。

提示：

• n的取值范圍是 [3, 10^18]。
• 輸入總是有效且沒有前導 0。

等比數列求和

如果n的k（k>=2）進制數的所有數位全為1，那么可以表示為一個等比數列相加

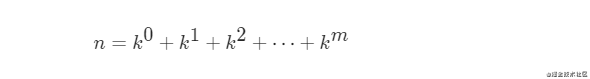
因此根據等比數列求和公式可得

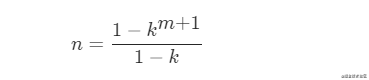
變形得：

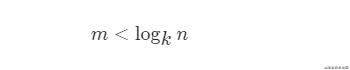
因為n的取值范圍是 [3, 10^18]并且k>=2,根據log函數的單調性可得:m<60

二項式定理

根據二項式定理可得

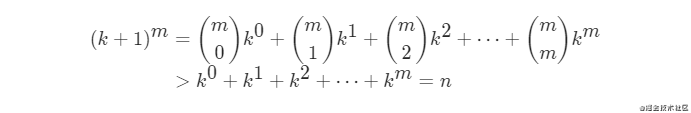
又因為

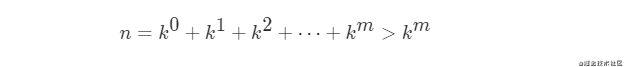
二式結合可得

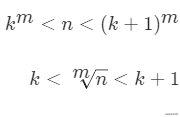
最終可求得k

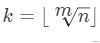
解題思路

1. 根據等比數列求和，我們可以快速得到m的最大值，從而縮小我們的搜索范圍

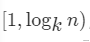
2. 根據上一步得出的m的取值范圍進行遍歷，通過二項式定理得出的結論

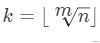
可以求出k值，再檢驗當前k值能否組成n

代碼

class Solution {public String smallestGoodBase(String n) {long num = Long.parseLong(n);int maxL = (int) Math.floor(Math.log(num) / Math.log(2));for (int m=maxL;m>1;m--){int k = (int) Math.pow(num, 1.0 / m);long cur=1,pow=1;for(int i=0;i<m;i++){pow*=k;cur+=pow;}if(cur==num)return String.valueOf(k);}return String.valueOf(num-1);}
}