2017. 網格游戲

給你一個下標從 0 開始的二維數組 grid ，數組大小為 2 x n ，其中 grid[r][c] 表示矩陣中 (r, c) 位置上的點數。現在有兩個機器人正在矩陣上參與一場游戲。

兩個機器人初始位置都是 (0, 0) ，目標位置是 (1, n-1) 。每個機器人只會 向右 ((r, c) 到 (r, c + 1)) 或 向下 ((r, c) 到 (r + 1, c)) 。

游戲開始，第一個 機器人從 (0, 0) 移動到 (1, n-1) ，并收集路徑上單元格的全部點數。對于路徑上所有單元格 (r, c) ，途經后 grid[r][c] 會重置為 0 。然后，第二個 機器人從 (0, 0) 移動到 (1, n-1) ，同樣收集路徑上單元的全部點數。注意，它們的路徑可能會存在相交的部分。

第一個 機器人想要打擊競爭對手，使 第二個 機器人收集到的點數 最小化 。與此相對，第二個 機器人想要 最大化 自己收集到的點數。兩個機器人都發揮出自己的 最佳水平 的前提下，返回 第二個 機器人收集到的 點數 。

示例 1：

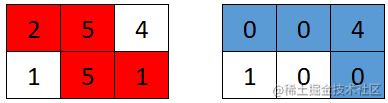
輸入：grid = [[2,5,4],[1,5,1]]
輸出：4
解釋：第一個機器人的最佳路徑如紅色所示，第二個機器人的最佳路徑如藍色所示。
第一個機器人訪問過的單元格將會重置為 0 。
第二個機器人將會收集到 0 + 0 + 4 + 0 = 4 個點。

示例 2：

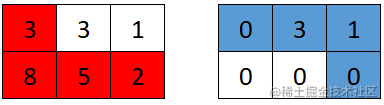
輸入：grid = [[3,3,1],[8,5,2]]
輸出：4
解釋：第一個機器人的最佳路徑如紅色所示，第二個機器人的最佳路徑如藍色所示。 
第一個機器人訪問過的單元格將會重置為 0 。
第二個機器人將會收集到 0 + 3 + 1 + 0 = 4 個點。

示例 3：

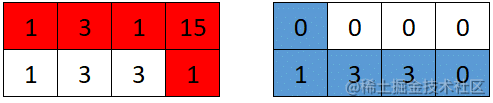
輸入：grid = [[1,3,1,15],[1,3,3,1]]
輸出：7
解釋：第一個機器人的最佳路徑如紅色所示，第二個機器人的最佳路徑如藍色所示。
第一個機器人訪問過的單元格將會重置為 0 。
第二個機器人將會收集到 0 + 1 + 3 + 3 + 0 = 7 個點。

提示：

grid.length == 2
n == grid[r].length
1 <= n <= 5 * 104
1 <= grid[r][c] <= 105

解題思路

以示例一為例子

通過觀察可得，只要機器人一選出了任意一條路徑，那么機器人二無論如何最多只能收集第一行或者第二行中，未被置為0的那部分點數。例如示例一，機器人二無論走什么路徑，最多只能收集第一行的點數總和4或者第二行的點數總和1.因此，我們可以嘗試全部機器人一的路徑，但是因為我們只是關心第一行和第二行置為0以后的點數，因此可以使用前綴和，快速得出，每一行置為0以后的剩余點數，機器人二就會選擇剩余點數多的那行進行收集，而我們的目的就是找出使得機器人二收集最少點數的路徑

代碼

class Solution {
public:long long gridGame(vector<vector<int>> grid) {int n=grid[0].size();vector<long long > pre1(n),pre2(n);pre1[0]=grid[0][0];pre2[0]=grid[1][0];for (int i = 1; i < n; ++i) {pre1[i]=pre1[i-1]+grid[0][i];pre2[i]=pre2[i-1]+grid[1][i];}long long s1=pre1[n-1],s2=pre2[n-1];long long m=s1-pre1[0];for (int i = 1; i < n; ++i) {m=min(m,max(s1-pre1[i],pre2[i-1]));}return m;}
};