你在這里 (You are here)

If you’re reading this, odds are: (1) you’re interested in bayesian statistics but (2) you have no idea how Markov Chain Monte Carlo (MCMC) sampling methods work, and (3) you realize that all but the simplest, toy problems require MCMC sampling so you’re a bit unsure of how to move forward.

如果您正在閱讀此書，則可能是：(1)您對貝葉斯統計感興趣，但(2)您不知道馬爾可夫鏈蒙特卡洛(MCMC)采樣方法的工作原理，以及(3)您意識到，除了最簡單的玩具問題需要MCMC采樣，因此您不確定如何前進。

Not to worry, we’ll explore this tricky concept using a 1-dimensional normal distribution, using nothing more than python, user-defined functions, and the random module (specifically, the uniform distribution.) We’ll discuss all this nonsense in terms of bars, beers, and a night out with your pals.

不用擔心，我們將使用一維正態分布探索這個棘手的概念，僅使用python，用戶定義函數和隨機模塊(特別是統一分布)。我們將在下面討論所有這些廢話。酒吧，啤酒和與朋友共度夜晚的條件

在酒吧想象自己 (Picture yourself at a bar)

It’s Friday night, you and your gang head out for burgers, beer and to catch a televised baseball game. Let’s say you arbitrarily pick a first bar (we’ll call it Larry’s Sports Bar), you sit down, grab a menu and consider your options. If the food and drinks are affordable, that’s a good reason to stay; but if there’s standing room only, you’ve got a reason to leave. If the bar’s filled with big screen TVs all dialed into the right game, another reason to stay. If the food or drinks aren’t appealing, you’ve got another reason to leave. Etc etc, you get the point.

這是星期五晚上，您和幫派前往漢堡，啤酒和觀看電視轉播的棒球比賽。 假設您隨意選擇第一個酒吧(我們稱其為Larry's Sports Bar )，您坐下來，拿起一個菜單并考慮您的選擇。 如果食物和飲料負擔得起，那就是留下的充分理由。 但是如果只有客廳，那您就有理由離開。 如果酒吧的大屏幕電視都播放了正確的游戲，這是留下的另一個原因。 如果食物或飲料不受歡迎，您還有其他理由離開。 等等，您明白了。

Now, let’s say one (or several) of your friends have gripes with the current establishment — the food is cold, the beers are overpriced, whatever the reason. So he proposes the gang leave Larry’s Sports Bar in favor of Tony’s Pizzeria and Beer Garden because the food there is better, fresher, etc. So the gang deliberates, asking the questions (A) how favorable is Larry’s? (B) How favorable is Tony’s? And (C) how favorable is Tony’s relative to Larry’s?

現在，比方說，您的一個(或幾個)朋友對當前的餐館感到不快-不管是什么原因，食物都很冷，啤酒價格過高。 因此，他建議該團伙離開拉里的體育館 ，轉而使用托尼的比薩店和啤酒花園，因為那里的食物更好，更新鮮，等等。于是，該團伙在考慮以下問題：(A)拉里一家有多有利？ (B)托尼的優惠程度如何？ (C) 托尼相對于拉里有多有利？

This relative comparison is really the most important detail. If Tony’s is only marginally better than Larry’s (or far worse) there’s a good chance that it’s not worth the effort to relocate. But if Tony’s is unambiguously the better of the two, there’s only a slim chance that you might stay. This is the real juice that makes Metropolis-Hastings “work.”

相對比較確實是最重要的細節。 如果Tony的房屋僅比Larry的房屋略好(或更差)，則很有可能不值得重新安置。 但是，如果托尼(Tony's)無疑是兩者中的佼佼者，那么您留下的可能性很小。 這是使Metropolis-Hastings“工作”的真正汁液 。

算法 (The algorithm)

Metropolis-Hastings algorithm does:

Metropolis-Hastings算法可以：

1. Start with a random sample

   從隨機樣本開始

2. Determine the probability density associated with the sample

   確定與樣本相關的概率密度

3. Propose a new, arbitrary sample (and determine its probability density)

   提出一個新的任意樣本(并確定其概率密度)

4. Compare densities (via division), quantifying the desire to move

   比較密度(通過除法)，量化移動的欲望

5. Generate a random number, compare with desire to move, and decide: move or stay

   生成一個隨機數，與移動的欲望進行比較，并決定：移動還是停留

6. Repeat
   重復

The real key is (as we’ve discussed) quantifying how desirable the move is as an action/inaction criteria, then (new stuff alert!) observe a random event, compare to said threshold, and make a decision.

真正的關鍵是(正如我們已經討論過的那樣)量化移動作為行動/不作為標準的期望程度，然后(新事物警報！) 觀察隨機事件 ，與所述閾值進行比較，然后做出決定。

隨機事件 (The random event)

For our purposes, our threshold is the ratio of the proposed sample’s probability density to the current sample’s probability density. If this threshold is near (or above) 1, it means that the previous location was highly undesirable (a number close to 0, very improbable) and the proposed location is highly desirable (as close to 1 as is possible, near distribution’s expectation). Now, we need to generate a number in the range [0,1] from the uniform distribution. If the number produced is less than or equal to the threshold, we move. Otherwise, we stay. That’s it!

出于我們的目的，我們的閾值是建議樣本的概率密度與當前樣本的概率密度之比。 如果此閾值接近(或高于)1，則意味著先前的位置非常不理想(數字接近0，非常不可能)，建議的位置也非常理想(盡可能接近1，接近分布的期望值) 。 現在，我們需要根據均勻分布生成一個在[0,1]范圍內的數字。 如果產生的數字小于或等于閾值，則移動。 否則，我們留下。 而已！

那硬東西呢？ (What about the hard stuff?)

This is starting to sound a little too good to be true, right? We haven’t discussed Markov Chains or Monte Carlo simulations yet but fret not. Both are huge topics in their own right and we only need the most basic familiarity with each to make use of MCMC magic.

這聽起來似乎太好了，難以置信，對吧？ 我們尚未討論馬爾可夫鏈或蒙特卡洛模擬，但不用擔心。 兩者本身都是很重要的話題，我們只需要對它們有最基本的了解就可以使用MCMC魔術。

A Markov Chain is is a chain of discrete events where the probability of the next event is conditioned only upon the current event. (ex: I just finished studying, do I go to sleep or go to the bar? These are my only choices of a finite set.) In this system of discrete choices, there exists a transition matrix, which quantifies the probability of transitioning from any given state to any given state. A Monte Carlo method is really just a fancy name for a simulation/experiment that relies on usage of random numbers.

馬爾可夫鏈是離散事件的鏈，其中下一個事件的概率僅取決于當前事件。 (例如：我剛剛完成學習，我要去睡覺還是去酒吧？ 這是我對有限集合的唯一選擇。 )在這個離散選擇的系統中，存在一個轉換矩陣，該矩陣量化從任何給定狀態到任何給定狀態。 蒙特卡洛方法實際上只是依賴于隨機數使用的模擬/實驗的奇特名稱。

As discussed, we’ll be sampling from the normal distribution — a continuous, not discrete, distribution. So how can there be a transition matrix? Surprise!— there’s no transition matrix at all. (It’s actually called a Markov kernel, and it’s just the comparison of probability densities, at least for our purposes.)

正如討論的那樣，我們將從正態分布中進行采樣-連續而不是離散的分布。 那么如何有一個過渡矩陣呢？ 驚喜！ —根本沒有過渡矩陣。 (實際上，它被稱為Markov核 ，它只是概率密度的比較，至少出于我們的目的。)

代碼 (The code)

below, we define three functions: (1) Normal, which evaluates the probability density of any observation given the parameters mu and sigma. (2) Random_coin, which references a fellow TDS writer’s post (lined below). And (3) Gaussian_mcmc, which samples executes the algorithm as described above.

下面，我們定義三個函數：(1)正態，在給定參數mu和sigma的情況下評估任何觀測值的概率密度。 (2)Random_coin，它引用了TDS同行作家的帖子(如下所示)。 以及(3)采樣的高斯_mcmc執行上述算法。

As promised, we’re not calling any Gaussian or normal function from numpy, scipy, etc. In the third function, we initialize a current sample as an instance of the uniform distribution (where the lower and upper boundaries are +/- 5 standard deviations from the mean.) Likewise, movement is defined in the same way. Lastly, we move (or stay) based on the random event’s observed value in relation to acceptance, which is the probability density comparison discussed at length elsewhere.

如所承諾的，我們不會從numpy，scipy等中調用任何高斯函數或正態函數。在第三個函數中，我們將當前樣本初始化為均勻分布的實例(上下邊界為+/- 5標準同樣，以相同的方式定義運動。 最后，我們根據與接受相關的隨機事件的觀察值來移動(或停留)，這是在其他地方詳細討論的概率密度比較。

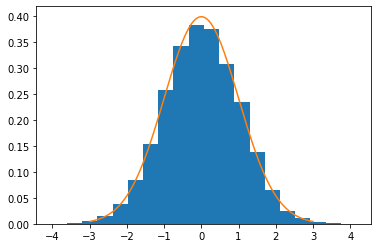
Lastly, one must always give credit where credit is due: Rahul Agarwal’s post defining a Beta distribution MH sampler was instrumental to my development of the above Gaussian distribution MH sampler. I encourage you to read his post as well for a more detailed exploration of the foundational concepts, namely Markov Chains and Monte Carlo simulations.

最后，必須始終在應歸功的地方給予信譽： Rahul Agarwal的職位定義了Beta分布MH采樣器，這對我開發上述高斯分布MH采樣器至關重要。 我鼓勵您也閱讀他的文章，以更詳細地探索基本概念，即馬爾可夫鏈和蒙特卡洛模擬。

Thank you for reading — If you think my content is alright, please subscribe! :)

感謝您的閱讀-如果您認為我的內容還可以，請訂閱！ :)