代碼隨想錄算法訓練營第58天｜動態規劃part15｜392.判斷子序列、115.不同的子序列

392.判斷子序列

392.判斷子序列

思路：

（這道題也可以用雙指針的思路來實現，時間復雜度也是O(n)）

這道題應該算是編輯距離的入門題目，因為從題意中我們也可以發現，只需要計算刪除的情況，不用考慮增加和替換的情況。

所以掌握本題的動態規劃解法是對后面要講解的編輯距離的題目打下基礎。

動態規劃五部曲分析如下：

1. 確定dp數組（dp table）以及下標的含義

dp[i][j] 表示以下標i-1為結尾的字符串s，和以下標j-1為結尾的字符串t，相同子序列的長度為dp[i][j]。

注意這里是判斷s是否為t的子序列。即t的長度是大于等于s的。

2. 確定遞推公式

在確定遞推公式的時候，首先要考慮如下兩種操作，整理如下：

• if (s[i - 1] == t[j - 1])
  t中找到了一個字符在s中也出現了
• if (s[i - 1] != t[j - 1])
  相當于t要刪除元素，繼續匹配

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因為找到了一個相同的字符，相同子序列長度自然要在dp[i-1][j-1]的基礎上加1（如果不理解，在回看一下dp[i][j]的定義）

if (s[i - 1] != t[j - 1])，此時相當于t要刪除元素，t如果把當前元素t[j - 1]刪除，那么dp[i][j] 的數值就是 看s[i - 1]與 t[j - 2]的比較結果了，即：dp[i][j] = dp[i][j - 1];

3. dp數組如何初始化

從遞推公式可以看出dp[i][j]都是依賴于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

這里大家已經可以發現，在定義dp[i][j]含義的時候為什么要表示以下標i-1為結尾的字符串s，和以下標j-1為結尾的字符串t，相同子序列的長度為dp[i][j]。

因為這樣的定義在dp二維矩陣中可以留出初始化的區間，如圖：

如果要是定義的dp[i][j]是以下標i為結尾的字符串s和以下標j為結尾的字符串t，初始化就比較麻煩了。

dp[i][0] 表示以下標i-1為結尾的字符串，與空字符串的相同子序列長度，所以為0. dp[0][j]同理。

vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));

4. 確定遍歷順序

同理從遞推公式可以看出dp[i][j]都是依賴于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍歷順序也應該是從上到下，從左到右

5. 舉例推導dp數組

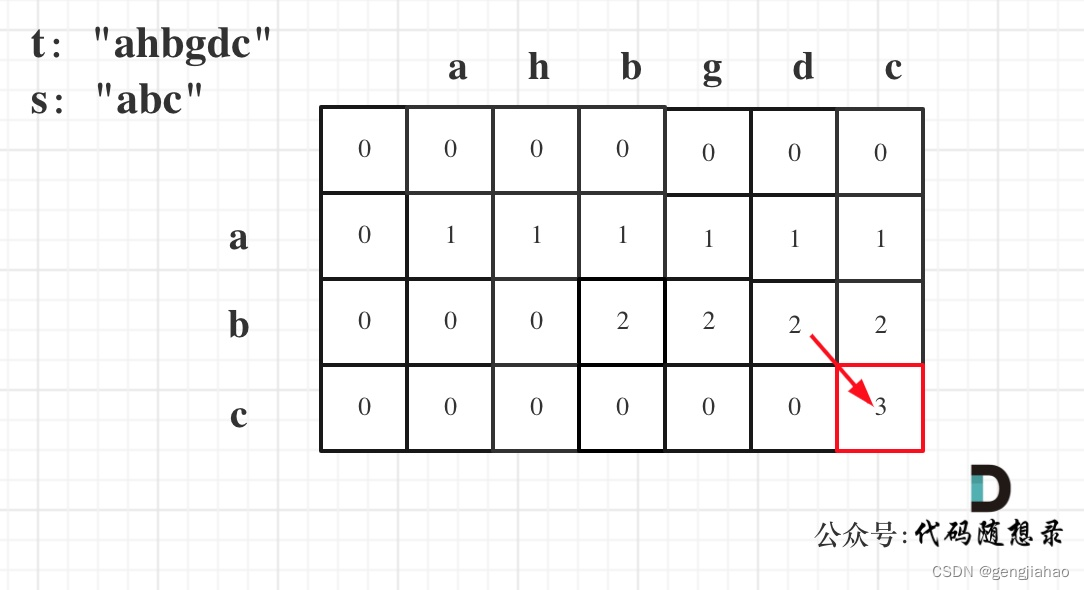
dp[i][j]表示以下標i-1為結尾的字符串s和以下標j-1為結尾的字符串t 相同子序列的長度，所以如果dp[s.size()][t.size()] 與 字符串s的長度相同說明：s與t的最長相同子序列就是s，那么s 就是 t 的子序列。

圖中dp[s.size()][t.size()] = 3， 而s.size() 也為3。所以s是t 的子序列，返回true。

代碼：

python

class Solution(object):def isSubsequence(self, s, t):""":type s: str:type t: str:rtype: bool"""dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = dp[i][j-1]return dp[-1][-1] == len(s)

115.不同的子序列

115.不同的子序列

思路：

動態規劃五部曲：

1. 確定dp數組（dp table）以及下標的含義

dp[i][j]：以i-1為結尾的s子序列中出現以j-1為結尾的t的個數為dp[i][j]。

2. 確定遞推公式

這一類問題，基本是要分析兩種情況

• s[i - 1] 與 t[j - 1]相等
• s[i - 1] 與 t[j - 1] 不相等

當s[i - 1] 與 t[j - 1]相等時，dp[i][j]可以有兩部分組成。

一部分是用s[i - 1]來匹配，那么個數為dp[i - 1][j - 1]。即不需要考慮當前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。

一部分是不用s[i - 1]來匹配，個數為dp[i - 1][j]。

這里可能有錄友不明白了，為什么還要考慮 不用s[i - 1]來匹配，都相同了指定要匹配啊。

所以當s[i - 1] 與 t[j - 1]相等時，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

當s[i - 1] 與 t[j - 1]不相等時，dp[i][j]只有一部分組成，不用s[i - 1]來匹配（就是模擬在s中刪除這個元素），即：dp[i - 1][j]

所以遞推公式為：dp[i][j] = dp[i - 1][j];

3. dp數組如何初始化

從遞推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是從上方和左上方推導而來，如圖：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。

每次當初始化的時候，都要回顧一下dp[i][j]的定義，不要憑感覺初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1為結尾的s可以隨便刪除元素，出現空字符串的個數。

那么dp[i][0]一定都是1，因為也就是把以i-1為結尾的s，刪除所有元素，出現空字符串的個數就是1。

再來看dp[0][j]，dp[0][j]：空字符串s可以隨便刪除元素，出現以j-1為結尾的字符串t的個數。

那么dp[0][j]一定都是0，s如論如何也變成不了t。

最后就要看一個特殊位置了，即：dp[0][0] 應該是多少。

dp[0][0]應該是1，空字符串s，可以刪除0個元素，變成空字符串t。

vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其實這行代碼可以和dp數組初始化的時候放在一起，但我為了凸顯初始化的邏輯，所以還是加上了。

4. 確定遍歷順序

從遞推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根據左上方和正上方推出來的。

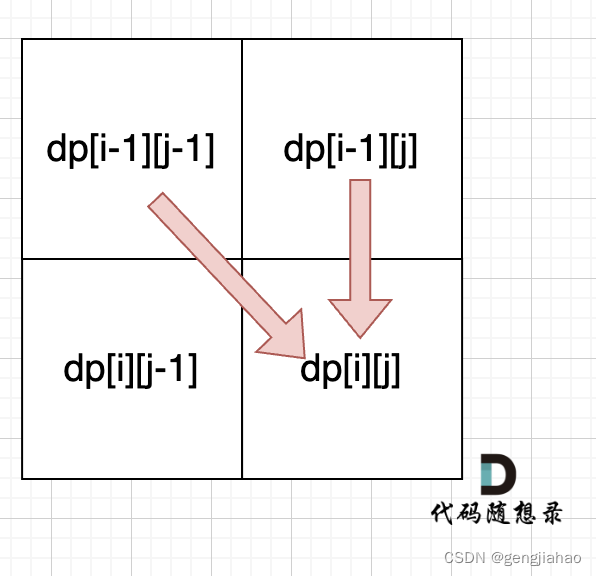
所以遍歷的時候一定是從上到下，從左到右，這樣保證dp[i][j]可以根據之前計算出來的數值進行計算。

for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}
}

5. 舉例推導dp數組

以s：“baegg”，t："bag"為例，推導dp數組狀態如下：

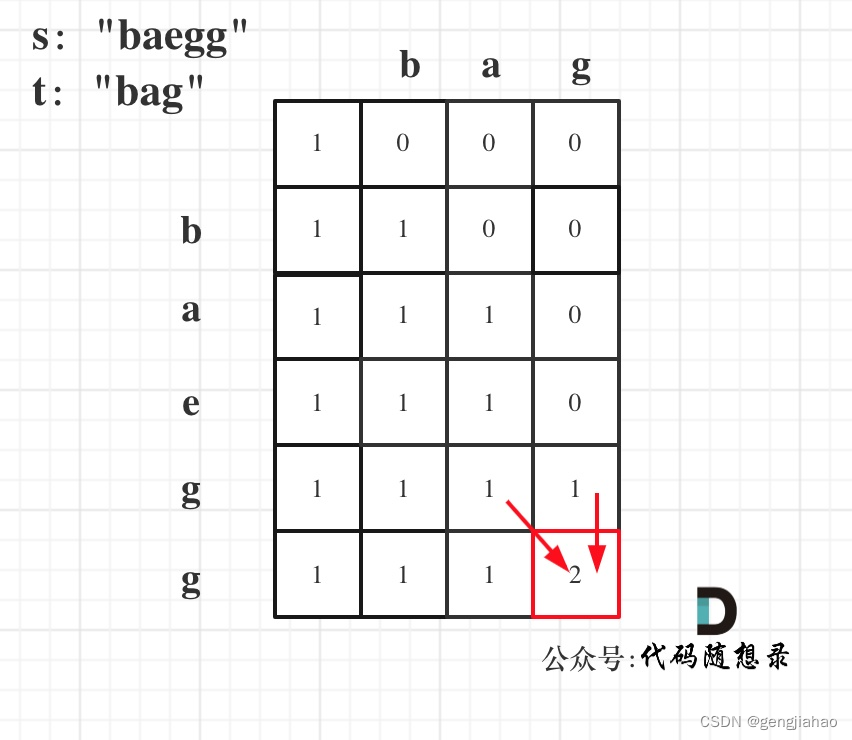
代碼：

python

class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(len(s)):dp[i][0] = 1for j in range(1, len(t)):dp[0][j] = 0for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]else:dp[i][j] = dp[i-1][j]return dp[-1][-1]