數據結構–最短路徑 Dijkstra算法

Dijkstra算法

$計算begin點到各個點的最短路$

如果是無向圖，可以先把無向圖轉化成有向圖

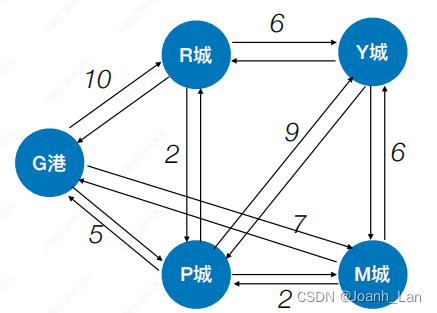
我們需要2個數組
final[] （標記各頂點是否已找到最短路徑）與 dis[] （最短路徑?度）數組

Dijkstra算法是一種用于尋找圖中最短路徑的算法，它的步驟如下：

1. 初始化：將起始節點的最短路徑設置為0，其他節點的最短路徑設置為正無窮大。
2. 選取最短路徑最小的節點作為當前節點。
3. 更新當前節點的鄰居節點的最短路徑：如果通過當前節點到達鄰居節點的路徑比鄰居節點當前的最短路徑更短，則更新鄰居節點的最短路徑。
4. 標記當前節點為已訪問(已經找到 $begin$ 到該點的最短路)。
5. 重復步驟2 $\to$ 4，直到所有節點都被訪問過或者沒有可達到的節點。
6. 根據最短路徑和前驅節點構建最短路徑樹或者路徑數組。

以上就是Dijkstra算法的基本步驟。在實際應用中，可以使用優先隊列來選取最短路徑最小的節點，以提高算法的效率 (堆Dijkstra)。

V0到V2 的最短(帶權)路徑?度為：dist[2] = 9
通過 path[ ] 可知，V0到V2 的最短(帶權)路徑：
$v_0\to v_4\to v_1\to v_2$

Dijkstra算法的時間復雜度

時間復雜度： $O(n^2)即O(|V{|}^2)$

代碼實現

int g[N][N]; // 存儲每條邊
int dist[N]; // 存儲1號點到每個點的最短距離
bool st[N]; // 存儲每個點的最短路是否已經確定
//時間復雜是 O(n2+m), n 表示點數，m 表示邊數
// 求1號點到n號點的最短路，如果不存在則返回-1
int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i++){int t = -1; // 在還未確定最短路的點中，尋找距離最?的點for (int j = 1; j <= n; j++)if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;// ?t更新其他點的距離for (int j = 1; j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}if (dist[n] == 0x3f3f3f3f)return -1;return dist[n];
}

負權值帶權圖問題,Dijkstra不可用

$負權值帶權圖問題，Dijkstra不可用！！！$

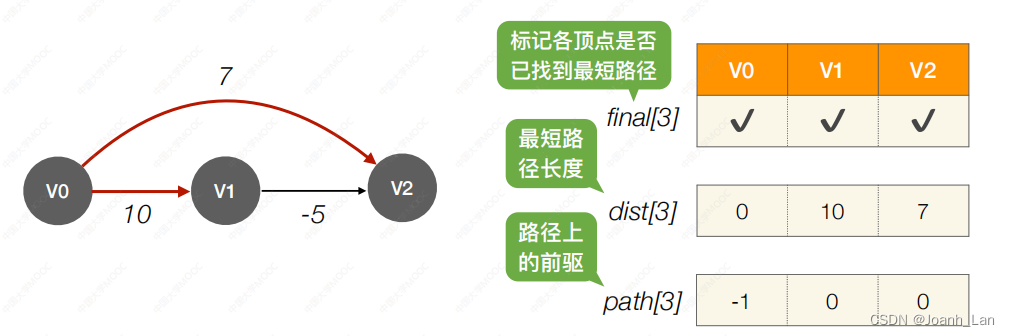
事實上$V_0$ 到 $V_2$ 的最短帶權路徑?度為 5
結論：Dijkstra 算法不適?于有負權值的帶權圖