As there is a lot of buzz about AutoML, I decided to write about the original AutoML; step-wise regression and best subset selection. Then I decided to ignore step-wise regression because it is bad and should probably stop being taught. That leaves best subset selection to discuss.

由于有關AutoML的話題很多，因此我決定寫有關原始AutoML的文章。 逐步回歸和最佳子集選擇。 然后我決定忽略逐步回歸，因為它很糟糕 ，應該停止講授。 剩下的最佳子集選擇需要討論。

The idea behind best subset selection is choose the “best” subset of variables to include in a model, looking at groups of variables together as opposed to step-wise regression which compares them one at a time. We determine which set of variables are “best” by assessing which sub-model fits the data best while penalizing for the number of independent variables in the model to avoid over-fitting. There are multiple metrics for assessing how well a model fits: adjusted 𝑅-squared, the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC), and Mallow’s 𝐶𝑝 are probably the best known.

最佳子集選擇的思想是選擇要包括在模型中的變量的“最佳”子集，將變量組放在一起查看，而不是逐步比較一次將它們進行比較的逐步回歸。 我們通過評估哪個子模型最適合數據，同時對模型中自變量的數量進行懲罰以避免過度擬合，從而確定哪個變量組“最佳”。 有多種評估模型擬合程度的指標：調整后的𝑅平方，Akaike信息準則(AIC)，貝葉斯信息準則(BIC)和Mallow's𝐶𝑝 是最有名的。

The formulas for each are below.

每個公式如下。

With Adjusted R-squared, you want to find the model with the largest Adjusted R-squared because it explains the most variance in the dependent variable, penalized for model complexity. For the others, you want to find the model with the smallest Information Criterion because it is the model with the least unexplained variance in the dependent variable, penalizing for model complexity. They’re the same idea, i.e. maximizing something good versus minimizing something bad.

使用“已調整R平方”時，您要查找“已調整R平方”最大的模型，因為它解釋了因變量中最大的方差，并因模型復雜性而受到懲罰。 對于其他模型，您希望找到信息準則最小的模型，因為它是因變量中無法解釋的方差最小的模型，因此對模型的復雜性不利。 他們是同一主意，即最大化好事物與最小化壞事物。

Both the AIC and Mallow’s 𝐶𝑝 tend to give better predictive models, while BIC tends to give models with fewer independent variables because it penalizes complex models more than the other two.

AIC和Mallow的𝐶𝑝 BIC傾向于提供更好的預測模型，而BIC傾向于提供具有更少自變量的模型，因為它比其他兩個模型對復雜模型的懲罰更大。

Like most things in life, automating model selection comes at a cost. If you use your data to select a linear model, the coefficients of the selected variables will be biased away from zero! The null hypotheses of both the individual t-tests for each coefficient and the F-test for overall model significance are based on the assumption that each coefficient is normally distributed with mean 0. Since we have introduced bias into our coefficients, the Type I error level increases for these tests! This may not be an issue if you just need a predictive model, but it completely invalidates any statistical inferences made with the selected model. AutoML may be able to generate decent predictive models, but inference still requires a person to think carefully about the problem and follow the scientific method.

就像生活中的大多數事情一樣，自動選擇模型是有代價的。 如果您使用的數據來選擇線性模型，所選擇的變量的系數將從0 偏向了！ 每個系數的單獨t檢驗和整體模型顯著性的F檢驗的零假設均基于以下假設：每個系數的正態分布均值為0。由于我們在系數中引入了偏差，因此I型錯誤這些測試的水平提高了！ 如果您只需要預測模型，這可能就不成問題了，但是這完全會使使用所選模型做出的任何統計推斷無效。 AutoML可能能夠生成不錯的預測模型，但是推理仍然需要人們仔細考慮問題并遵循科學方法。

展示最佳子集選擇的偏見 (Demonstrating the Bias of Best Subset Selection)

I performed a simulation study to demonstrate the bias caused by best subset selection. Instead of looking at the bias in the coefficients, we will look at the bias in the estimated standard deviation of the error term in the model

我進行了仿真研究，以證明最佳子集選擇所引起的偏差。 除了查看系數中的偏差之外，我們還將查看模型中誤差項的估計標準偏差中的偏差。

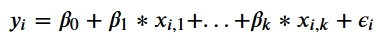
where the error terms are identically and independently distributed 𝑁(0,𝜎) random variables.

其中誤差項是相同且獨立分布的𝑁(0，𝜎)隨機變量。

At each round of the simulation, a sample of 100 observations are generated from the same distribution. The true model, which contains only the truly significant variables, as well as the best subset models selected by AIC and BIC are also estimated. From each model, I estimate the 𝜎 of the error term using the formula

在模擬的每一輪中，從同一分布生成100個觀測值的樣本。 還估計僅包含真正重要變量的真實模型，以及由AIC和BIC選擇的最佳子集模型。 從每一個模型，我估計σ 使用公式計算誤差項

This is performed 500 times.

這執行了500次。

The particular parameters of my simulation are as follows: 𝑛 = 100, # of independent variables = 6, 𝜎 = 1, and the number of significant independent variables is 2. The intercept is significant as well, so 3 coefficients are non-zero. The non-zero coefficients are selected using 𝑁(5,1) random numbers because I am too lazy to define fixed numbers, but they remain fixed for all rounds of the simulation.

我的模擬的特定參數如下： 𝑛 = 100，自變量= 6，σ= 1，和顯著獨立變量的數目的＃是2。截距是顯著為好，這樣的3個系數為非零。 非零系數是使用𝑁(5,1)隨機數選擇的，因為我懶于定義固定數，但是在所有模擬回合中它們都保持固定。

I first defined my own function to perform best subset selection using AIC or BIC using a naive approach by looking at every combination of variables. It only works for a small number of variables because the number of models it has to consider blows up as the number of variables increases. The number of models considered is

我首先定義了自己的函數，以天真的方法通過查看變量的每種組合來使用AIC或BIC來執行最佳子集選擇。 它僅適用于少量變量，因為隨著變量數量的增加，必須考慮的模型數量會激增。 考慮的模型數量是

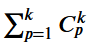
but smarter implementations of best subset selection use a tree search to reduce the number of models considered.

但是最佳子集選擇的更智能實現使用樹搜索來減少所考慮模型的數量。

The graphs of interest are below these chunks of code for the best subset selection function and for the simulation.

感興趣的圖在這些代碼塊的下方，用于最佳子集選擇功能和仿真。

The red line is the line where the y-axis equals the x-axis, which is the unbiased estimate of 𝜎 from the true model. As you can see in the plots below, the estimates of 𝜎 are biased from the models selected by best AIC and BIC. In fact they will always be less than or equal to the unbiased estimate of 𝜎 from the true model. This demonstrates why models selected via best subset selection are invalid for inference.

紅線是y軸等于x軸的線，這是真實模型中𝜎的無偏估計。 如下圖所示， 𝜎的估計值是從最佳AIC和BIC選擇的模型中得出的。 實際上，它們將始終小于或等于真實模型中𝜎的無偏估計。 這說明了為什么通過最佳子集選擇所選擇的模型對于推理無效。

獎勵部分：調查LASSO和嶺回歸中誤差項的估計標準偏差的偏差 (Bonus Section: Investigating Bias in Estimated Standard Deviation of the Error term in LASSO and Ridge Regression)

While working on the simulation study above, I became interested in the potential bias of regularization methods on estimates of the standard deviation of the error term in a linear model, although one wouldn’t use a regularized model to estimate a parameter for the purposes of inference. As you most likely know, LASSO and Ridge regression intentionally bias estimated coefficients towards zero to reduce the amount of variance in the model (how much estimated coefficients change from sample to sample from the same population). The LASSO can set coefficients equal to zero, performing variable selection. Ridge regression biases coefficients towards zero, but will not set them equal to zero, so it isn’t a variable selection tool like best subset selection or the LASSO.

在進行上述仿真研究時，我對正則化方法對線性模型中誤差項的標準偏差的估計的潛在偏差感興趣，盡管出于以下目的，人們不會使用正則化模型來估計參數：推理。 如您最可能知道的那樣，LASSO和Ri??dge回歸有意將估計系數偏向零，以減少模型中的方差量(在同一總體中，樣本之間的估計系數變化了多少)。 LASSO可以將系數設置為零，從而執行變量選擇。 嶺回歸將系數偏向零，但不會將其設置為零，因此它不是像最佳子集選擇或LASSO這樣的變量選擇工具。

I used the same set up as before, but upped the sample size from 100 to 200, the number of independent variables from 6 to 100, and the number of significant independent variables from 2 to 50. The shrinkage parameter in both the LASSO and Ridge models were chosen among 0.01, 0.1, 1.0, and 10.0 using 3-fold cross validation. I counted the number of non-zero coefficients in the LASSO model for purposes of calculating 𝜎? and used all 100, plus 1 for the intercept, for the Ridge model, since it biases coefficients to zero but doesn’t set them to zero.

我使用了與以前相同的設置，但是樣本量從100增加到200，自變量從6增加到100，有效自變量從2增加到50。LASSO和Ri??dge中的收縮參數使用3倍交叉驗證從0.01、0.1、1.0和10.0中選擇模型。 我數的非零系數的數目在LASSO模型用于計算σ的目的，所使用的所有100，再加上1截距，對于嶺模型，因為它偏置系數為零，但不將它們設置為零。

Obviously, regularized linear models are not valid for the purposes of inference because they bias estimates of coefficients. I still thought investigating any bias in the estimated standard deviation of the error term was worth writing a little code.

顯然，正則化線性模型出于推論的目的是無效的，因為它們會使系數的估計產生偏差。 我仍然認為調查誤差項的估計標準偏差中的任何偏差都值得編寫一些代碼。

The plots are below this code chunk for the simulations.

用于仿真的圖在此代碼塊下方。

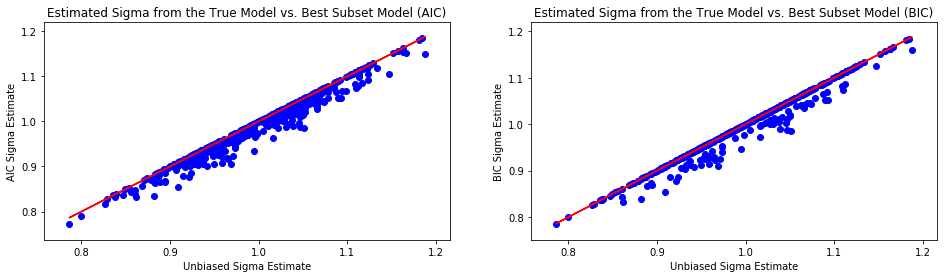
By visual inspection, 𝜎? appears biased downwards in the LASSO models, but the unbiased estimate doesn’t form an upper bound as it does with the best AIC and BIC models. The Ridge models do not show obvious bias in estimating this parameter. Let’s investigate with a paired t-test, since the estimates are derived from the same sample at each iteration. I’m using the standard p-value cutoff of 0.05, because I’m too lazy to decide my desired power of the test.

通過目視檢查，在LASSO模型中𝜎?出現向下偏差，但與最佳AIC和BIC模型一樣，無偏差估計值不會形成上限。 Ridge模型在估計此參數時沒有顯示明顯的偏差。 讓我們用配對t檢驗進行研究，因為估計是在每次迭代時從相同的樣本得出的。 我使用的標準p值截止值為0.05，因為我太懶了，無法確定所需的測試功效。

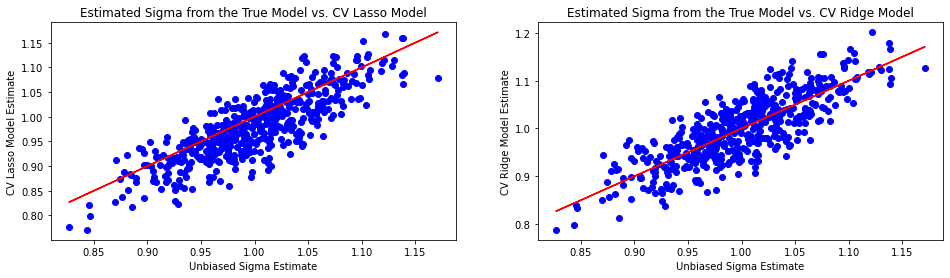
As guessed by the visual inspection, there is insufficient evidence for a difference in means between the estimates of 𝜎? , from the true and Ridge models. However, there is sufficient evidence at the 0.05 significance level to conclude that the LASSO models tended to make downwardly biased estimates of 𝜎?. Whether or not this is a generalizable fact is unknown. It would require a formal proof to make a conclusion.

由于猜測由目視檢查，對在σ的估計方法之間的差異，從真與嶺車型證據不足。 然而，在0.05的顯著性水平足夠的證據得出的結論是套索模型傾向于使σ向下偏估計。 這是否是一個普遍的事實還不得而知。 得出結論需要正式證明。

Thanks for making it to the end. Although using the data to select a model invalidates classical inference assumptions, post-selection inference is a hot area of statistical research. Perhaps we’ll be talking about AutoInference in a few years.

感謝您的努力。 盡管使用數據選擇模型會使經典推論假設無效，但是選擇后推論是統計研究的熱門領域。 也許幾年后我們會談論自動推理。

All of my code for this project can be found here.

我在這個項目中的所有代碼都可以在這里找到。