論文閱讀——Adversarial Eigen Attack on Black-Box Models

Adversarial Eigen Attack on Black-Box Models

作者：Linjun Zhou， Linjun Zhou

攻擊類別：黑盒（基于梯度信息），白盒模型的預訓練模型可獲得，但訓練數據和微調預訓練模型的數據不可得（這意味著模型的網絡結構和參數信息可以獲得）、目標攻擊+非目標攻擊
白盒+黑盒組合使用，白盒利用了中間表示，黑盒利用了輸出得分。

疑問
Q1: 基于梯度信息生成對抗樣本，如何保證遷移能力
A1: 似乎沒有像常規方法一樣考慮遷移性
Q2: 預訓練模型選的啥？
A2: 用不到預訓練模型

解決的問題：

替代模型的訓練需要已知訓練數據+降低查詢量+保證擾動小

替代模型的訓練需要已知訓練數據：白盒模型的特征表示和黑盒模型的輸出概率得分；
降低查詢量：根據方向當屬估計梯度減少梯度估計采樣的樣本，使用截斷奇異值確定進一步降低查詢量；
保證擾動小：每次擾動的尋優都約束到 $L_2$ 范數球上。

黑盒攻擊現狀

黑盒攻擊分為兩類：
基于梯度估計的對抗攻擊: 描述了一個純黑盒攻擊設置，其中可用的信息只是黑盒模型的輸入和輸出。在此設置中使用的常用技術是零階優化[8]。與白盒攻擊不同的是，黑盒攻擊中不存在與網絡參數相關的梯度信息。梯度需要通過采樣不同方向的擾動和匯總與輸出相關的某個損失函數的相對變化來估計。
基于替代模型（substitute model）的對抗攻擊:使用來自訓練數據集的側信息。通常，在給定的訓練數據集上訓練一個替代的白盒模型。

方案概述：

將白盒攻擊和黑盒攻擊相結合。通過將白盒模型的中間表示到黑盒模型輸出的映射看作一個黑盒函數，在表示空間上形成一個替代的黑盒攻擊設置，可以應用黑盒攻擊的常見做法。另一方面，從原始輸入到中間表示層的映射是預訓練模型的一部分，可以看作是一個白盒設置。值得注意的是，該框架可以處理兩個模型相同或不同的分類類別，增強了其實際應用場景。使用預訓練白盒網絡的表示空間有助于提高黑盒模型的攻擊效率的主要原因是，深度神經網絡的較低層，即表示學習層，在不同的數據集或數據分布之間是可轉移的。

白盒模型：

$\circ h(x)$ ， $h (x)$ 表示原始輸入到低維表示空間的映射， $g$ 表示輸出概率的表示空間映射， $g:{\mathbb{R}^m} \to {[0,1]^{{c_w}}}$ ， ${c_w}$ 表示G輸出類別的數量；

黑盒模型：

$F:{\mathbb{R}^n} \to {[0,1]^{{c_b}}}$ , ${c_b}$ 表示F輸出類別的數量， ${c_b}$ 和 ${c_w}$ 可能不相等。

疑問
Q1: 如何對齊白盒模型和黑盒模型的輸出概率分布的？存在兩種情況：黑盒模型和白盒模型的輸出概率分布不一致或者輸出概率類別的長度可能不同？
A1: 為解決上述問題，作者并沒有使用白盒模型的參數，而是使用白盒模型的中間表示 $z = h (x)$ 和新的映射函數 $\tilde g:{\mathbb{R}^m} \to {[0,1]^{{c_b}}}$ （被攻擊黑盒模型的輸出的表示空間）。類比白盒模型的定義，若 $\tilde g$ 存在，則可獲得黑盒模型 $\tilde g \circ h(x)$ 。

基于上述定義，黑盒攻擊的優化目標函數為：

$\mathop {\min }\limits_\delta {p_F}(y|x + \delta ) \Rightarrow \mathop {\min }\limits_\delta {p_{g \circ h}}(y|x + \delta ){\text{ }}s.t.,{\text{ }}||\delta |{|_2} < \rho$
${x_{t + 1}} = {x_t} - \varepsilon {\nabla _x}[F(x;\theta )]$ (1)

${\nabla _x}[F(x;\theta )]$ 通過采樣一些擾動和匯總輸出的相對變化來估計,但是在每次迭代時估計梯度，會消耗的大量的樣本，這不利于提升攻擊效率。為解決這一問題作者將梯度 ${\nabla _x}[F(x;\theta )]$ 拆分如下：

${\nabla _x}[F(x;\theta )] = {J_h}{(x)^T}{\nabla _z}[\tilde g{(z;\tilde \theta )_y}]$ (2)

${J_h}{(x)}$ 是關于 $h$ 的 $m ? n$ 雅克比矩陣 $\frac{{\partial ({z_1},{z_2}, \cdots ,{z_m})}}{{\partial ({x_1},{x_2}, \cdots ,{x_n})}}$ , $z$ 是特征空間表示，也就是 $h$ 的輸出。但 ${\nabla _z}[\tilde g{(z;\tilde \theta )_y}]$ 中 $\tilde g$ 是黑盒模型，因此需要采樣估計 ${\nabla _z}[\tilde g{(z;\tilde \theta )_y}]$ 。 $y$ 表示 $\tilde g$ 輸出的第 $y$ 個成分。

根據方向倒數的定義可知，
${\nabla _z}[\tilde g{(z;\tilde \theta )_y}] = \sum\limits_{i = 1}^m {(\frac{{\partial \tilde g{{(z;\tilde \theta )}_y}}} {{\partial {{\vec l}_i}}}{|_z} \cdot \vec l)} ,{{\vec l}_1},{{\vec l}_2}, \cdots ,{{\vec l}_m}{\text{ are orthogonal}}$ (3)

我們可以通過每次迭代使用m個樣本，從一組正交基中迭代地設置 $z$ 的擾動方向，來估計 ${\nabla _z}[\tilde g{(z;\tilde \theta )_y}]$ 。但是使用上述方法估計 ${\nabla _z}[\tilde g{(z;\tilde \theta )_y}]$ 會消耗巨大的查詢預算。為解決這一問題，作者通過犧牲估計精度來降低查詢量。具體而言，首先設計EigenBA算法來尋找表示空間的標準基，

${{\vec l}_i} = {J_h}(x){\delta _i}$ (4)

${\delta _i}$ 是原始輸入空間上的擾動，會導致表示空間變成 ${{\vec l}_i}$ 。最優的擾動可求解為：
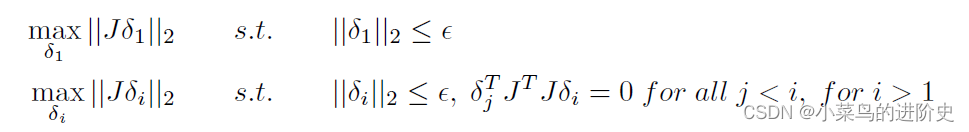
在這里插入圖片描述
作者對上述等式求解獲得最優的 ${\delta _1},{\delta _2}, \cdots ,{\delta _m}$

因此，如果我們將擾動依次迭代采樣到 ${\delta _1},{\delta _2}, \cdots ,{\delta _m}$ ，則一步實際擾動 ${\nabla _x}[F(x;\theta )]$ 可以用公式2和式3來近似，并且，由于特征值的跡可能很小，即表征空間的擾動范數可能對具有相應特征向量方向的原始輸入空間上的擾動不敏感。為了在不犧牲太多攻擊效率的情況下減少查詢數，作者只保留探測的top-K擾動， ${\delta _1},{\delta _2}, \cdots ,{\delta _K}$ 。通過對雅可比矩陣J進行截斷奇異值分解(SVD)，只保留前K個分量，可以快速計算出 ${J^T}J$ 的特征向量。

上述過程的偽代碼如下：
在這里插入圖片描述
迭代擾動尋優過程中的參數定義似乎不全！

實驗

1、數據集：ImageNet、Cifar-10
2、對比方法：SimBA-DCT、Trans-FGM
3、評估指標：攻擊一張樣本的平均查詢量、攻擊成功率、對抗擾動的 ${L_2}$ 和 ${L_\infty }$ 范數
4、實驗模塊：不同查詢量下非目標攻擊和目標攻擊的攻擊性能測試+消融研究

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/38800.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/38800.shtml
英文地址，請注明出處：http://en.pswp.cn/news/38800.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！