數據結構與算法：樹狀數組

前言

太難了……

一、樹狀數組使用場景

樹狀數組一般用來維護可差分的信息，比如累加和，累乘積等。舉個例子，當整個數組的累加和為sum1，一個區間內的累加和為sum2，那么除了這個區間剩下部分的累加和就是sum1-sum2，這就是可差分的信息。

不可差分的信息，如最大值和最小值，一般用線段樹來維護。線段樹雖然幾乎可以完全替代樹狀數組，但代碼量較多，常數時間比較大。

二、樹狀數組常見用法

1.一維數組上單點增加、范圍查詢

（1）原理詳解

雖然單點增加直接在原數組上操作即可，但對于范圍查詢，以現有的知識，肯定就是構建前綴和數組，然后每次輸出范圍累加和即可。但每次單點增加時，都需要從這個點開始遍歷前綴和數組到結尾，把每個位置都加上這個增加的數，那這樣的時間復雜度就很高了。

樹狀數組可以實現每次單點增加和范圍查詢的時間復雜度均為O(logn)，這個復雜度相比每次都遍歷的O(n)要優秀太多了。

首先要銘記！樹狀數組的下標必須以1開始！樹狀數組的所有操作都是基于這一點的！

接著，先將數組按上圖方式從左到右劃分原數組。方法就是，首先規定每個區間的長度為2的冪，那么最小的區間長度就是2的0次方，即1長度，之后長度每次乘以2。那么以1長度的區間劃分數組的話，每個區間里就只有自己那個位置的數，可以將數組劃分成數組長度個區間。之后以2長度劃分，所以每個區間里就有兩個數，比如第一個區間里是1位置和2位置兩個數，第二個區間里是3位置和4位置的數。之后一直到16長度，即整個數組都在這個區間內。注意，區間要一直增長到能把整個數組包住，數組長度不夠了不要緊。

之后，樹狀數組index-tree[i]的定義是，原數組中以i為右邊界，最長的一個區間的累加和。那么1位置的值就是原數組中以1位置為右邊界的最長區間，那就是1位置自己，所以值為1。之后2位置的值就是原數組中以2位置有右邊界的最長區間，那么就是長度為2的區間，包括1位置和2位置，所以值就是2。之后4位置的值包括1到4位置，所以就是4。還有12位置就是原數組中以12為右邊界的最長區間，那么就是長度為4，包括9~12位置的區間，所以值也是4。之后以此類推8位置就是8,16位置就是16。

所以，樹狀數組中，i位置負責的區間包括的范圍的左邊界，就是i這個數去掉自己二進制的最右的1后再加1。舉個例子，12的二進制為1100，去掉最右的1就是1000，再加1就是1001，對應的十進制數就是9，所以tree[12]負責的區間就是9~12，和上面的定義一致。

（別看上圖寫的，估計當時腦子抽了筆誤了）

之后，如果要求原數組1~i范圍上的累加和，那么先加上樹狀數組中i位置的值，再移除這個i的最右側的1，然后加上移除后的i位置的值，直到i等于0。

舉個例子，假如要求原數組1~15范圍上的前綴和，那么就是先加上tree[15]，即原數組15~15范圍上的數的累加和。再移除15最右側的1，變成14，然后加上tree[14]，即原數組13~14范圍上的數的累加和。再移除14最右側的1變成12，然后加上tree[12]，即原數組9~12范圍上的數的累加和。再移除12最右側的1變成8，然后加上tree[8]，即原數組1~8范圍上的數的累加和。此時再移除最右側的1就變成0了，所以停止。可以發現，這樣加下來正好是1~15范圍上的數的累加和。

對于單點增加的操作，就需要在樹狀數組中所有包括該點的區間的位置上全進行增加。方法是，如果要在原數組的i位置增加v，那么先在樹狀數組中的i位置增加v，因為必然包括i這個位置。之后每次讓i加上自己最右側的1，然后在新的i位置增加v，直到i越界。

舉個例子，假如要在原數組的11位置增加3，那么就是先在tree[11]上加3。然后由于11的二進制為01011，所以加上最右側的1變成01100，即12，那么就在tree[12]上加3。然后再加上最右側的1變成10000，即16，那么就在tree[16]上加3，之后越界停止。可以發現，原數組的11位置，被且只被tree[11]，tree[12]，tree[16]代表的區間包括。

所以對于范圍查詢的操作，只需要用1~r范圍上的累加和減去1~l-1范圍上的累加和即可。

（2）模板——樹狀數組 1

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=5e5+5;
int n,m;//樹狀數組
vector<int>tree(MAXN);//提取最右側1
int lowbit(int i)
{return i&-i;
}//加
void add(int i,int v)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}//1~i累加和
int sum(int i)
{int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//范圍查詢
int query(int l,int r)
{return sum(r)-sum(l-1);
}void solve()
{cin>>n>>m;//利用add方法建樹狀數組for(int i=1,v;i<=n;i++){cin>>v;add(i,v);}for(int i=0,type;i<m;i++){cin>>type;if(type==1){int x,k;cin>>x>>k;add(x,k);}else{int l,r;cin>>l>>r;cout<<query(l,r)<<endl;}}}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

樹狀數組雖然原理挺難的，但代碼其實很簡單。

首先是lowbit函數負責求i這個數最右側的1，直接i&(-i)即可。

之后是add函數，只要i小于等于n，即沒越界，那就每次讓tree[i]加上v，然后i增加lowbit(i)即可。

sum函數負責返回原數組1~i范圍上的數的累加和，那就是只要i大于0，每次讓ans加上tree[i]，然后i減去lowbit(i)，最后返回ans即可。

所以query范圍查詢只需要返回sum(r)-sum(l-1)即可。

既然有了add方法，一開始構建樹狀數組的時候直接調用就行了。

2.一維數組上范圍增加、單點查詢

（1）原理詳解

范圍增加就需要一點思考了。

首先，原數組arr的差分數組D[i]的定義是arr[i]-arr[i-1]，所以arr[i]就是差分數組D從1~i的前綴和。之后，不對原數組構建樹狀數組，而是對原數組的差分數組D構建樹狀數組。所以單點查詢就是求差分數組1~i的前綴和，那直接調用sum方法就行了。對于范圍增加，那就和一維差分一樣，在差分數組的l位置加上v，在r+1位置減去v，那直接調用兩次原本的add方法即可。

（2）模板——樹狀數組 2

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=500000+5;//樹狀數組 -> 維護差分數組
vector<int>tree(MAXN);
int n,m;int lowbit(int i)
{return i&-i;
}//原始add
void add(int i,int v)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}int sum(int i)
{int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//新add
void add(int l,int r,int v)
{add(l,v);add(r+1,-v);
}//新query
int query(int i)
{return sum(i);
}void solve()
{cin>>n>>m;for(int i=1,v;i<=n;i++){cin>>v;add(i,i,v);}for(int i=0,type;i<m;i++){cin>>type;if(type==1){int l,r,v;cin>>l>>r>>v;add(l,r,v);}else{int x;cin>>x;cout<<query(x)<<endl;}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

代碼沒啥好說的，和上面描述的一樣。

3.一維數組上范圍增加、范圍查詢

這個就已經到了線段樹的領域了。

（1）原理詳解

首先先考慮原數組1~k范圍上的累加和的求法，如果有了這個方法那么范圍查詢的事就解決了。還是考慮引入差分數組，那么就可以將原數組的累加和轉化成差分數組的累加和。之后合并可得，一共需要加k個D[1]，k-1個D[2]，一直到k-(k-1)，即1個D[k]，那么再提取出k并寫成數學表達式就是如上圖所示。因為有兩個未知量，所以考慮構建兩個樹狀數組分別維護原始差分數組和(i-1)D[i]這個新數組。

（2）模板——線段樹 1

byd抽象起來了。

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=1e5+5;//維護差分數組
vector<ll>tree1(MAXN);
//維護(i-1)*Di數組
vector<ll>tree2(MAXN);int n,m;int lowbit(int i)
{return i&-i;
}//原始add，告訴在哪棵樹上add
void add(vector<ll>&tree,int i,ll v)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}//原始1~i的累加和
ll sum(vector<ll>&tree,int i)
{ll ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//原數組中[l……r]+v
void add(int l,int r,ll v)
{add(tree1,l,v);add(tree1,r+1,-v);add(tree2,l,(l-1)*v);add(tree2,r+1,-r*v);
}//1~k的累加和
ll query(int k)
{return k*sum(tree1,k)-sum(tree2,k);
}//原數組范圍累加和
ll query(int l,int r)
{return query(r)-query(l-1);
}void solve()
{cin>>n>>m;for(int i=1;i<=n;i++){ll v;cin>>v;add(i,i,v);}for(int i=0,type;i<m;i++){cin>>type;if(type==1){ll l,r,v;cin>>l>>r>>v;add(l,r,v);}else{int l,r;cin>>l>>r;cout<<query(l,r)<<endl;}}    
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

代碼就是完全根據上面思路寫的，就是幾個函數套函數實現的。

原數組范圍累加和就是調用兩次原數組1~k范圍累加和，原數組1~k范圍累加和再使用公式計算，那還需要調用兩個樹狀數組維護的差分數組1~k上的累加和。然后每次范圍增加都要分別調用兩次兩個樹狀數組的單點增加。

4.二維數組上單點增加、范圍查詢

二維的題不管是用樹狀數組還是線段樹都很難，所以基本很少見。

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;//二維樹狀數組
vector<vector<int>>tree;int n,m;int lowbit(int i)
{return i&-i;
}//單點增加 -> O(logn*logm)
void add(int x,int y,int v)
{for(int i=x;i<=n;i+=lowbit(i)){for(int j=y;j<=m;j+=lowbit(j)){tree[i][j]+=v;}}
}//(1,1)->(x,y)的累加和
int sum(int x,int y)
{int ans=0;for(int i=x;i>0;i-=lowbit(i)){for(int j=y;j>0;j-=lowbit(j)){ans+=tree[i][j];}}return ans;
}//范圍查詢
int query(int a,int b,int c,int d)
{//二維差分return sum(c,d)-sum(a-1,d)-sum(c,b-1)+sum(a-1,b-1);
}void solve()
{cout<<"VIP題,沒法做,所以就只有代碼了……"<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

二維數組的單點增加和范圍查詢基本和二維差分一樣，就是構建二維樹狀數組維護二維差分數組。然后單點增加和一維的單點增加類似，是兩個循環嵌套。然后(1,1)到(x,y)范圍上的累加和也和一維的類似，范圍查詢就是二維前綴和數組求范圍累加和的公式。

5.二維數組上范圍增加、范圍查詢

太抽象了……

（1）原理詳解

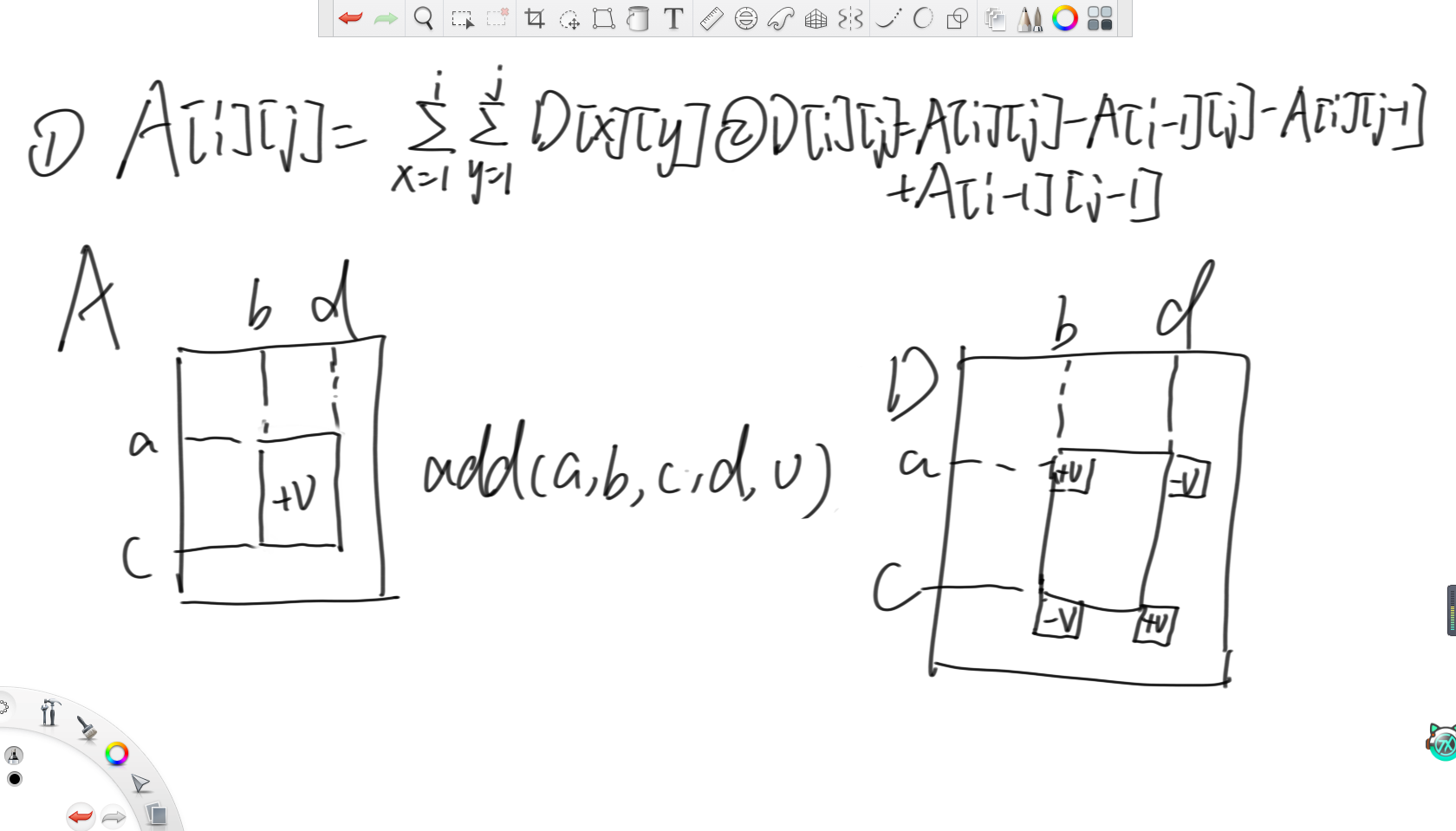
二維數組上的范圍增加還是利用二維差分數組，根據二維差分可得，原數組上A[i][j]的值就是差分數組從(1,1)一直求和到(i,j)，差分數組D[i][j]的值就是原數組這個位置的值減去上方格子，左側格子和左上格子。

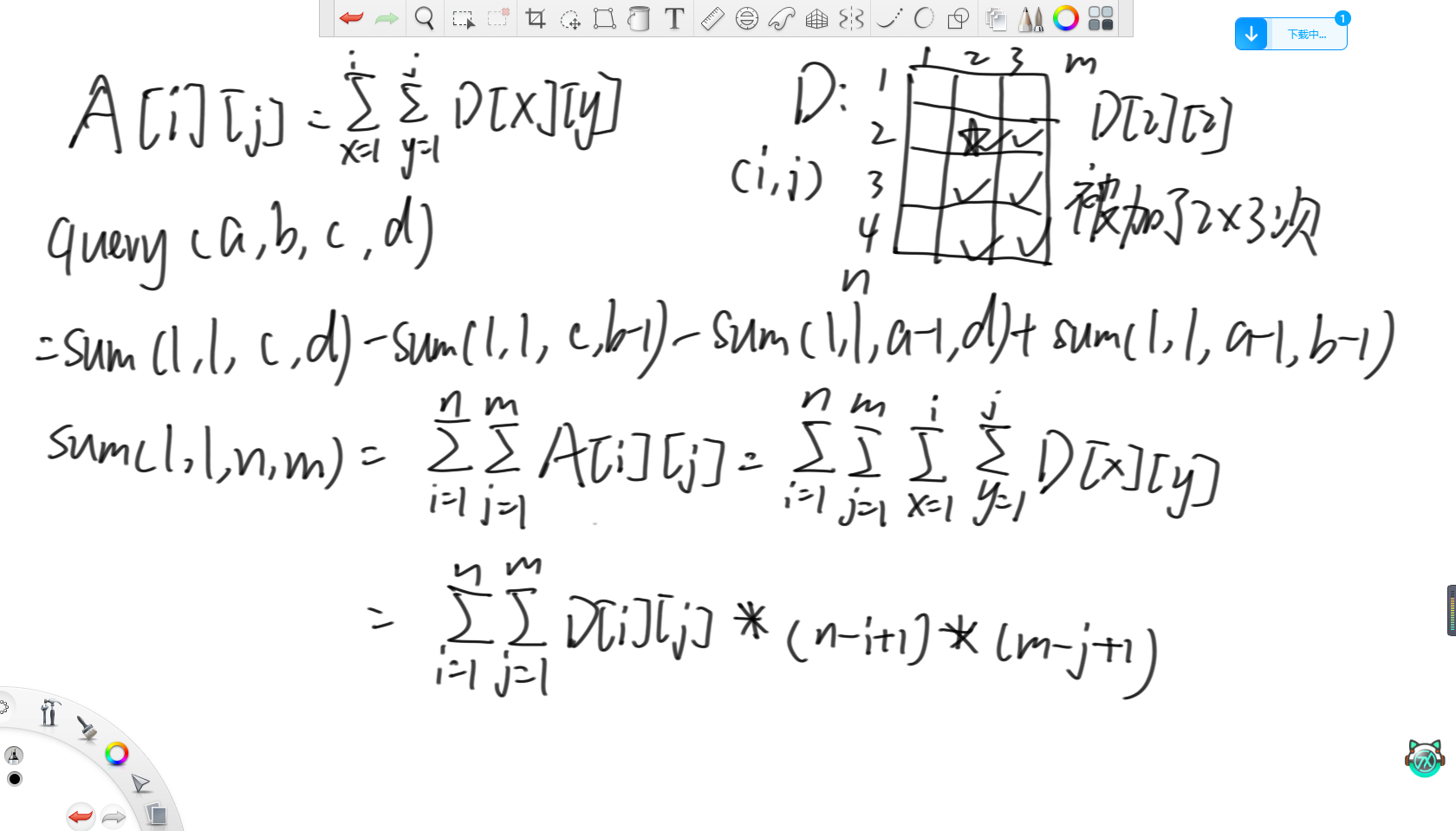
根據二維前綴和，原數組的范圍查詢就要調用四次二維前綴和，所以解決求(1,1)到(n,m)累加和的問題就可以了。那么就需要考慮如何在差分數組中求累加和，所以可以得到這個四層循環嵌套的形式，之后肯定需要對其進行化簡。觀察上述例子，在求(1,1)到(4,3)的過程中，D[2][2]一共被加了2*3=6次，即當(i,j)來到(2,2)到(4,3)這個范圍內時才會把這個格子加一遍。所以這個四層循環的公式可以化簡為只和(i,j)有關的最終形式。

再將這個最終形式化簡，就可以得到如上的形式，所以就需要用四個樹狀數組分別維護這四個信息。每次增加都對這四個差分數組進行操作。

（2）模板——上帝造題的七分鐘

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=2048+5;
const int MAXM=2048+5;int n,m;//D[i][j]的樹狀數組
vector<vector<int>>tree1(MAXN,vector<int>(MAXM));
//D[i][j]*i的樹狀數組
vector<vector<int>>tree2(MAXN,vector<int>(MAXM));
//D[i][j]*j的樹狀數組
vector<vector<int>>tree3(MAXN,vector<int>(MAXM));
//D[i][j]*i*j的樹狀數組
vector<vector<int>>tree4(MAXN,vector<int>(MAXM));int lowbit(int i)
{return i&-i;
}//單點增加
void add(int x,int y,int v)
{int v1=v;int v2=x*v;int v3=y*v;int v4=x*y*v;for(int i=x;i<=n;i+=lowbit(i)){for(int j=y;j<=m;j+=lowbit(j)){tree1[i][j]+=v1;tree2[i][j]+=v2;tree3[i][j]+=v3;tree4[i][j]+=v4;}}
}//(1,1)->(x,y)求和
int sum(int x,int y)
{int ans=0;for(int i=x;i>0;i-=lowbit(i)){for(int j=y;j>0;j-=lowbit(j)){ans+=(x+1)*(y+1)*tree1[i][j]-(y+1)*tree2[i][j]-(x+1)*tree3[i][j]+tree4[i][j];}}return ans;
}//范圍增加
void add(int a,int b,int c,int d,int v)
{add(a,b,v);add(a,d+1,-v);add(c+1,b,-v);add(c+1,d+1,v);
}//范圍查詢
int query(int a,int b,int c,int d)
{return sum(c,d)-sum(a-1,d)-sum(c,b-1)+sum(a-1,b-1);
}void solve()
{char type;int a,b,c,d,v;//一直讀取直到結尾while(scanf("%s",&type)!=EOF)//不能用%c -> 避免讀取回車或空格字符！{if(type=='X'){scanf("%d %d",&n,&m);}else if(type=='L'){scanf("%d %d %d %d %d",&a,&b,&c,&d,&v);add(a,b,c,d,v);}else{scanf("%d %d %d %d",&a,&b,&c,&d);printf("%d\n",query(a,b,c,d));}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

所以每次范圍增加時，要根據二維差分調用四次單點增加的函數，然后在單點增加的函數里，要先求出四個數組分別增加的值，然后循環增加四個數組的值。范圍查詢時就要根據二維前綴和調用四次從(1,1)到(n,m)的前綴和，然后在前綴和的函數里就是按照公式計算即可。

三、題目

1.逆序對

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=5e5+5;
vector<ll>arr(MAXN);
vector<ll>help(MAXN);//歸并排序輔助數組//歸并排序+合并左右答案
ll merge(int l,int m,int r)
{//統計答案ll ans=0;//i和j分別從左側和右側的最右位置開始for(int i=m,j=r;i>=l;i--){while(j>=m+1&&arr[i]<=arr[j]){j--;}//j右側均為可以和a[i]構成逆序對的數ans+=j-m;}//歸并排序int i=l;//填的位置//左右部分指針int a=l;int b=m+1;while(a<=m&&b<=r){help[i++]=arr[a]<=arr[b]?arr[a++]:arr[b++];}//填剩余的while(a<=m){help[i++]=arr[a++];}while(b<=r){help[i++]=arr[b++];}//重設arrfor(int i=l;i<=r;i++){arr[i]=help[i];}return ans;
}//l~r范圍上的逆序對數量
ll dfs(int l,int r)
{if(l==r){return 0;}int m=(l+r)/2;return dfs(l,m)+dfs(m+1,r)+merge(l,m,r);
}//歸并分治解
void solve1()
{int n;cin>>n;for(int i=0;i<n;i++){cin>>arr[i];}cout<<dfs(0,n-1)<<endl;
}//樹狀數組
vector<int>tree(MAXN);int lowbit(int i)
{return i&-i;
}void add(int i,int v,int n)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}//1~i的累加和
ll sum(int i)
{ll ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//查出現位置
int bs(int i,int m,vector<ll>&sorted)
{int l=1;int r=m;int mid;int ans=0;while(l<=r){mid=(l+r)/2;if(sorted[mid]>=i){ans=mid;r=mid-1;}else{l=mid+1;}}return ans;
}//樹狀數組解
void solve2()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>arr[i];}//樹狀數組維護詞頻數組//然后從后往前遍歷，邊統計詞頻邊統計答案//此時，樹狀數組的下標為數值 -> 值域樹狀數組//因為數字很大，所以要對其離散化vector<ll>sorted(n+1);for(int i=1;i<=n;i++){sorted[i]=arr[i];}sort(sorted.begin()+1,sorted.end());//去重int m=1;for(int i=2;i<=n;i++){if(sorted[m]!=sorted[i]){sorted[++m]=sorted[i];}}//二分for(int i=1;i<=n;i++){arr[i]=bs(arr[i],m,sorted);}//構建樹狀數組ll ans=0;for(int i=n;i>=1;i--){ans+=sum(arr[i]-1);add(arr[i],1,m);}cout<<ans;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve2();    }return 0;
}

這個題有歸并分治和樹狀數組兩個解。歸并分治的解比較好理解，但缺點是只能離線處理，沒法在線處理。樹狀數組的解雖然比較難想，但可以支持在線查詢。

歸并分治的解就比較好理解了，只需要在每次merge的過程中，設置雙指針滑一遍兩部分就能統計出答案，然后進行歸并排序即可。

代碼就是dfs返回l到r范圍上的逆序對數量，然后在merge的過程中，分別在左側和右側的最右位置設置兩個指針，只要右指針位置的數大于等于左指針位置的數，就讓右指針左移。由于歸并排序保證了左右兩側分別有序，所以此時從右指針到中間的所有數都小于左指針位置的數。所以此時左指針位置的數對答案的貢獻就是右指針到中間的數的個數。遍歷完一遍后歸并排序整合左右兩側即可。

樹狀數組的解比較需要思考了，這里考慮用樹狀數組維護詞頻數組。之后，考慮從后往前遍歷，每個數對答案的貢獻就是此時詞頻表中小于這個數的個數，那么就可以用樹狀數組實現在線查詢了。

要注意的是，由于樹狀數組維護的是詞頻表，所以下標代表的是實際數字，所以如果直接開整個數字范圍的長度，有可能導致空間過大。所以要考慮對數組進行離散化，方法是設置一個sorted數組，先把原數組抄過來，然后對其進行排序。之后，設置雙指針對排序后的數組進行去重，只提取數字的種類。最后，利用這個去重后的sorted數組，將原數組映射成大小排名，所以就是每次在sorted數組有效部分里二分找相同的數字的位置，然后用這個位置作為這個數字大小的排名建立詞頻表。這樣，就把規模由原來跟數字大小有關，轉化成了跟原數組長度有關。

所以代碼就是先把原數組抄到sorted數組里排序，接著進行去重。去重的方法就是設置m為有效區域的右邊界，注意，由于這里的下標對應樹狀數組的下標，所以m要從1開始計算。只要m位置的數不等于i位置的數，說明出現了一個不同的數，那就把m的下一個位置填成這個出現的新數。之后就是二分找原數組中的數的大小排名，再填回原數組。最后就是遍歷原數組，每次統計當前數對答案的貢獻，即小于等于當前數減一的詞頻之和。然后讓當前數的詞頻加一，在樹狀數組中修改即可。

2.三元上升子序列

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=3e4+5;
const int MAXV=1e5+5;//詞頻表的樹狀數組
vector<ll>cnts(MAXV);
//上升二元組的樹狀數組
vector<ll>two(MAXV);int lowbit(int i)
{return i&(-i);
}void add(int i,ll v,vector<ll>&tree)
{while(i<MAXV){tree[i]+=v;i+=lowbit(i);}
}ll sum(int i,vector<ll>&tree)
{ll ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}void solve()
{int n;cin>>n;vector<ll>a(n+1);for(int i=1;i<=n;i++){cin>>a[i];}//建立詞頻表 -> 上升一元組數量//建立以v結尾的上升二元組數量 -> 詞頻表的前綴和//以v結尾的上升三元組數量 -> 上升二元組數量的前綴和ll ans=0;for(int i=1;i<=n;i++){ans+=sum(a[i]-1,two);add(a[i],1,cnts);add(a[i],sum(a[i]-1,cnts),two);}cout<<ans;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

這個題的思路跟上一道很類似，首先還是建立一個詞頻表，含義可以理解為上升一元組數量，所以每次就在對應的位置加一即可。然后再建立一個以v結尾的上升二元組數量的數組，所以這個上升二元組每次就加上小于這個數的詞頻總數。所以對于每個數，對答案的貢獻就是上升二元組里小于這個數的個數。所以只需要分別對這個詞頻表和上升二元組建立兩個樹狀數組，之后這些信息就都可以快速查詢了。

3.最長遞增子序列的個數

class Solution {
public:int MAXN=2000+5;//離散化vector<int>sorted;//結尾值<=i的最長遞增子序列長度vector<int>treeMaxLen;//個數vector<int>treeMaxLenCnt;int m=0;int maxLen,maxLenCnt;void build(){sorted.resize(MAXN);treeMaxLen.resize(MAXN);treeMaxLenCnt.resize(MAXN);}int findNumberOfLIS(vector<int>& nums) {int n=nums.size();build();//樹狀數組維護以每個位置負責的數值結尾的情況下，//最長遞增子序列的長度和個數//e.g.tree[4]維護以1~4結尾的最長長度和對應個數//遍歷時更新 -> 按lowbit跳轉add//每次統計最長的個數 -> 按lowbit跳轉sum//離散化for(int i=1;i<=n;i++){sorted[i]=nums[i-1];}sort(sorted.begin()+1,sorted.begin()+n+1);m=1;for(int i=2;i<=n;i++){if(sorted[m]!=sorted[i]){sorted[++m]=sorted[i];}}//統計答案for(int num:nums){int i=rank(num);//查詢query(i-1);//之前的最大長度再往上沖一個//若之前的個數為0，說明只有自己，當前個數為1add(i,maxLen+1,max(maxLenCnt,1));}//m為最大值 -> 找以所有數值結尾的答案 -> 整體最長遞增子序列個數query(m);return maxLenCnt;}int lowbit(int i){return i&(-i);}//更新以<=i結尾的最長遞增子序列的長度和個數void add(int i,int len,int cnt){while(i<=m){if(treeMaxLen[i]==len)//沒法沖得更長{treeMaxLenCnt[i]+=cnt;}else if(treeMaxLen[i]<len)//能沖得更長{treeMaxLen[i]=len;treeMaxLenCnt[i]=cnt;}i+=lowbit(i);}}//查詢以<=i結尾的最長遞增子序列的長度和個數void query(int i){//全局變量返回兩個值maxLen=maxLenCnt=0;while(i>0){if(maxLen==treeMaxLen[i])//沒法沖得更長{maxLenCnt+=treeMaxLenCnt[i];}else if(maxLen<treeMaxLen[i])//能沖得更長{maxLen=treeMaxLen[i];maxLenCnt=treeMaxLenCnt[i];}i-=lowbit(i);}}//查詢排名int rank(int v){int l=1;int r=m;int mid;int ans=0;while(l<=r){mid=(l+r)/2;if(sorted[mid]>=v){ans=mid;r=mid-1;}else{l=mid+1;}}return ans;}
};

這個題的思路也比較難想。

思路就是用兩個樹狀數組分別維護以小于等于v這個數結尾的最長遞增子序列的長度和個數。之后，每次查詢或增加時，都利用樹狀數組O(logn)的時間遍歷1~i的方法，去根據lowbit跳轉。

在查詢時，因為要返回最長長度和對應個數兩個值，所以考慮用全局變量實現。在跳轉過程中，如果之前的值的最長遞增子序列的長度等于當前的最長長度，那么此時的長度就要加上小于等于當前i的最長遞增子序列的個數。如果當前的最長遞增子序列的長度比目前的最長長度更長，那么當前的數就能踩在之前的最長遞增子序列上更新得更長，所以就更新當前的maxLen和maxLenCnt即可。

查詢完以小于當前數結尾的最長遞增子序列的長度和個數后，當前數就可以踩在上面把這個長度更新得更長，那就是maxLen再加一。這里注意，如果查出來的個數為0，說明當前數只能自己一個，所以maxLenCnt還要和1取一個最大值。之后更新時，還是按lowbit跳轉更新之前的maxLen和maxLenCnt。如果之前的長度等于len時，那么就沒法借助當前數沖得更長，那就只增加個數。如果小于，那么說明可以變得更長，那就更新兩個樹狀數組即可。

注意，由于這里樹狀數組的下標還是代表實際數字，所以還是需要對原數組進行離散化。

4.HH的項鏈

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=1e6+5;//樹狀數組維護區間內顏色出現的最右位置 -> 0：沒出現過 1：出現過
vector<int>tree(MAXN);int lowbit(int i)
{return i&(-i);
}void add(int i,int v,int n)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}int sum(int i)
{int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}int query(int l,int r)
{return sum(r)-sum(l-1);
}void solve()
{int n;scanf("%d",&n);vector<int>a(n+1);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}int m;scanf("%d",&m);vector<array<int,3>>q(m);for(int i=0;i<m;i++){scanf("%d%d",&q[i][0],&q[i][1]);q[i][2]=i;}//根據查詢的右邊界從小到大排序sort(q.begin(),q.end(),[&](const array<int,3>&x,const array<int,3>&y){return x[1]<y[1];});//map維護每種顏色出現的最右位置map<int,int>right;//答案vector<int>ans(m);for(int i=0,cur=1,l,r,fill;i<m;i++){//右邊界r=q[i][1];//每次遍歷到右邊界for(;cur<=r;cur++){int color=a[cur];//該顏色以前出現過if(right[color]>0){//將舊位置上的標記去掉add(right[color],-1,n);}//在新位置標記add(cur,1,n);right[color]=cur;}l=q[i][0];fill=q[i][2];ans[fill]=query(l,r);}for(int i=0;i<m;i++){printf("%d\n",ans[i]);}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

nnd這題還必須用快讀快寫。

這題的思路也是很逆天了……首先，考慮對要查詢的區間按右邊界從小到大排序。但由于這會破壞原始查詢的順序，所以還要帶著次序信息排序。之后，考慮建立一個map維護每種顏色出現的最右位置，再用樹狀數組維護一個區間內的顏色出現的最右位置。這里，tree[i]如果是1，就表示存在一種顏色的最右位置為i。

舉個例子，假如此時的tree為[1,1,1,0]，而原數組為[3,1,2,3]，當前遍歷到3位置。那么當來到4位置時，此時3號顏色最右出現的位置就不是1位置，而是4位置了。那么就需要將tree更新為[0,1,1,1]，表示當前不再存在一種顏色的最右位置為1位置。

所以就是遍歷所有的查詢，每次在原數組中遍歷到當前查詢的最右邊界。在遍歷原數組的過程中，如果當前顏色以前出現過，那么需要先在樹狀數組中把之前位置的1減去，然后在新位置打上標記。最后，只需要求當前查詢區間的累加和就是其中不同的顏色的種類數。

這個思路的核心就是，通過只保留最右出現的位置，來實現同種顏色不重復統計。也是因為這一點，所以可以對查詢的最右邊界排序，這樣在遍歷原數組的過程中就能統計出答案。

5.得到回文串的最少操作次數

力扣的比賽這么逆天的嗎……這題感覺沒個幾年的功力根本不可能寫得出來……

class Solution {
public:const int MAXN=2000+5;//樹狀數組vector<int>tree;int n;//每個字符的出現位置 -> 鏈式前向星vector<int>ends;//最后出現的位置vector<int>pre;//之前出現的位置//每個字符應該去的位置vector<int>pos;//歸并分治輔助數組vector<int>help;void build(){tree.resize(MAXN);pos.resize(MAXN);help.resize(MAXN);for(int i=1;i<=n;i++){//樹狀數組每個位置標記為1add(i,1);}ends.resize(26);pre.resize(MAXN);}int minMovesToMakePalindrome(string s) {n=s.length();build();//貪心：//從左往右遍歷時，每次可以先滿足當前位置的字符為回文//e.g. aaaabb -> a????a -> aa??aa -> aabbaa//關鍵：相鄰交換！左側往左交換過去時會把中間字符串擠過來//e.g. stXtYtYtXts -> 先滿足X -> XsttYtYttsX -> XYstttttsYX -> (2+2)+(3+3)=10//                    先滿足Y -> YstXtttXtsY -> YXstttttsYX -> (4+4)+(2+2)=12for(int i=0,j=1;i<n;i++,j++){//和樹狀數組有關，下標從1開始push(s[i]-'a',j);}for(int i=0,l=1,r,fill;i<n;i++,l++){//沒分配位置if(pos[l]==0){//最后出現的位置r=pop(s[i]-'a');if(l<r)//這個字符剩不止一個{//應該去的位置fill=sum(l);pos[l]=fill;pos[r]=n-fill+1;//對稱位置}else//只剩一個 -> 必在中間{pos[l]=(n+1)/2;}//去掉標簽add(r,-1);}}//對pos求逆序對return number(1,n);}//統計字符出現位置void push(int v,int j){pre[j]=ends[v];ends[v]=j;}//每個字符的最后下標int pop(int v){int ans=ends[v];ends[v]=pre[ends[v]];return ans;}int lowbit(int i){return i&(-i);}void add(int i,int v){while(i<=n){tree[i]+=v;i+=lowbit(i);}}int sum(int i){int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;}//歸并分治求逆序對數量int number(int l,int r){if(l>=r){return 0;}int m=(l+r)/2;return number(l,m)+number(m+1,r)+merge(l,m,r);}//歸并排序+合并左右答案int merge(int l,int m,int r){//統計答案int ans=0;//i和j分別從左側和右側的最右位置開始for(int i=m,j=r;i>=l;i--){while(j>=m+1&&pos[i]<=pos[j]){j--;}//j右側均為可以和a[i]構成逆序對的數ans+=j-m;}//歸并排序//填的位置int i=l;//左右部分指針int a=l;int b=m+1;while(a<=m&&b<=r){help[i++]=pos[a]<=pos[b]?pos[a++]:pos[b++];}//填剩余的while(a<=m){help[i++]=pos[a++];}while(b<=r){help[i++]=pos[b++];}//重設arrfor(int i=l;i<=r;i++){pos[i]=help[i];}return ans;}
};

這題的突破點其實需要貪心一下，那就是在從左往右遍歷的過程中，可以先讓當前來到的位置滿足回文結構。舉個例子，假如原串是aaaabb，那么在從左往右遍歷時，可以先構成a????a，再構成aa??aa，最后aabbaa即可。具體原理如注釋里寫的，就是在左側字符向左移動時，可以把左邊的字符串擠過去，這樣當更右側的字符向左移動時，就不用經過那個已經移過去的字符了。

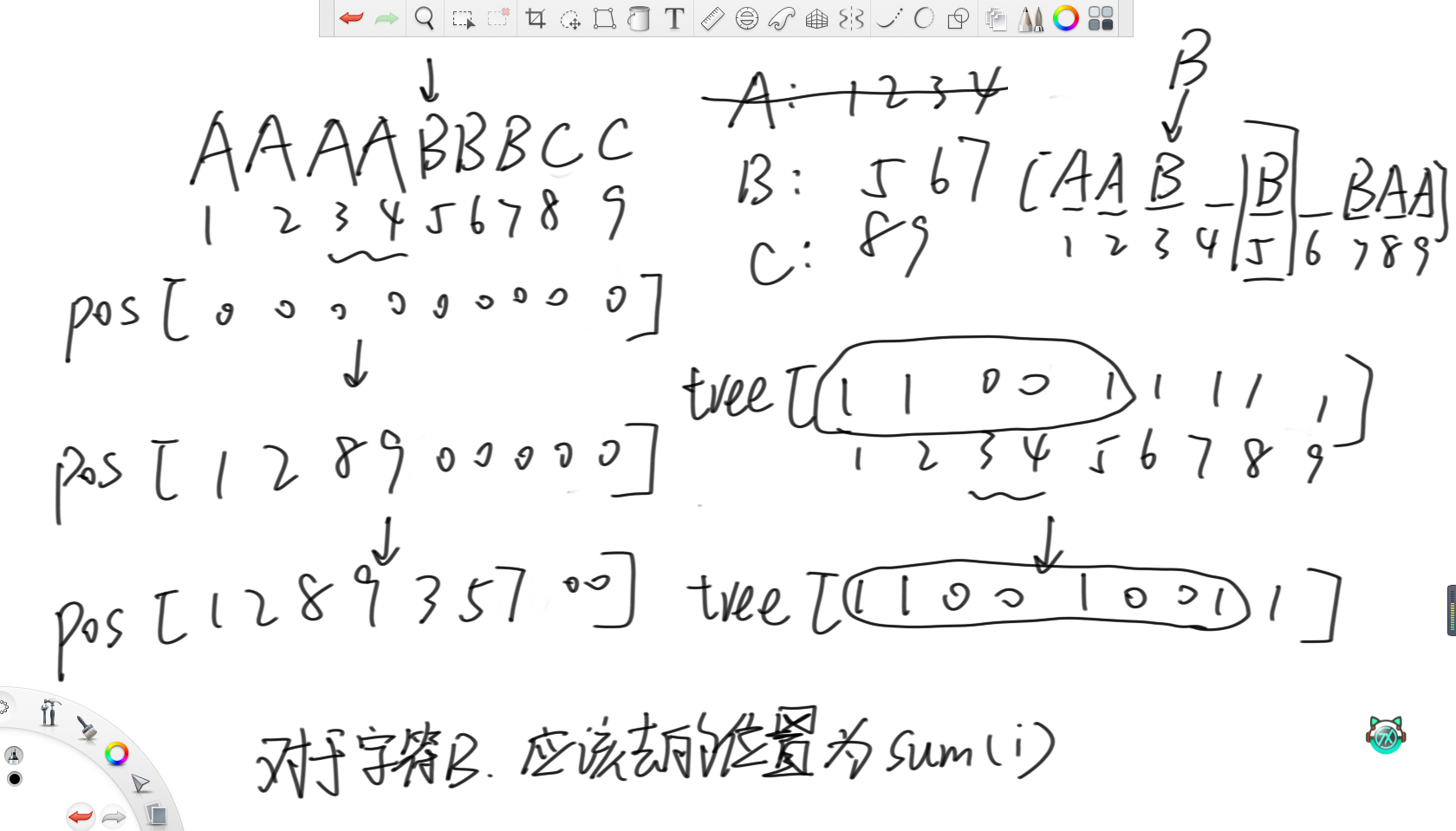
之后，考慮建立pos數組，表示每個位置的字符應該去的位置。之后，用樹狀數組維護哪個位置的字符被移動走了，初始每個位置都是1。那么對于每個來到的字符，其應該去的位置就是樹狀數組中1~i的前綴和。由于將一個字符移到了左側，所以考慮將最右出現的這個字符移到右側去，然后在樹狀數組中將這個被移走了的字符的位置改為0。

在上面例子中，當來到第一個A，應該去的位置就是樹狀數組中1~1上的累加和，那就是1位置。然后最右4位置的A移到9位置，然后把樹狀數組的4位置從1改成0。第二個A類似。當來到第一個B時，應該去的位置為樹狀數組1~5的累加和，那就是3位置。然后把7位置的B移到7位置，樹狀數組的7位置改成0。之后，由于B只剩一個，所以必然要去整個字符串的中點位置。之后C字符以此類推。

當求出pos數組后，觀察可得，此時pos數組的次序對數量就是需要移動的次數。在上面例子中，從右往左看，可以寫出所有的逆序對。所以移動的方法就是，先處理以9開頭的逆序對，那就是將4位置的A移動到9位置。之后，讓3位置的A移動到8位置。最后讓7位置的B移動回7位置，再讓6位置的B移動5位置即可。

雖然這個位置表第一眼看上去很像鄰接表，但由于要每次取某個字符最右出現的位置，所以這里用了一種類似鏈式前向星的方式構建。方法就是設置ends數組和pre數組，ends數組存每個字符最右出現的位置，之后根據pre往前跳就是之前出現的位置。那么要取最右位置只需要從ends里取，然后把ends更新成跳去的pre里的值即可。