python版PCA(主成分分析)??
在用統計分析方法研究這個多變量的課題時,變量個數太多就會增加課題的復雜性。人們自然希望變量個數
較少而得到的信息較多。在很多情形,變量之間是有一定的相關關系的,當兩個變量之間有一定相關關系時,可
以解釋為這兩個變量反映此課題的信息有一定的重疊。主成分分析是對于原先提出的所有變量,建立盡可能少的
新變量,使得這些新變量是兩兩不相關的,而且這些新變量在反映課題的信息方面盡可能保持原有的信息。
綜合變量盡可能多地反映原來變量的信息的統計方法叫做主成分分析或稱主分量分析,也是數學上處理降維的一
較少而得到的信息較多。在很多情形,變量之間是有一定的相關關系的,當兩個變量之間有一定相關關系時,可
以解釋為這兩個變量反映此課題的信息有一定的重疊。主成分分析是對于原先提出的所有變量,建立盡可能少的
新變量,使得這些新變量是兩兩不相關的,而且這些新變量在反映課題的信息方面盡可能保持原有的信息。
原理
設法將原來變量重新組合成一組新的互相無關的幾個綜合變量,同時根據實際需要從中可以取出幾個較少的綜合變量盡可能多地反映原來變量的信息的統計方法叫做主成分分析或稱主分量分析,也是數學上處理降維的一
種方法。
步驟
主成分分析主要步驟如下:
- 指標數據標準化;
- 指標之間的相關性判定;
- 計算特征值與特征向量
- 計算主成分貢獻率及累計貢獻率
- 計算主成分載荷
代碼
[python]?view plaincopy

- #-*-?coding:utf-8?-*-??
- from?pylab?import?*??
- from?numpy?import?*??
- ??
- def?pca(data,nRedDim=0,normalise=1):??
- ????#?數據標準化??
- ????m?=?mean(data,axis=0)??
- ????data?-=?m??
- ????#?協方差矩陣??
- ????C?=?cov(transpose(data))??
- ????#?計算特征值特征向量,按降序排序??
- ????evals,evecs?=?linalg.eig(C)??
- ????indices?=?argsort(evals)??
- ????indices?=?indices[::-1]??
- ????evecs?=?evecs[:,indices]??
- ????evals?=?evals[indices]??
- ????if?nRedDim>0:??
- ????????evecs?=?evecs[:,:nRedDim]??
- ??
- ????if?normalise:??
- ????????for?i?in?range(shape(evecs)[1]):??
- ????????????evecs[:,i]?/?linalg.norm(evecs[:,i])?*?sqrt(evals[i])??
- ????#?產生新的數據矩陣??
- ????x?=?dot(transpose(evecs),transpose(data))??
- ????#?重新計算原數據??
- ????y=transpose(dot(evecs,x))+m??
- ????return?x,y,evals,evecs??
- ??
- x?=?random.normal(5,.5,1000)??
- y?=?random.normal(3,1,1000)??
- ??
- a?=?x*cos(pi/4)?+?y*sin(pi/4)??
- b?=?-x*sin(pi/4)?+?y*cos(pi/4)??
- ??
- plot(a,b,'.')??
- ??
- xlabel('x')??
- ylabel('y')??
- ??
- title('raw?dataset')??
- ??
- data?=?zeros((1000,2))??
- data[:,0]?=?a??
- data[:,1]?=?b??
- x,y,evals,evecs?=?pca(data,1)??
- print?y??
- figure()??
- plot(y[:,0],y[:,1],'.')??
- xlabel('x')??
- ylabel('y')??
- title('new?dataset')??
- show()??
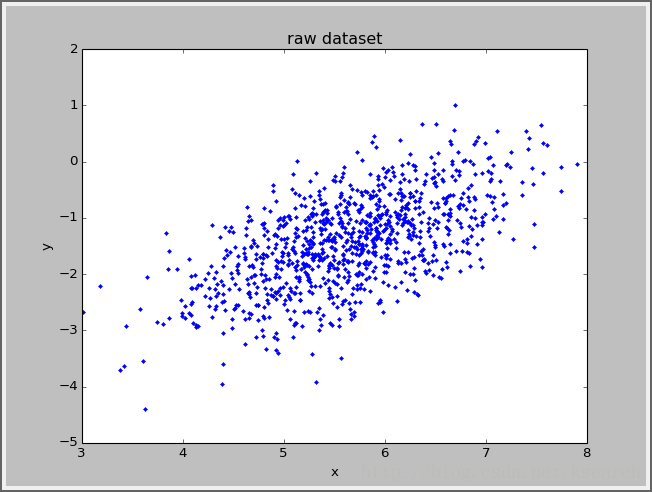
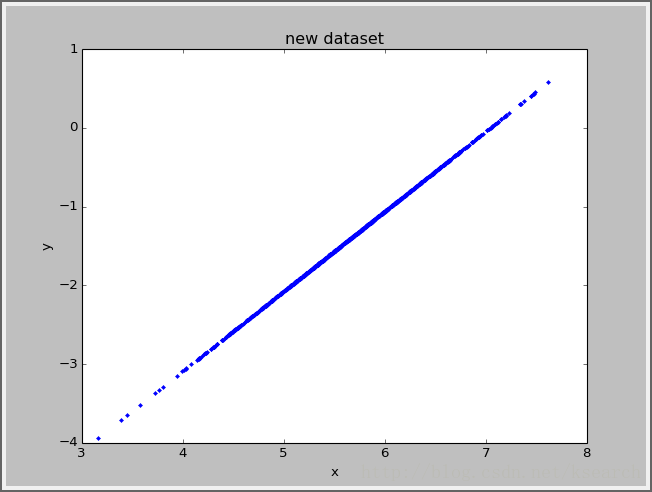
效果




詳解)






函數與緩沖區)




)

(一))


 Exception)