👨?🎓作者簡介：一位即將上大四，正專攻機器學習的保研er
🌌上期文章：機器學習&&深度學習——seq2seq實現機器翻譯（詳細實現與原理推導）
📚訂閱專欄：機器學習&&深度學習
希望文章對你們有所幫助

引入

上一節已經實現了機器翻譯的模型訓練和預測，逐個預測輸出序列， 直到預測序列中出現特定的序列結束詞元eos，而對于預測序列的結果我們進行了評估，發現了效果并不好。因為之前的方式是使用了貪心搜索方式，這個搜索方式并不能使得全局上是優秀的，甚至是非常差的。接下來將介紹搜索方式。
我們已經知道，在任意的時間步，解碼器的輸出的概率取決于時間步之前的輸出子序列和對輸入序列的信息進行編碼得到的上下文變量。為了量化計算代價，用γ表示輸出詞表（包含eos），而|γ|顯然就是詞表大小。
除此之外，我們限制一下輸出序列的最大詞元數T^’。

貪心搜索

對于輸出序列的每一個時間步t^’，我們都將基于貪心搜索從γ中找到具有最高條件概率的詞元，即：
$$y_{t^{{}^{\prime }}}=argma{x}_{y\in \gamma }P(y|y_1,...,y_{t^{{}^{\prime }}?1},c)$$
一旦輸出序列包含了eos或者已經達到了最大長度T^’，則輸出完成。

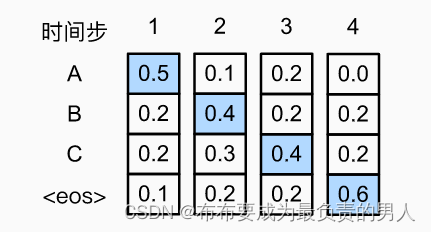
上圖中的預測輸出序列是ABC和eos，這個輸出序列的條件概率就是0.5×0.4×0.4×0.6=0.048。
而如果我們在第二個時間步換一下，換成C，那么可能AC后面跟著的A、B、C和eos的概率就會全變了，例如：

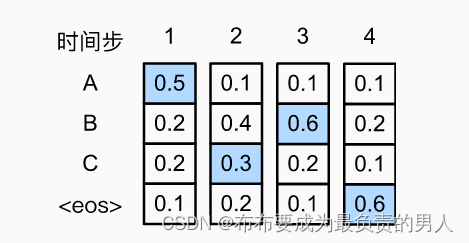
計算得出輸出序列ACB和eos的條件概率為0.054，大于之前的貪心方式得到的結果。搞過動態規劃算法的朋友們都知道貪心就是很可能出現這種情況，所以貪心搜索本身就不是一個很好的搜索策略。

窮舉搜索

這個好理解，就是所有結果全部遍歷過去，這樣的話，我們絕對可以找到條件概率最高的一個。然而這樣的復雜度將會非常的大，計算量會達到：
$$O(|\gamma {|}^{T^{{}^{\prime }}})$$
因此在詞元數過多，或者預測序列的最大詞元數太大的話，這個方法簡直是非常的慢。

束搜索

顯然，上面的可以得出一個簡單的選擇策略：如果精度最重要，則顯然是窮舉搜索；如果計算成本最重要，則顯然是貪心搜索。而束搜索則是介于兩者之間的（算是貪心的一個改進版本）。
它有一個超參數，名為束寬，記為k。在每個時間步，我們都選擇具有最高條件概率的k個詞元，過程如下所示（束寬為2，最大長度為3）：

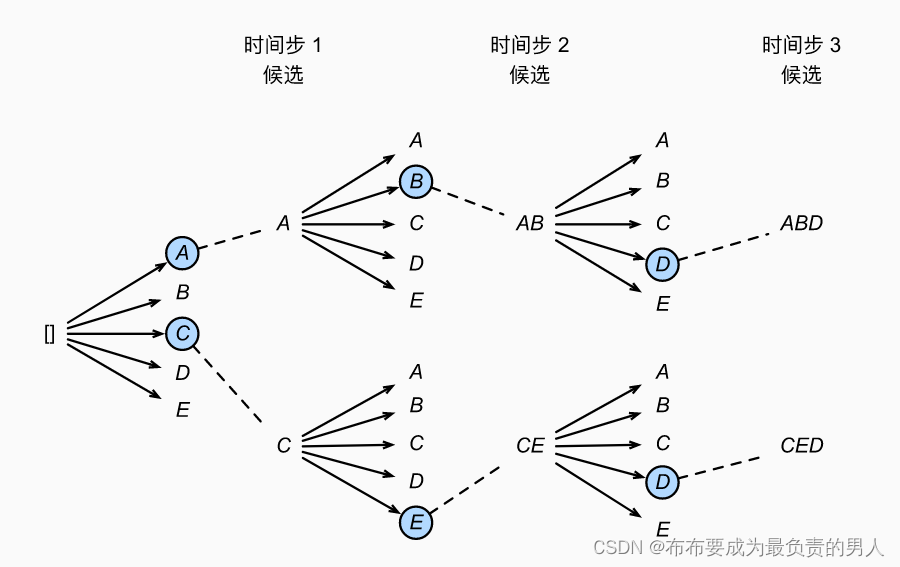
我們從這里面選出六個候選輸出序列：
（1）A；（2）C；（3）AB；（4）CE；（5）ABD；（6）CED
最后基于這六個序列， 我們獲得最終候選輸出序列集合。然后我們選擇其中條件概率乘積最高的序列作為輸出序列：
$$\frac{1}{L^{\alpha }}logP(y_1,...,y_L|c)=\frac{1}{L^{\alpha }}\sum _{t^{{}^{\prime }}=1}^{L}logP(y_{t^{{}^{\prime }}}|y_1,...,y_{t^{{}^{\prime }}?1},c)$$
其中，L是最終候選序列的長度，α通常設為0.75。這樣做是因為，一個較長的序列在求和中會有更多的對數項，因此分母用來懲罰長序列。
實際上，貪心搜索就可以看作是一種束寬為1的特殊類型的束搜索。束搜索可以在正確率和計算代價之間進行權衡。

小結

1、序列搜索策略包括貪心搜索、窮舉搜索和束搜索。
2、貪心搜索所選取序列的計算量最小，但精度相對較低。
3、窮舉搜索所選取序列的精度最高，但計算量最大。
4、束搜索通過靈活選擇束寬，在正確率和計算代價之間進行權衡。