1 支持向量機
1.1 故事引入
-
看下圖左邊,藍色和紅色的點混在一起,這就像一堆數據,沒辦法用一條簡單的直線把它們分開。再看下圖右邊,有一條直線把藍色和紅色的點分開,這就是SVM在找的“決策邊界”,它能把不同類別的數據分開。SVM的目標就是找到這樣一條線,讓不同類別的數據分得最開;

-
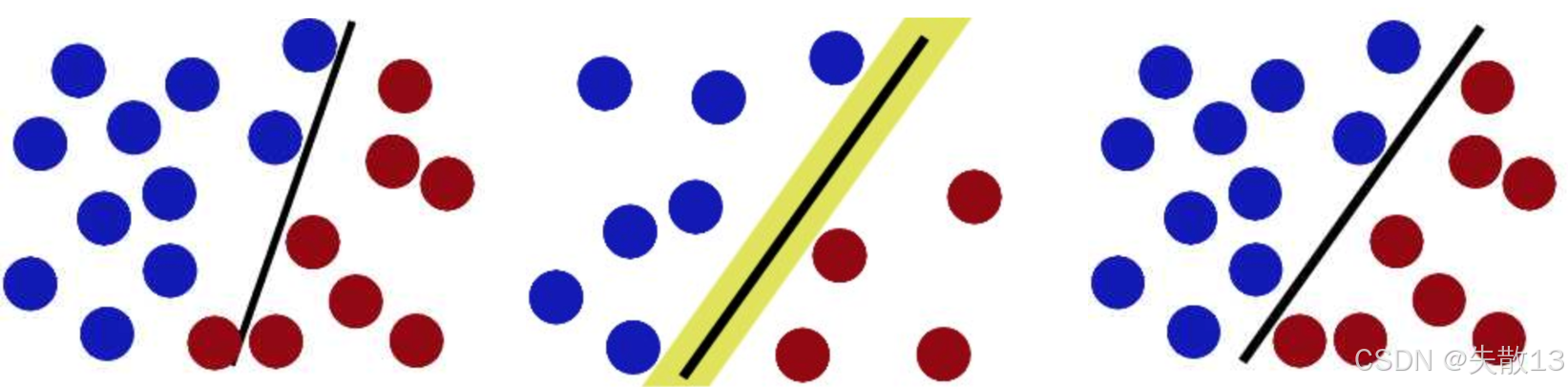
下圖有三條線;
- 左邊的線,離藍色和紅色的點都太近,這樣分類效果肯定不好,新的數據一來可能就會分錯;
- 中間那條線,周圍有個黃色的區域,這代表“間隔”,SVM要找的就是間隔最大的那條線,這樣分類才最穩定;
- 右邊那條線就是間隔最大的,它離兩邊的點都最遠,分類效果最好,這就是SVM的核心思想——最大化間隔;
-
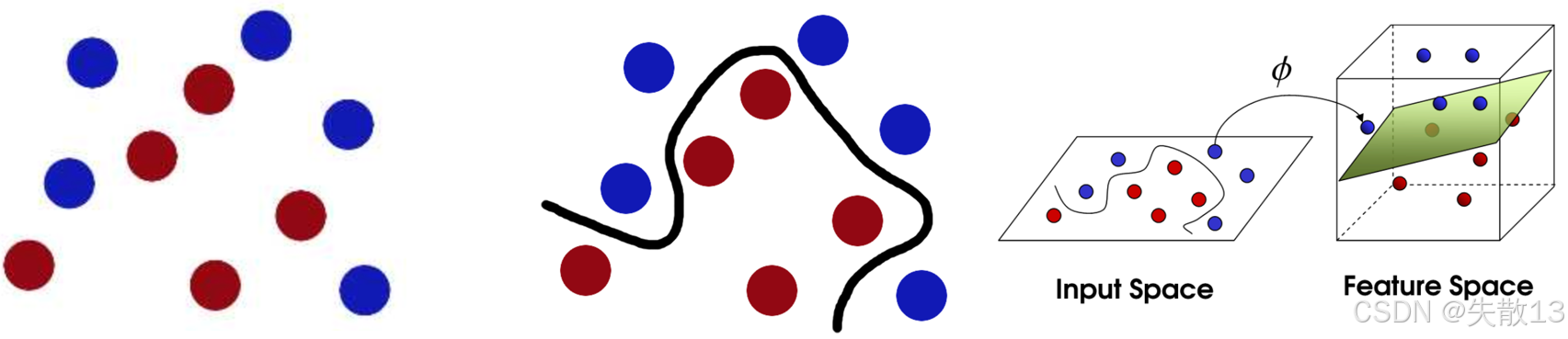
對于下面的三張圖:
- 左圖,藍色和紅色的點在一個平面上怎么都分不開,就像數據在低維度下沒辦法分類;
- 在中間的圖中,有一條曲線把它們分開了,這說明有時候得用曲線或者高維度的方式來分類;
- 右圖,它展示了SVM怎么把低維度的“輸入空間”(Input Space)通過一個函數 φ 映射到高維度的“特征空間”(Feature Space);
- 在高維度空間里,原本分不開的點就能用一個平面(超平面)分開;
- 這就是SVM的“核技巧”,不用真的計算高維度的點,而是通過核函數來計算點之間的關系;
1.2 概述
-
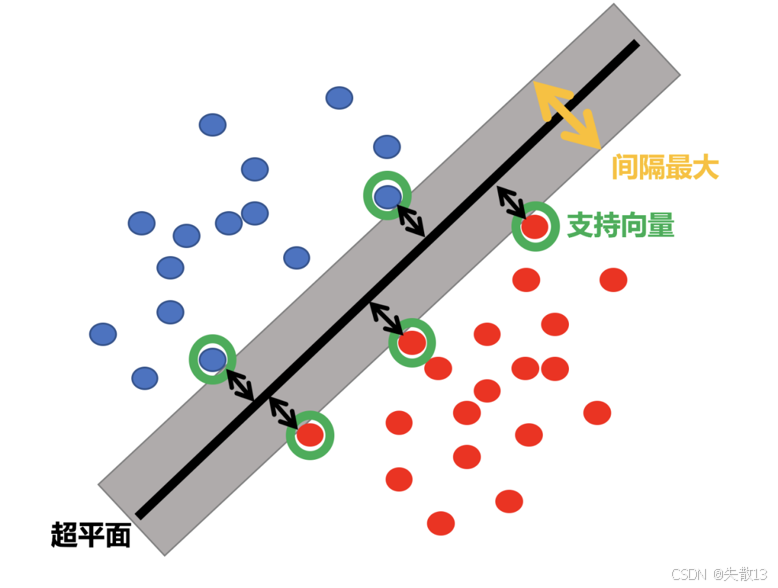
**支持向量機(SVM)**的目標是找到一個超平面,將數據樣本分成兩類,并且使得這兩類之間的間隔最大;
- 下圖中的黑色實線就是這個超平面,而兩側的虛線則表示間隔的邊界;
- 綠色圓圈標記的點是支持向量,這些點是離超平面最近的樣本點,對確定超平面的位置起到關鍵作用;
- 間隔越大,分類器的泛化能力通常越好,因為它對新數據的分類更穩定;
-
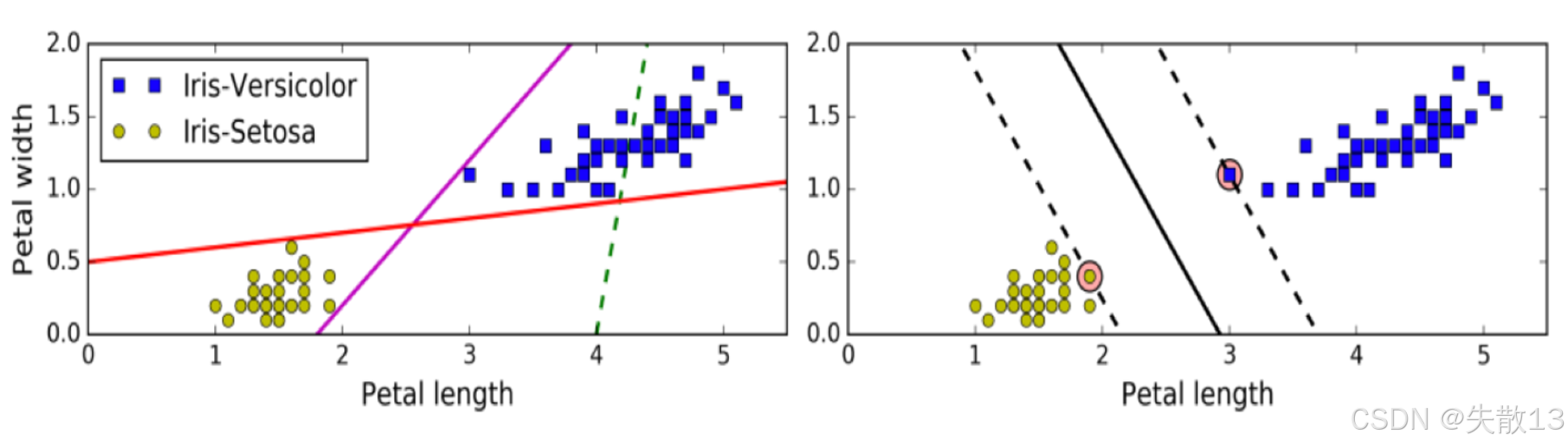
下圖比較了不同的分類超平面;
- 左邊的圖顯示了一些可能的分類線,但這些線并沒有最大化間隔;
- 右邊的圖則展示了 SVM 找到的最大間隔超平面。可以看到,SVM 的超平面離兩類樣本的距離最遠,這樣可以在分類時提供更好的容錯能力;
-
硬間隔要求所有樣本都必須被正確分類,并且在分類正確的情況下尋找最大間隔。然而,如果數據中存在異常值(Outlier)或者樣本本身線性不可分,硬間隔就無法實現。左邊的圖顯示了一個異常值導致無法找到硬間隔的情況,而右邊的圖則顯示了即使存在異常值,SVM 仍然嘗試找到一個合理的超平面;
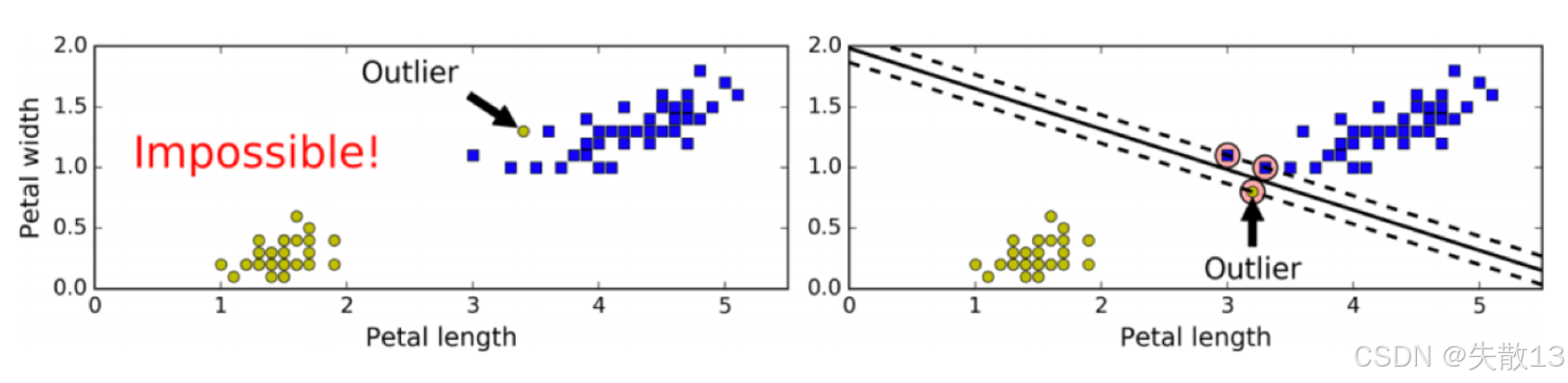
-
軟間隔允許部分樣本在最大間隔之內,甚至在錯誤的一邊,以尋找最大間隔。目標是在保持間隔寬闊和限制間隔違例之間找到平衡;
- 懲罰系數 C 控制這個平衡:C 值越小,間隔越寬,但允許的間隔違例越多;C 值越大,間隔越窄,但對間隔違例的懲罰越重;
- 左邊的圖顯示了 C=100 時的情況,間隔較窄,違例較少;右邊的圖顯示了 C=1 時的情況,間隔較寬,違例較多;
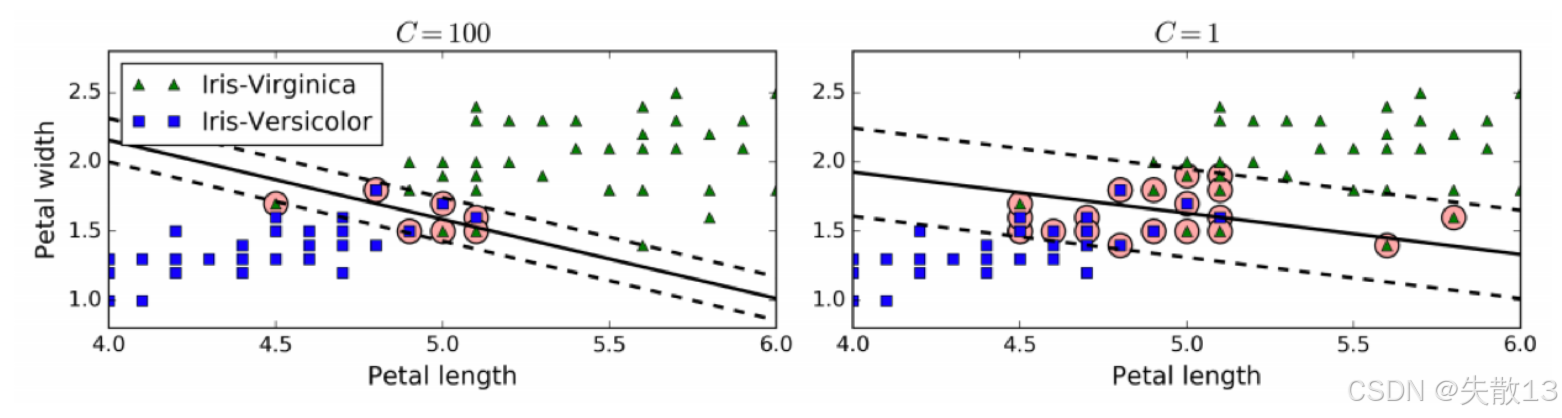
-
**核函數(Kernel)**將原始輸入空間映射到新的特征空間,使得原本線性不可分的樣本在新的特征空間中變得線性可分;
- 左邊的圖顯示了原始空間中線性不可分的樣本,右邊的圖顯示了通過核函數映射到新特征空間后,樣本變得線性可分,并且可以找到一個決策表面(Decision surface)來分隔兩類樣本;
- 常用的核函數包括線性核、多項式核、徑向基函數(RBF)核等;
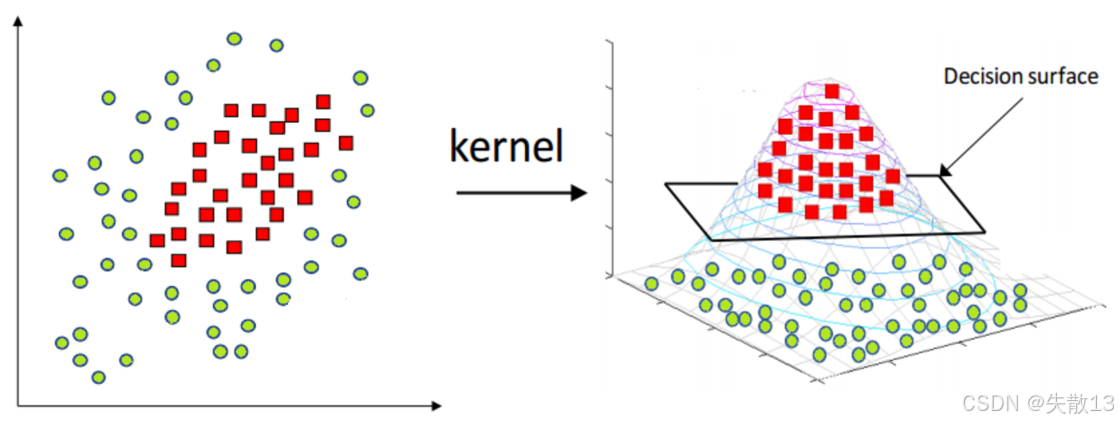
2 API&案例
2.1 API介紹
-
簡介:
class sklearn.svm.LinearSVC(C=1.0)-
庫/框架:
scikit-learn(通常簡稱為sklearn),這是一個常用的Python機器學習庫; -
類:
sklearn.svm.LinearSVC,這是scikit-learn庫中用于線性支持向量分類的類; -
C:懲罰系數,類似于線性回歸中的正則化系數。C值越大,模型對誤分類的懲罰越重,模型越傾向于正確分類每個樣本,但可能會導致過擬合;C值越小,模型對誤分類的懲罰越輕,模型可能更簡單,但可能會導致欠擬合;
-
-
示例代碼:
# 從sklearn.svm模塊中導入LinearSVC類 from sklearn.svm import LinearSVC # 創建LinearSVC類的實例,設置懲罰系數C為30 mysvc = LinearSVC(C=30) # 使用訓練數據X_standard和對應的標簽y來訓練模型 mysvc.fit(X_standard, y) # 輸出模型在訓練數據上的準確率 print(mysvc.score(X_standard, y))
2.2 案例:使用LinearSVC進行鳶尾花分類
-
自定義的決策邊界繪制工具:
import numpy as np import matplotlib.pyplot as pltdef plot_decision_boundary(model,axis):x0,x1 = np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))X_new = np.c_[x0.ravel(),x1.ravel()]y_predict = model.predict(X_new)zz = y_predict.reshape(x0.shape)from matplotlib.colors import ListedColormapcustom_map = ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])# plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)plt.contourf(x0,x1,zz,cmap=custom_map)def plot_decision_boundary_svc(model,axis):x0,x1 = np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))X_new = np.c_[x0.ravel(),x1.ravel()]y_predict = model.predict(X_new)zz = y_predict.reshape(x0.shape)from matplotlib.colors import ListedColormapcustom_map = ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])# plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)plt.contourf(x0,x1,zz,cmap=custom_map)w= model.coef_[0]b = model.intercept_[0]# w0* x0 + w1* x1+ b = 0#=>x1 = -w0/w1 * x0 - b/w1plot_x = np.linspace(axis[0],axis[1],200)up_y = -w[0]/w[1]* plot_x - b/w[1]+ 1/w[1]down_y = -w[0]/w[1]* plot_x - b/w[1]-1/w[1]up_index =(up_y >= axis[2])&(up_y <= axis[3])down_index =(down_y>= axis[2])&(down_y<= axis[3])plt.plot(plot_x[up_index],up_y[up_index],color="black")plt.plot(plot_x[down_index],down_y[down_index],color="black") -
導包:
from sklearn.datasets import load_iris # 加載鳶尾花數據集 import matplotlib.pyplot as plt from sklearn.preprocessing import StandardScaler from sklearn.svm import LinearSVC # 導入線性支持向量機分類器 from sklearn.metrics import accuracy_score # 用于計算模型準確率 from plot_util import plot_decision_boundary # 導入自定義的決策邊界繪制工具 -
加載數據:
# 1.加載數據 # 加載鳶尾花數據集,return_X_y=True表示分別返回特征數據和標簽 X,y=load_iris(return_X_y=True)print(y.shape) # (150,)。150個樣本 print(X.shape) # (150, 4)。每個樣本4個特征 # 為了簡化問題,只選取標簽為0和1的樣本(前兩類鳶尾花),且只使用前兩個特征 x = X[y<2,:2] # 取y<2的樣本,且只保留前兩個特征 y = y[y<2] # 相應的標簽也只保留y<2的部分 print(y.shape) # 輸出 (100,)。 前兩類各50個# 繪制標簽為0的樣本,用紅色表示 plt.scatter(x[y==0,0],x[y==0,1],c='red') # 繪制標簽為1的樣本,用藍色表示 plt.scatter(x[y==1,0],x[y==1,1],c='blue') plt.show()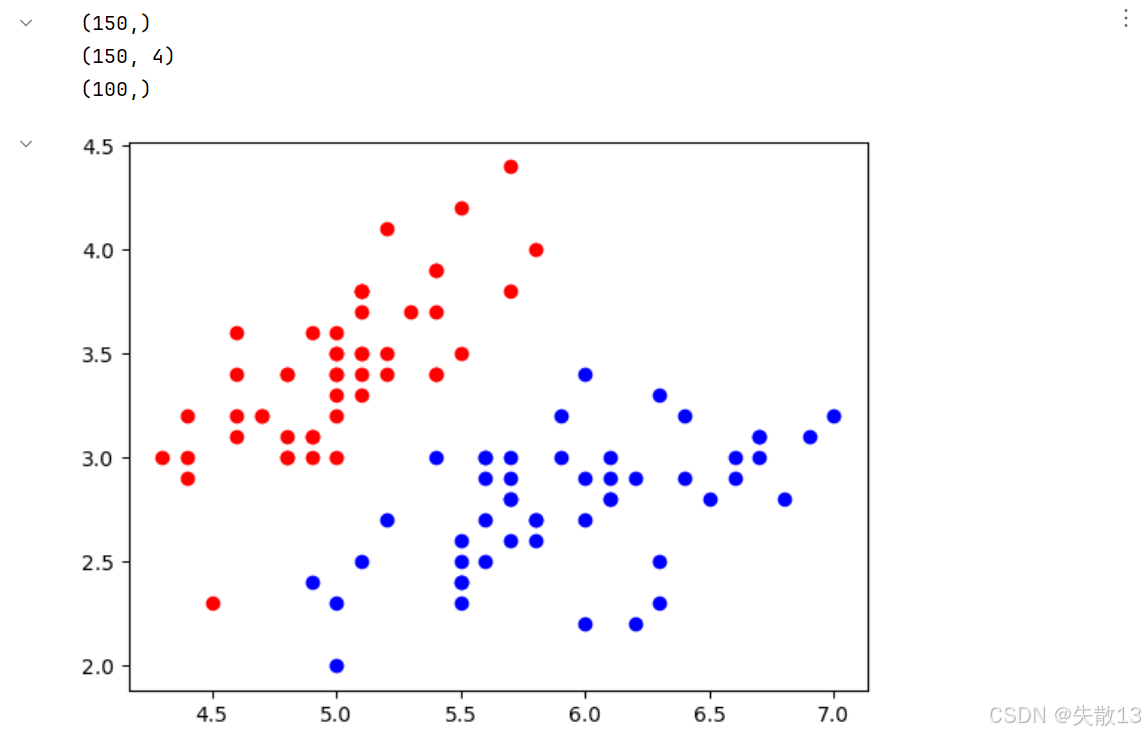
-
數據的預處理:
# 2.數據的預處理 # 創建標準化轉換器,將數據轉換為均值為0,標準差為1的標準正態分布 transform = StandardScaler() # 對特征數據進行擬合和轉換,計算均值和標準差并應用到數據上 x_tran = transform.fit_transform(x) -
模型訓練:
# 3.模型訓練 # 創建線性支持向量機分類器實例,設置懲罰系數C為10 # C值越大,對誤分類的懲罰越重,模型可能更復雜,容易過擬合 model=LinearSVC(C=10) model.fit(x_tran,y) y_pred = model.predict(x_tran)# 計算并打印模型在訓練數據上的準確率 # 準確率 = 正確預測的樣本數 / 總樣本數 print(accuracy_score(y_pred,y)) # 通常會接近1.0,因為是在訓練數據上評估
-
可視化:
# 4.可視化 # 繪制模型的決策邊界,axis參數指定了坐標軸的范圍 plot_decision_boundary(model,axis=[-3,3,-3,3]) # 在決策邊界圖上繪制標簽為0的標準化樣本點,紅色表示 plt.scatter(x_tran[y == 0, 0], x_tran[y == 0, 1], c='red') # 在決策邊界圖上繪制標簽為1的標準化樣本點,藍色表示 plt.scatter(x_tran[y==1,0],x_tran[y==1,1],c='blue') plt.show()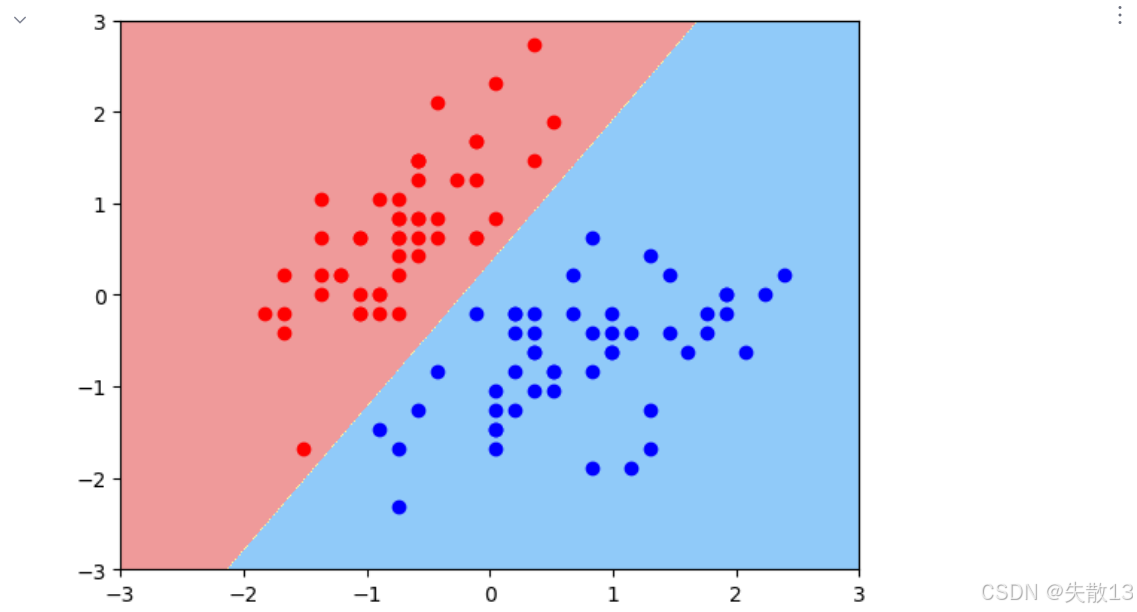
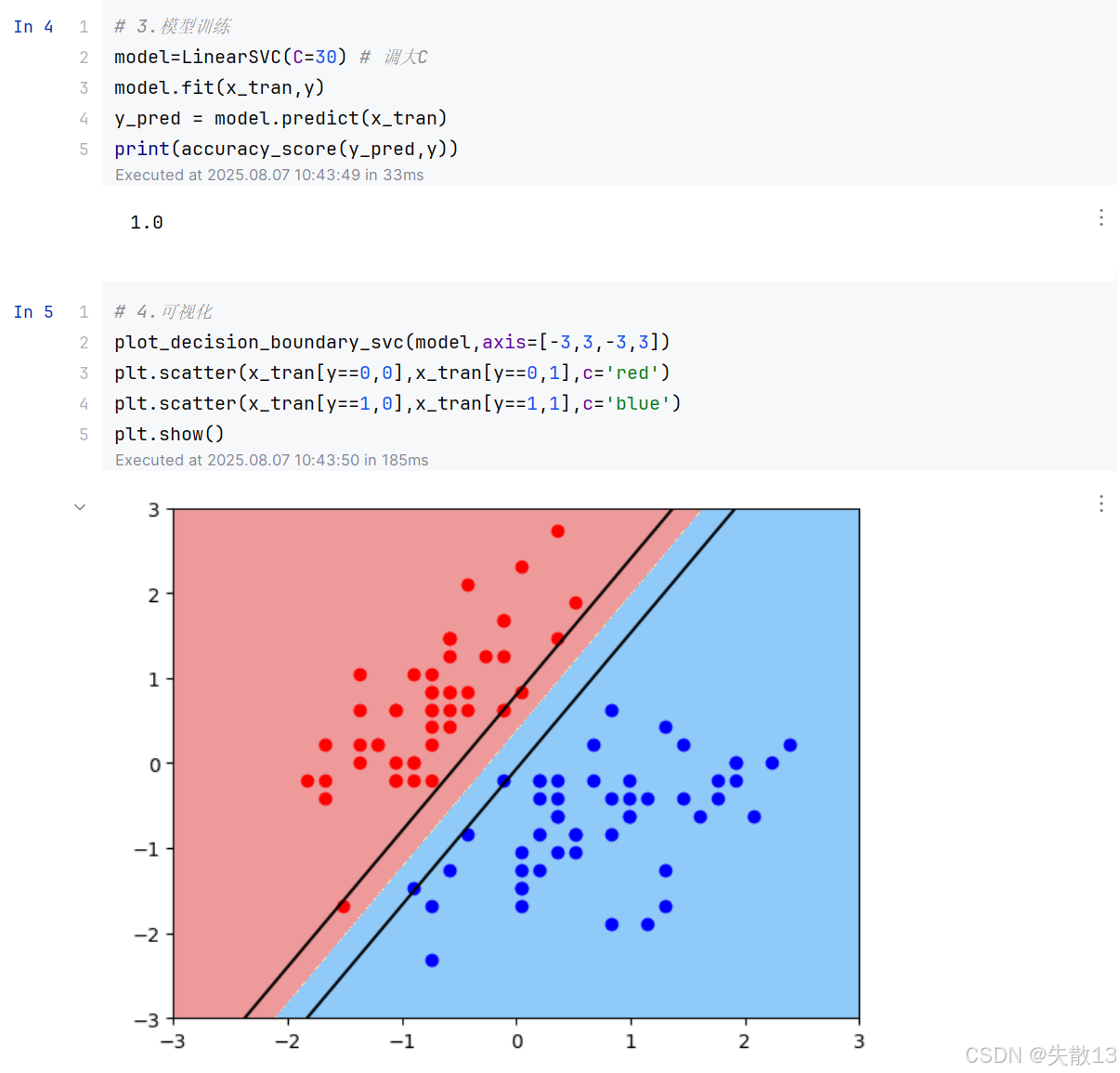
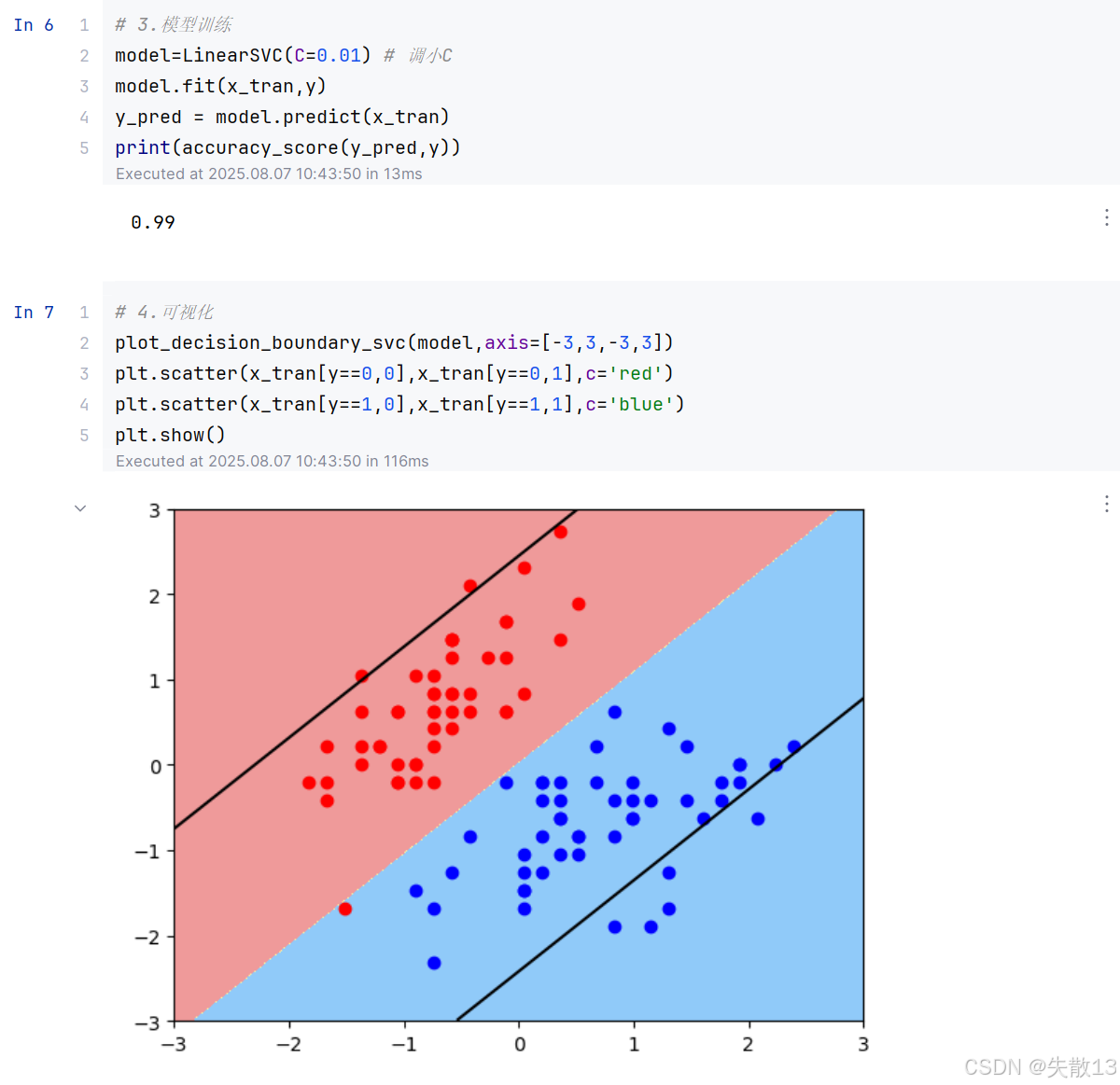
2.3 懲罰系數C對超平面的影響
-
導包、加載數據、數據預處理同上;
-
C 值越大,間隔越窄,但對間隔違例的懲罰越重;
-
C 值越小,間隔越寬,但允許的間隔違例越多;
3 SVM算法原理
3.1 支持向量機原理
-
SVM思想:找到一組參數(w,b)(w, b)(w,b),使得構建的超平面函數能夠最優地分離兩個集合;
-
樣本空間中任意點xxx到超平面(w,b)(w, b)(w,b)的距離公式:
r=∣wTx+b∣∥w∥ r = \frac{|w^T x + b|}{\|w\|} r=∥w∥∣wTx+b∣?- 其中,www是超平面的法向量,bbb是超平面的截距,xxx是樣本點,∥w∥\|w\|∥w∥是www的范數;
-
最大間隔的約束條件:
- 對于樣本點xix_ixi?和對應的標簽yiy_iyi?,有:
{wTxi+b≥+1,yi=+1wTxi+b≤?1,yi=?1 \begin{cases} w^T x_i + b \geq +1, & y_i = +1 \\ w^T x_i + b \leq -1, & y_i = -1 \end{cases} {wTxi?+b≥+1,wTxi?+b≤?1,?yi?=+1yi?=?1? - 這意味著對于正樣本(yi=+1y_i = +1yi?=+1),wTxi+bw^T x_i + bwTxi?+b至少為+1+1+1;
- 對于負樣本(yi=?1y_i = -1yi?=?1),wTxi+bw^T x_i + bwTxi?+b至多為?1-1?1;
- 對于樣本點xix_ixi?和對應的標簽yiy_iyi?,有:
-
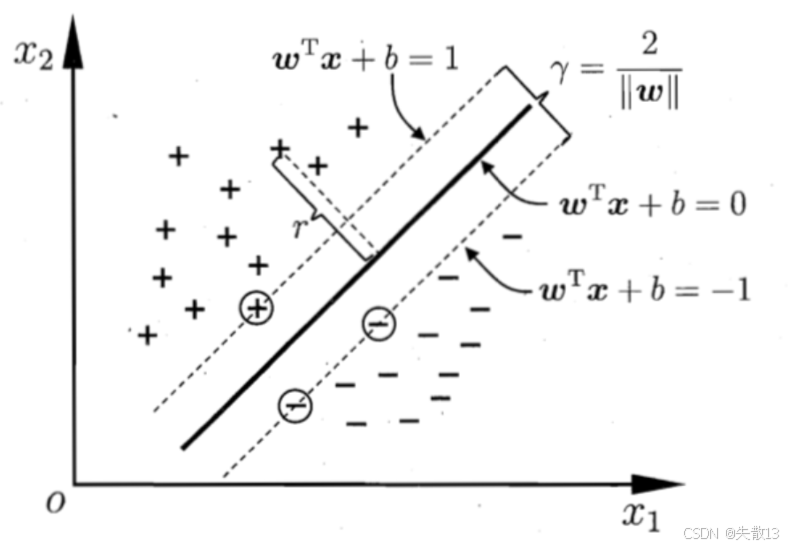
支持向量:距離超平面最近的幾個訓練樣本點,使得上述約束條件中的等號成立;
-
兩個異類支持向量到超平面的距離之和,也是最大間隔距離公式:
γ=2∥w∥ \gamma = \frac{2}{\|w\|} γ=∥w∥2?
-
目標函數:
max?w,b2∥w∥ \max_{w, b} \frac{2}{\|w\|} w,bmax?∥w∥2?- 同時滿足約束條件yi(wTxi+b)≥1y_i (w^T x_i + b) \geq 1yi?(wTxi?+b)≥1,其中i=1,2,??,mi = 1, 2, \cdots, mi=1,2,?,m;
-
目標函數的進一步優化:
min?w,b12∥w∥2 \min_{w, b} \frac{1}{2} \|w\|^2 w,bmin?21?∥w∥2- 同時滿足約束條件yi(wTxi+b)≥1y_i (w^T x_i + b) \geq 1yi?(wTxi?+b)≥1,其中i=1,2,??,mi = 1, 2, \cdots, mi=1,2,?,m;
-
添加核函數后的目標函數和約束條件:
- 目標函數:min?w,b12∥w∥2\min_{w, b} \frac{1}{2} \|w\|^2minw,b?21?∥w∥2
- 約束條件:∑i=1n(1?yi(wTΦ(xi)+b))≤0\sum_{i=1}^n (1 - y_i (w^T \Phi(x_i) + b)) \leq 0∑i=1n?(1?yi?(wTΦ(xi?)+b))≤0
- 其中,Φ(xi)\Phi(x_i)Φ(xi?)是將樣本xix_ixi?映射到高維特征空間的函數;
-
構建拉格朗日函數:L(w,b,α)=12∥w∥2?∑i=1nαi(yi(wTΦ(xi)+b)?1)L(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i (y_i (w^T \Phi(x_i) + b) - 1)L(w,b,α)=21?∥w∥2?∑i=1n?αi?(yi?(wTΦ(xi?)+b)?1)
- 其中,αi\alpha_iαi?是拉格朗日乘子;
-
對偶問題轉換:min?w,bmax?αL(w,b,α)?max?αmin?w,bL(w,b,α)\min_{w, b} \max_{\alpha} L(w, b, \alpha) \Longleftrightarrow \max_{\alpha} \min_{w, b} L(w, b, \alpha)minw,b?maxα?L(w,b,α)?maxα?minw,b?L(w,b,α)
-
對www求偏導并令其等于0:
-
首先,將拉格朗日函數展開:
L=12∥w∥2?∑i=1nαi(yiwTΦ(xi)+yib?1)L=12∥w∥2?∑i=1nαiyiwTΦ(xi)+αiyib?αi L = \frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i (y_i w^T \Phi(x_i) + y_i b - 1) \\ L = \frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i y_i w^T \Phi(x_i) + \alpha_i y_i b - \alpha_i L=21?∥w∥2?i=1∑n?αi?(yi?wTΦ(xi?)+yi?b?1)L=21?∥w∥2?i=1∑n?αi?yi?wTΦ(xi?)+αi?yi?b?αi? -
對www求偏導:
?L?w=w?∑i=1nαiyiΦ(xi)=0 \frac{\partial L}{\partial w} = w - \sum_{i=1}^n \alpha_i y_i \Phi(x_i) = 0 ?w?L?=w?i=1∑n?αi?yi?Φ(xi?)=0 -
得到:
w=∑i=1nαiyiΦ(xi) w = \sum_{i=1}^n \alpha_i y_i \Phi(x_i) w=i=1∑n?αi?yi?Φ(xi?)
-
-
對bbb求偏導并令其等于0:
- 對bbb求偏導:
?L?b=∑i=1nαiyi=0 \frac{\partial L}{\partial b} = \sum_{i=1}^n \alpha_i y_i = 0 ?b?L?=i=1∑n?αi?yi?=0 - 得到:
∑i=1nαiyi=0 \sum_{i=1}^n \alpha_i y_i = 0 i=1∑n?αi?yi?=0
- 對bbb求偏導:
-
將對www和bbb的偏導結果代入拉格朗日函數:首先,將w=∑i=1nαiyiΦ(xi)w = \sum_{i=1}^n \alpha_i y_i \Phi(x_i)w=∑i=1n?αi?yi?Φ(xi?)代入拉格朗日函數
KaTeX parse error: Can't use function '$' in math mode at position 317: … \alpha_i \\ 由于$?\sum_{i=1}^n \a…
3.2 多元支持向量機原理
-
求解當 α 是什么值時拉格朗日函數最大
α?=arg?max?α(∑i=1nαi?12∑i,j=1nαiαjyiyjΦT(xi)Φ(xj)) \alpha^* = \arg \max_{\alpha} \left( \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n \alpha_i \alpha_j y_i y_j \Phi^T(x_i) \Phi(x_j) \right) α?=argαmax?(i=1∑n?αi??21?i,j=1∑n?αi?αj?yi?yj?ΦT(xi?)Φ(xj?))-
這一步是為了找到最優的拉格朗日乘子 α\alphaα,使得拉格朗日函數最大化
-
αi\alpha_iαi? 是拉格朗日乘子,對應每個樣本的權重
-
yiy_iyi? 是樣本的標簽(+1 或 -1)
-
Φ(xi)\Phi(x_i)Φ(xi?) 是將樣本 xix_ixi? 映射到高維特征空間的函數
-
ΦT(xi)Φ(xj)\Phi^T(x_i) \Phi(x_j)ΦT(xi?)Φ(xj?) 是高維特征空間中樣本 xix_ixi? 和 xjx_jxj? 的內積
-
-
將上述公式化簡成極小值問題
min?α12∑i=1n∑j=1nαiαjyiyj(Φ(xi)?Φ(xj))?∑i=1nαi \min_{\alpha} \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j (\Phi(x_i) \cdot \Phi(x_j)) - \sum_{i=1}^n \alpha_i αmin?21?i=1∑n?j=1∑n?αi?αj?yi?yj?(Φ(xi?)?Φ(xj?))?i=1∑n?αi?-
約束條件:
s.t.?∑i=1nαiyi=0αi≥0,i=1,2,…,n \text{s.t. } \sum_{i=1}^n \alpha_i y_i = 0 \\ \alpha_i \geq 0, \quad i = 1, 2, \ldots, n s.t.?i=1∑n?αi?yi?=0αi?≥0,i=1,2,…,n -
將最大化問題轉換為最小化問題,便于求解
-
目標函數是原拉格朗日函數的對偶形式
-
約束條件確保了最優解的可行性:
- ∑i=1nαiyi=0\sum_{i=1}^n \alpha_i y_i = 0∑i=1n?αi?yi?=0 是對偶問題的約束條件
- αi≥0\alpha_i \geq 0αi?≥0 是拉格朗日乘子的非負約束
-
-
將訓練樣本帶入上面2步驟公式,求解出 αi\alpha_iαi? 值。將 αi\alpha_iαi? 值代入下面公式計算 w,bw, bw,b 的值
w?=∑i=1Nαi?yiΦ(xi)b?=yi?∑i=1Nαi?yi(Φ(xi)?Φ(xj)) w^* = \sum_{i=1}^N \alpha_i^* y_i \Phi(x_i) \\ b^* = y_i - \sum_{i=1}^N \alpha_i^* y_i (\Phi(x_i) \cdot \Phi(x_j)) w?=i=1∑N?αi??yi?Φ(xi?)b?=yi??i=1∑N?αi??yi?(Φ(xi?)?Φ(xj?))- 求解出最優的 αi?\alpha_i^*αi?? 后,代入上述公式計算超平面的參數 w?w^*w? 和 b?b^*b?
- w?w^*w? 是超平面的法向量
- b?b^*b? 是超平面的截距
-
求得分類超平面
w?Φ(x)+b?=0 w^* \Phi(x) + b^* = 0 w?Φ(x)+b?=0-
最終的分類超平面由 w?w^*w? 和 b?b^*b? 確定;
-
對于新樣本 xxx,通過判斷 w?Φ(x)+b?w^* \Phi(x) + b^*w?Φ(x)+b? 的符號來確定其類別。
-
4 SVM核函數
4.1 概述
-
核函數將原始輸入空間映射到新的特征空間,從而使原本線性不可分的樣本可能在核空間中變得可分;
- 左圖顯示了原始空間(Original space)中線性不可分的樣本(紅色和藍色點);
- 中間圖顯示了通過核函數映射到新的特征空間后,樣本變得線性可分;
- 右圖進一步展示了這種映射的效果;
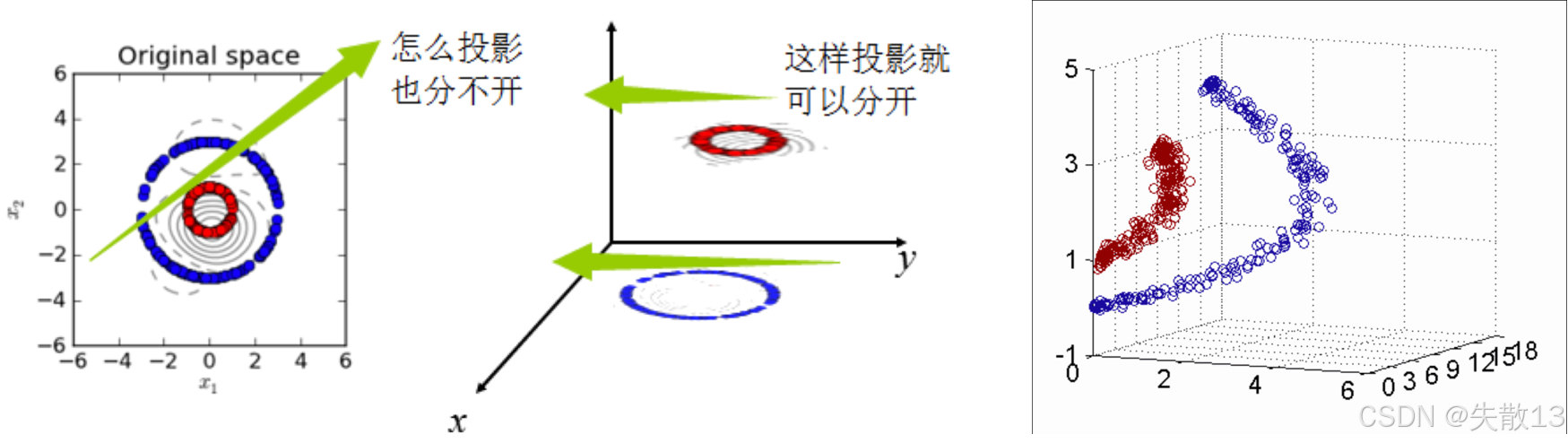
-
核函數分類:
名稱 表達式 參數 線性核 $ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = \boldsymbol{x}_i^T \boldsymbol{x}_j $ 無參數 多項式核 $ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = (\boldsymbol{x}_i^T \boldsymbol{x}_j)^d $ $ d \geq 1 $ 為多項式的次數 高斯核 $ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = \exp\left( -\frac{|\boldsymbol{x}_i - \boldsymbol{x}_j|2}{2\sigma2} \right) $ $ \sigma > 0 $ 為高斯核的帶寬(width) 拉普拉斯核 $ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = \exp\left( -\frac{|\boldsymbol{x}_i - \boldsymbol{x}_j|}{\sigma} \right) $ $ \sigma > 0 $ Sigmoid 核 $ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = \tanh(\beta \boldsymbol{x}_i^T \boldsymbol{x}_j + \theta) $ $ \tanh $ 為雙曲正切函數,$ \beta > 0 ,,, \theta < 0 $ - 高斯核(徑向基函數)是最常用的核函數之一,它可以將樣本投射到無限維空間,使得原本不可分的數據變得可分。
4.2 高斯核函數
-
高斯核函數(Radial Basis Function Kernel,RBF 核)是支持向量機(SVM)中常用的核函數之一;
K(x,y)=e?γ∥x?y∥2K(x, y) = e^{-\gamma \|x - y\|^2}K(x,y)=e?γ∥x?y∥2- $ x $ 和 $ y $ 是樣本點;$ \gamma $ 是超參數,控制高斯分布的寬度;
-
超參數 $ \gamma $ 的作用:
- $ \gamma $ 越大,高斯分布越窄,模型越容易過擬合;
- $ \gamma $ 越小,高斯分布越寬,模型越容易欠擬合;
-
圖示說明:
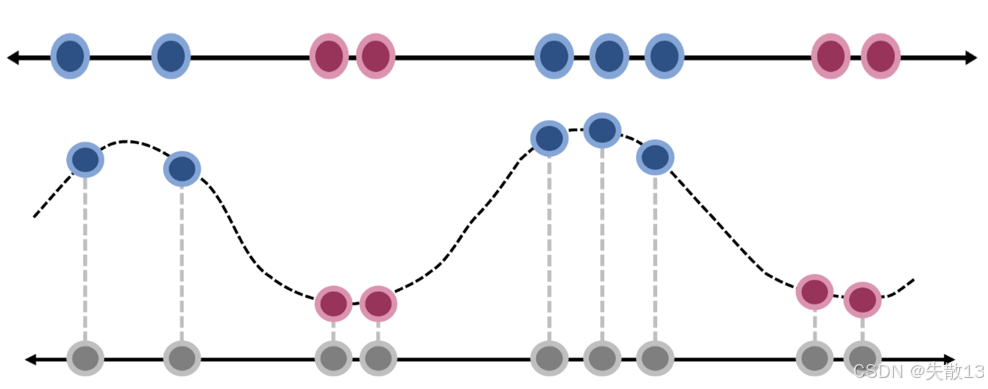
- 上方的圖顯示了原始樣本點(藍色和紅色);
- 下方的圖顯示了通過高斯核函數映射后的樣本點(藍色和紅色),可以看到樣本點在新的特征空間中變得線性可分
-
API:
- 在
scikit-learn中,可以通過以下代碼使用高斯核函數:from sklearn.svm import SVC # kernel='rbf'表示使用高斯核函數;gamma是超參數,控制高斯分布的寬度 SVC(kernel='rbf', gamma=gamma)
- 在
-
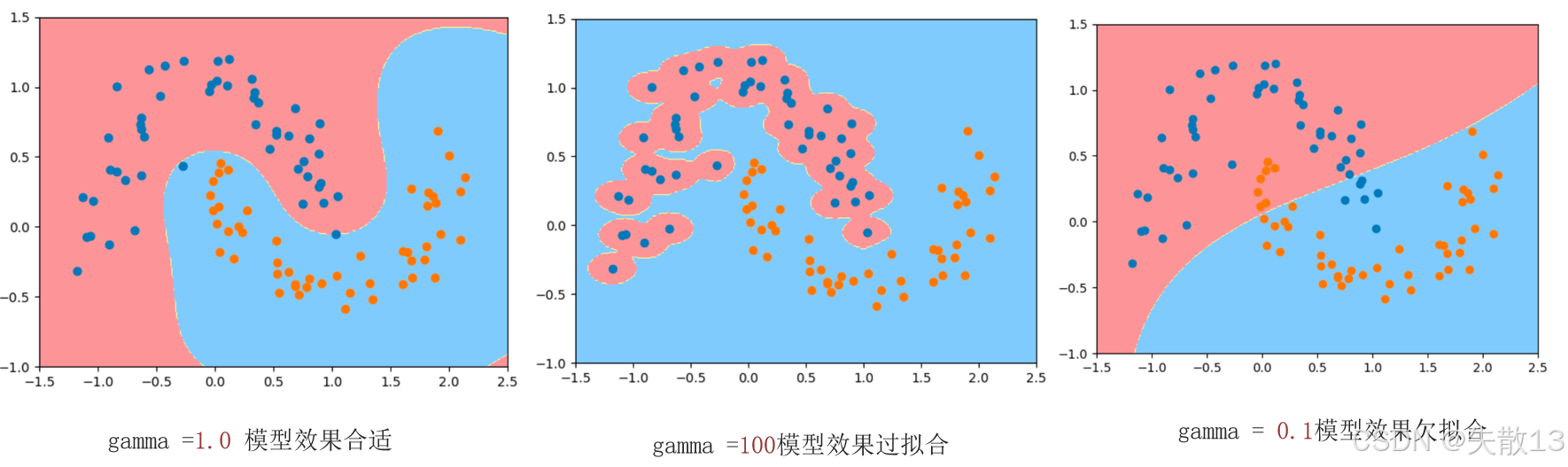
超參數 $ \gamma $ 對模型的影響:
- 左圖($ \gamma = 1.0 $):模型效果合適,分類邊界合理;
- 中圖($ \gamma = 100 $):模型效果過擬合,分類邊界過于復雜,可能在訓練集上表現很好,但在測試集上表現較差;
- 右圖($ \gamma = 0.1 $):模型效果欠擬合,分類邊界過于簡單,無法有效區分樣本;
4.3 案例
-
導包:
from sklearn.datasets import make_moons import matplotlib.pyplot as plt # 生成月牙形數據集 from sklearn.pipeline import Pipeline # 構建機器學習工作流的管道 from sklearn.preprocessing import StandardScaler from sklearn.svm import SVC # 支持向量機分類器 from plot_util import plot_decision_boundary # 自定義的決策邊界繪制工具 -
準備數據:
# 準備數據 # 生成帶有噪聲的月牙形數據集,noise=0.15控制噪聲大小 # 月牙形數據是典型的非線性可分數據,適合展示核函數的效果 x,y=make_moons(noise=0.15) # 可視化原始數據分布 # 繪制標簽為0的樣本點 plt.scatter(x[y==0, 0], x[y==0, 1]) # 繪制標簽為1的樣本點 plt.scatter(x[y==1, 0], x[y==1, 1]) # 顯示圖形,可觀察到數據呈月牙狀分布,線性不可分 plt.show()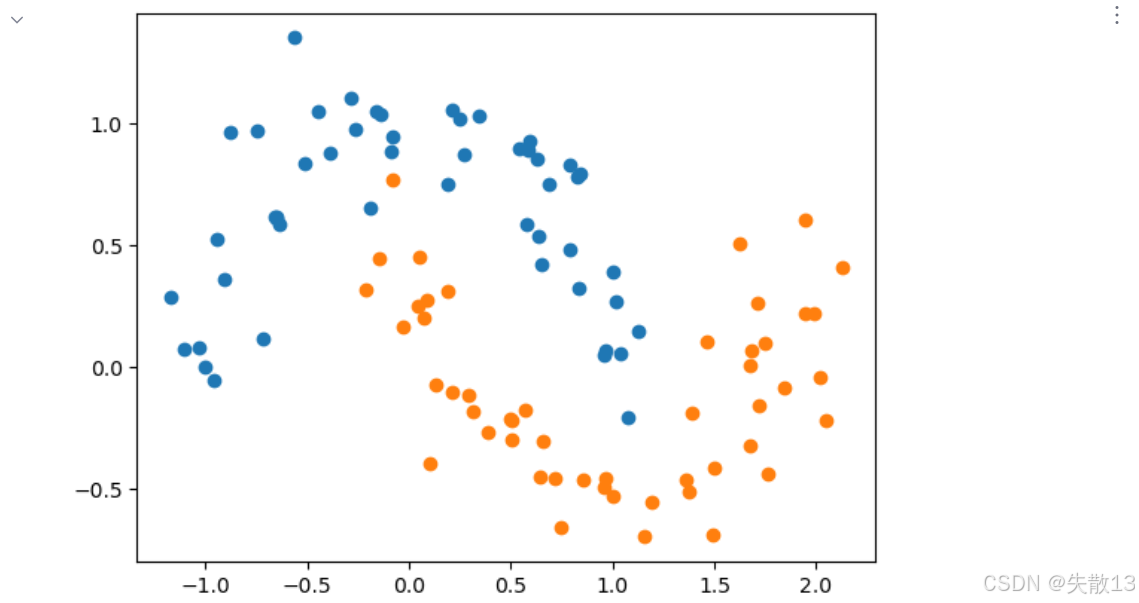
-
構建函數:
# 構建函數:創建使用RBF核的SVM模型管道 def RBFsvm(gamma=0.1):# Pipeline用于將數據預處理和模型訓練步驟串聯起來return Pipeline([# 第一步:數據標準化,將特征轉換為均值為0、標準差為1的分布('std_scalar', StandardScaler()),# 第二步:使用SVM分類器,指定核函數為RBF(徑向基函數)# gamma是RBF核的超參數,控制高斯函數的寬度('svc', SVC(kernel='rbf', gamma=gamma))]) -
實驗1:
# 實驗1:gamma=0.5時的模型效果 # 創建gamma=0.5的RBF SVM模型 svc1 = RBFsvm(0.5) # 單獨獲取管道中的標準化器,對數據進行標準化處理 x_std = svc1['std_scalar'].fit_transform(x) # 使用標準化后的數據訓練模型 svc1.fit(x_std, y) # 繪制決策邊界,設置坐標軸范圍 plot_decision_boundary(svc1, axis=[-3, 3, -3, 3]) # 在決策邊界圖上繪制標準化后的樣本點 plt.scatter(x_std[y==0, 0], x_std[y==0, 1]) plt.scatter(x_std[y==1, 0], x_std[y==1, 1]) # 顯示圖形,可觀察到較合理的分類邊界 plt.show()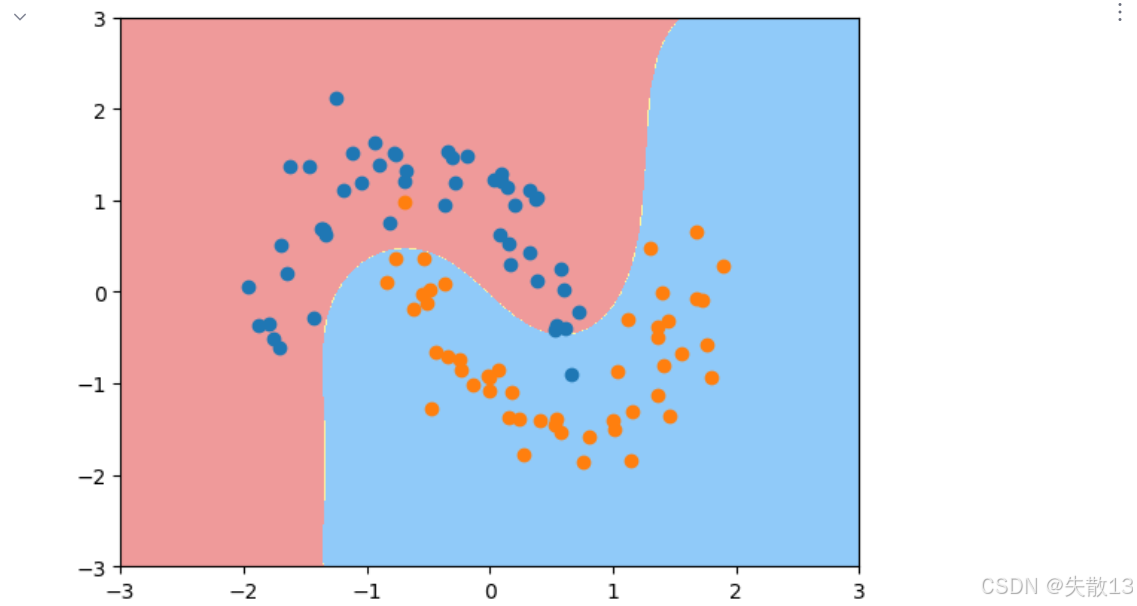
-
實驗2:
# 實驗2:gamma=1.0時的模型效果 # 創建gamma=1.0的RBF SVM模型 svc1 = RBFsvm(1.0) # 使用原始數據訓練模型(管道內部會自動進行標準化) svc1.fit(x, y) # 繪制決策邊界,設置適合原始數據的坐標軸范圍 plot_decision_boundary(svc1, axis=[-1.5, 2.5, -1, 1.5]) # 繪制原始樣本點 plt.scatter(x[y==0, 0], x[y==0, 1]) plt.scatter(x[y==1, 0], x[y==1, 1]) # 顯示圖形,邊界比gamma=0.5時更復雜一些 plt.show()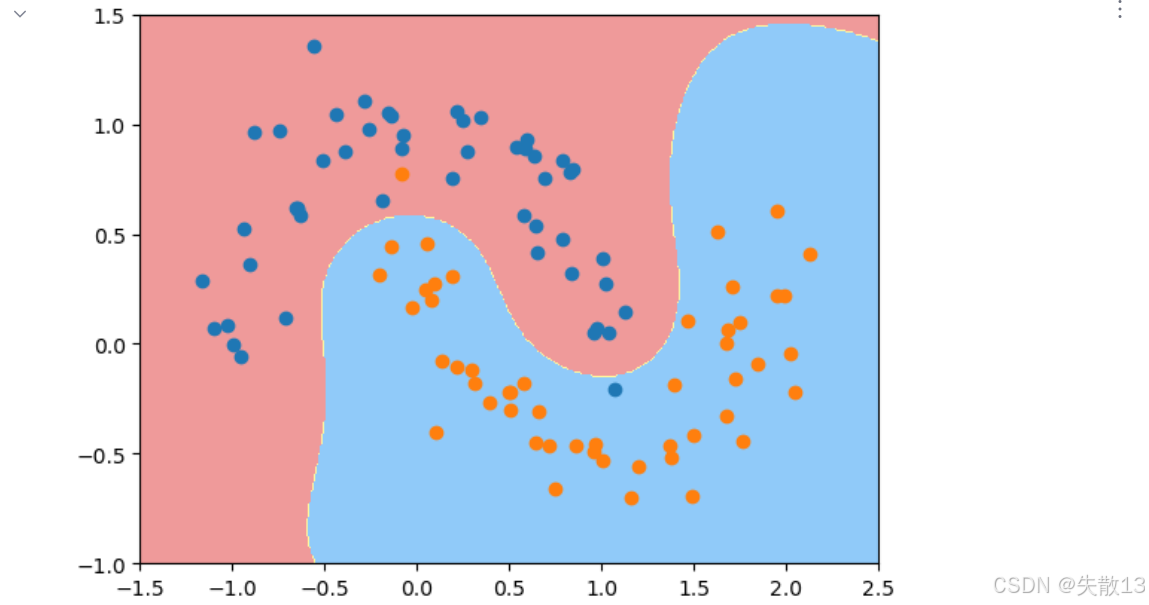
-
實驗3:
# 實驗3:gamma=100時的模型效果 # 創建gamma=100的RBF SVM模型 svc2 = RBFsvm(100) svc2.fit(x, y) plot_decision_boundary(svc2, axis=[-1.5, 2.5, -1, 1.5]) plt.scatter(x[y==0, 0], x[y==0, 1]) plt.scatter(x[y==1, 0], x[y==1, 1]) # 顯示圖形,可觀察到過擬合現象: # 決策邊界非常復雜,過度擬合了訓練數據中的噪聲 plt.show()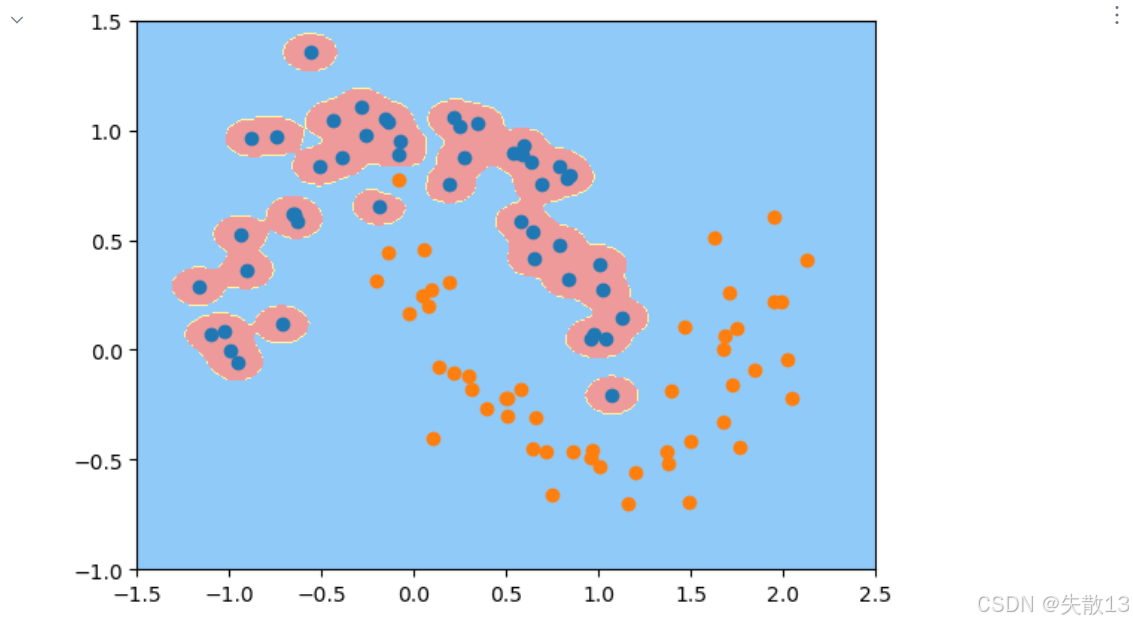
-
實驗4:
# 實驗4:gamma=0.1時的模型效果 # 創建gamma=0.1的RBF SVM模型 svc3 = RBFsvm(0.1) svc3.fit(x, y) plot_decision_boundary(svc3, axis=[-1.5, 2.5, -1, 1.5]) plt.scatter(x[y==0, 0], x[y==0, 1]) plt.scatter(x[y==1, 0], x[y==1, 1]) # 顯示圖形,可觀察到欠擬合現象: # 決策邊界過于簡單,無法很好地區分兩類數據 plt.show()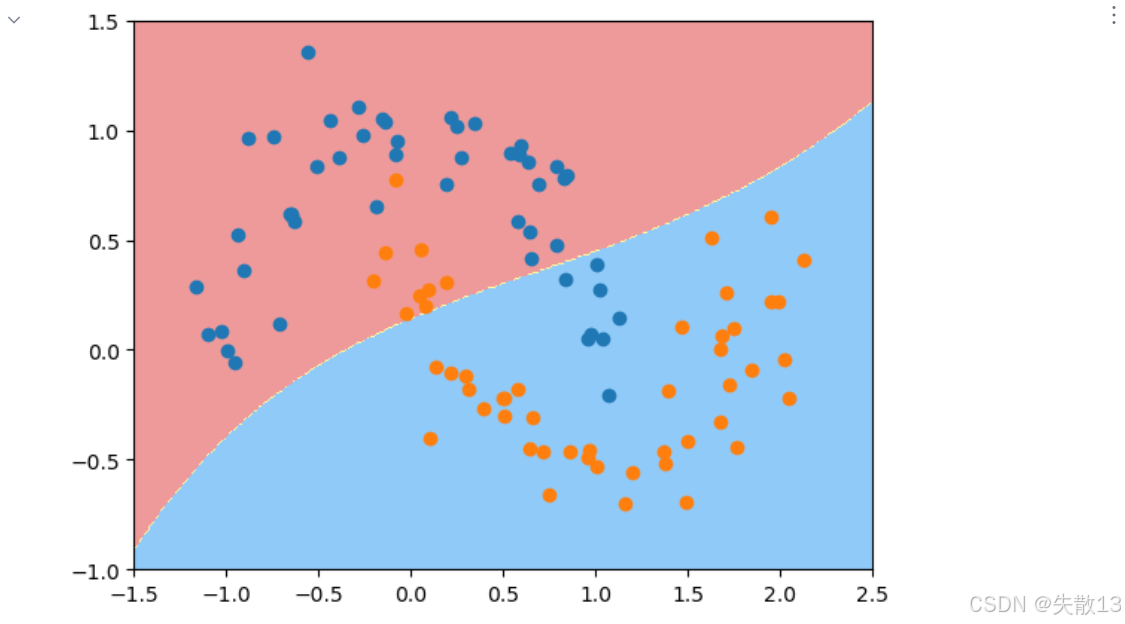
4.4 超參數 gamma 的意義和作用
-
高斯核函數(RBF)表達式:
K(x,y)=e?γ∥x?y∥2 K(x, y) = e^{-\gamma \|x - y\|^2} K(x,y)=e?γ∥x?y∥2 -
對比高斯函數:
g(x)=1σ2πe?12(x?μσ)2 g(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2} g(x)=σ2π?1?e?21?(σx?μ?)2 -
超參數
gamma的意義:- 高斯核函數中的
gamma(γ\gammaγ)等價于高斯函數中的 12σ2\frac{1}{2\sigma^2}2σ21?; gamma控制高斯分布的寬度;
- 高斯核函數中的
-
標準差(σ\sigmaσ)對數據分布的影響
-
標準差越大:數據越分散,圖像越寬;
-
標準差越小:數據越集中,圖像越窄;
-
-
超參數
gamma對模型的影響-
gamma越大:高斯分布越窄,數據變化越劇烈,模型容易過擬合; -
gamma越小:高斯分布越寬,數據變化越平緩,模型容易欠擬合;
-
-
看下圖中曲線:
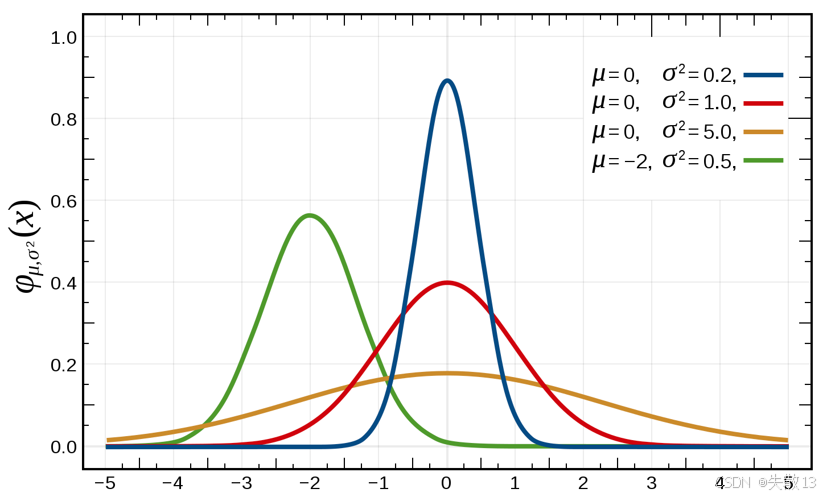
- 藍色曲線:μ=0,σ2=0.2\mu = 0, \sigma^2 = 0.2μ=0,σ2=0.2(數據集中,圖像窄)
- 紅色曲線:μ=0,σ2=1.0\mu = 0, \sigma^2 = 1.0μ=0,σ2=1.0(數據較集中,圖像較窄)
- 橙色曲線:μ=0,σ2=5.0\mu = 0, \sigma^2 = 5.0μ=0,σ2=5.0(數據分散,圖像寬)
- 綠色曲線:μ=?2,σ2=0.5\mu = -2, \sigma^2 = 0.5μ=?2,σ2=0.5(數據集中,圖像窄)








)

)

詳細對比)
Java 工廠模式)

進程狀態)



