一、主成分分析

????????主成分分析是多元統計分析的一種常用的降維方法，它以盡量少的信息損失，最大程度將變量個數減少，且彼此間互不相關。提取出來的新變量成為主成分，主成分是原始變量的線性組合。

1.1?KMO檢驗和Bartlett球形檢驗??

????????在進行主成分分析和因子分析之前，需要進行KMO和Bartlett球形檢驗。當KMO檢驗系數>0.5，Bartlett球形檢驗的P值<0.05時，數據才比較適合進行主成分分析或因子分析。這兩個檢驗是用于檢查變量的信息重疊度，當檢驗通過時說明多變量相關性較大，有信息重疊，才會適合做主成分分析降低維度。

????????KMO檢驗的實現來自[R] KMO sampling adequacy and SPSS -- partial solution

????????Bartlett球形檢驗使用psych包內的cortest.bartlett()函數

kmo()用法：kmo(data)

??????????? kmo()函數只需要輸入標準化數據即可，返回的overall為檢驗系數

cortest.bartlett()用法：cortest.bartlett(R,n=NULL,diag=TRUE)

????????其中參數R為相關陣

????????n為樣本量，即觀測數量

????????diag=T時將對角線矩陣換成1，使其成為相關陣

例1：

????????試對下列數據進行主成分分析

序號	省份	工資性收入	家庭性收入	財產性收入	轉移性收入
1	北京	4524.25	1778.33	588.04	455.64
2	天津	2720.85	2626.46	152.88	79.64
3	河北	1293.50	1988.58	93.74	105.81
4	山西	1177.94	1563.52	62.70	86.49
5	內蒙古	504.46	2223.26	73.05	188.10
6	遼寧	1212.20	2163.49	113.24	201.28

注：以上僅為部分表格

> data2=read.csv('Table_0.csv',encoding='UTF-8')
> rownames(data2)=data2[,1]
> data2=data2[,-1]
> st.data2=scale(data2)		#標準化數據
> library(psych)
> source("kmo.R")
> kmo(st.data2)$overall		#kmo檢驗
[1] 0.7404854
> cortest.bartlett(cor(st.data2),nrow(st.data2))	#巴特利特球形檢驗
$chisq
[1] 68.86313$p.value
[1] 6.992923e-13$df
[1] 6

????????由檢驗結果可見，kmo檢驗系數大于0.5，Bartlett球形檢驗的P值極小

????????說明這個數據的變量信息重疊較多，適合進行主成分分析和因子分析

1.2 主成分分析函數介紹

????????R語言中進行主成分分析的函數有自帶的princomp()函數，也有psych包內的principal()函數。兩個函數雖然都是用于主成分分析，但是兩個函數會有所區別。本文會同時介紹兩個函數

princomp()用法：princomp(x,cor=FALSE,scores=TRUE,…)

????????princomp()也有formula參數用法，但是我們較少使用，所以只介紹默認用法。

????????x是數據矩陣或數據框，通常要先進行標準化

????????cor參數是一個邏輯值，當cor=T時使用相關陣進行主成分分析，默認cor=F，此時用協差陣進行主成分分析

????????scores參數也是一個邏輯值，表示是否計算主成分得分

principal()用法：principal(r,nfactors=1,rotate=”varimax”,n.obs=NA,scores=TRUE,…)

????????r可以是數據矩陣或數據，也可以是相關陣

????????rotate參數指定主成分旋轉方法，默認為最大方差法，其他的方法還有

??????????? ”none”不進行旋轉

??????????? “quartimax”、”promax”、”oblimin”、”simplimax”、”cluster”

????????簡單的主成分分析的旋轉方法除了”none”和”varimax”使用較多外，其他都較少使用

????????scores參數的用法和princomp()函數里的scores參數相同，都是表示是否計算主成分得分

????????n.obs是原始數據的樣本量，也就是觀測的個數。當r是相關陣時需要指定n.obs，但如果r是原始數據則不用指定

????????principal()與 princomp() 不同，它只返回最佳主成分個數的子集。特征向量按特征值的開方重新縮放，以產生在因子分析中更典型的分量載荷。principal()需要提前確定最佳主成分個數，而princomp()是直接把所有主成分提取出來，再通過方差累計貢獻率確定主成分個數。所以在使用principal()進行主成分分析之前，我們需要通過一些方法確定主成分的個數

1.3 確定主成分個數(principal)

????????提前確定主成分個數的方法，無外乎畫碎石圖，我們可以用同樣來自于psych包內的fa.parallel()函數來確定。fa.parallel()不僅可以用于確定主成分個數，也可以用于確定因子分析時因子的個數，這個函數在下文的因子分析也有用到

fa.parallel()用：fa.parallel(x,n.obs=NULL,fm=”minres”,fa=”both”,…)

????????x可以是數據矩陣或數據框，也可以是相關陣

????????n.obs的用法和principal()內的n.obs用法相同，也就是當x取相關陣時需要指定的觀測個數

????????fm指定提取因子的方法，默認為”minres”極小殘差法。此外還可以選擇

??????????? “ml”——極大似然法；“pa”——主軸迭代法

??????????? “wls”——加權最小二乘法；”gls”——廣義最小二乘法

????????提取因子的方法用極大似然法計算會比較快，但是在某些情況可能不收斂，選用主軸迭代法會比較穩妥。這個主要在因子分析時會用到。

????????fa指定提取主成分還是因子，fa=”pc”時只提取主成分，fa=”fa”時只提取因子，fa=”both”時主成分和因子都提取

????????碎石圖評估主成分個數的具體方法時查看高度為1的橫線或兩條紅色虛線上方的散點個數。橫線是特征值為1的高度，紅色虛線是隨機數據矩陣的平均特征值。在主成分或因子個數增加的時候，如果真實數據特征值低于隨機數據的平均特征值，這時候說明之后的因子或主成分沒有保留的價值。

續上例：

> fa.parallel(st.data2,fm='pa',fa='pc')		#只確定主成分個數
Parallel analysis suggests that the number of factors =  NA  and the number of components =  1

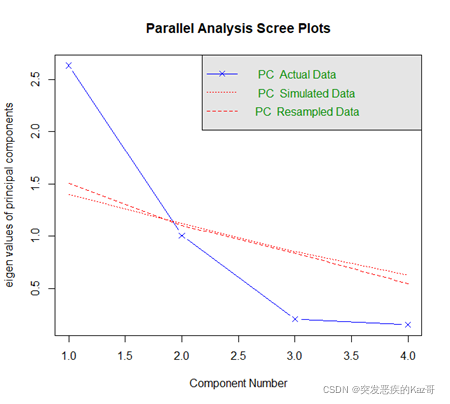
????????在隨機數據平均特征值以上的只有第一特征值，函數推薦保留一個主成分。但是第二個特征值離隨機數據的平均特征值也不遠，而且到第三特征值的下降程度還比較大，只保留一個主成分的建議還比較存疑。到底需不需要只保留一個主成分可以在主成分分析完后查看方差累計貢獻率確定。

1.4 進行主成分分析

????????如果用princomp()進行主成分分析可以跳過前一步，這個函數的主成分個數確定在主成分分析之后。而用principal()進行主成分分析則需要提前確定主成分個數。

????????對于princomp()的主成分分析結果，需要用summary()函數獲取各個主成分的方差、方差累計貢獻率和載荷陣，查看可以通過princomp對象的loadings組件獲取，也可以在summary()函數內加入loadings參數獲取。

? ? ? ?而principal()的主成分分析結果，查看儲存結果的變量可以獲取大部分信息，只查看載荷陣和方差累計貢獻率也可以通過principal對象的loadings組件獲取。

續上例：

> prc1=princomp(st.data2,cor=T)		#用princomp進行的主成分分析
> prc2=principal(st.data2,nfactor=1)	#用principal進行的主成分分析
> summary(prc1,loadings=T)		#查看princomp的主成分分析結果
Importance of components:Comp.1    Comp.2     Comp.3     Comp.4
Standard deviation     1.6221839 1.0039536 0.45568337 0.39108742
Proportion of Variance 0.6578701 0.2519807 0.05191183 0.03823734
Cumulative Proportion  0.6578701 0.9098508 0.96176266 1.00000000Loadings:Comp.1 Comp.2 Comp.3 Comp.4
工資性收入  0.582         0.314  0.749
家庭性收入         0.989  0.117       
財產性收入  0.568  0.124 -0.806 -0.111
轉移性收入  0.579         0.488 -0.651#Cumulative Proportion是方差累計貢獻率
#可見在第二個主成分以及到達較高水平> prc2$loadings				#查看principal對象的載荷陣和累計方差貢獻率Loadings:PC1   
工資性收入  0.944
家庭性收入 -0.102
財產性收入  0.921
轉移性收入  0.939PC1
SS loadings    2.631
Proportion Var 0.658		#單個主成分的累計方差貢獻率只有65.8%，不高
#這說明自提取一個主成分有點不太合適
#再用principal進行兩個主成分的主成分分析
> prc2=principal(st.data2,nfactor=2)
> prc2$loadingsLoadings:RC1    RC2   
工資性收入  0.945       
家庭性收入         0.998
財產性收入  0.928       
轉移性收入  0.931 -0.136RC1   RC2
SS loadings    2.622 1.018
Proportion Var 0.655 0.254
Cumulative Var 0.655 0.910		#兩個主成分的累計貢獻率達到91%的較高水平

1.5 確定主成分個數(princomp)

????????princomp()的主成分分析會提取所有主成分，確定其主成分個數我們要從累計方差貢獻率或碎石圖確定。

????????對princomp對象使用summary()函數獲取累計方差貢獻率，Cumulative Proportion就是累計方差貢獻率，通常取主成分個數使累計方差貢獻率達到一個較高的百分數(如85%以上)。

????????確定princomp()的主成分個數也可以通過畫碎石圖確定，畫princomp對象碎石圖的函數為screeplot()

screeplot()用法:screeplot(x,npcs=min(10,length(x$sdev)),type=c(“barplot”,”lines”),…)

????????x是princomp()的主成分分析結果

????????npcs是需要繪制的主成分個數，默認取10和x全部主成分個數之間的最小值

????????type指定繪圖的類型，type=”barplot”時繪制直方圖，type=”line”時繪制折線圖

????????這個函數繪制的碎石圖沒有隨機數據的平均特征值作為參考。我們可以通過下降程度或繪制特征值為1的水平線來判斷。再特征值1的水平線上的散點個數，或者下降到一個較低水平的主成分之前的個數。

續上例：

#prc1是princomp對象
#上文以通過summary()函數已經到兩個主成分時到達了較高的累計貢獻率
> screeplot(prc1,type='line')
> abline(1,0,col='blue')	#添加特征值1水平線

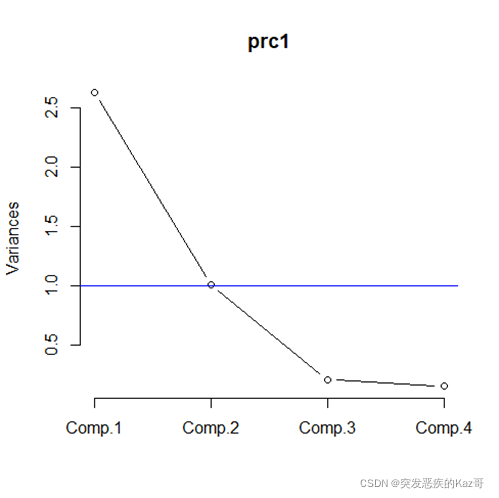
?????????由圖看，選取兩個主成分是比較合適的

1.6 獲取主成分得分以及進行綜合評價

?1.6.1 獲取主成分得分

????????進行主成分分析的主要目的是對數據進行降維，確定好主成分個數后，可以通過scores組件獲取原數據在各個主成分上的得分，并用主成分的得分代替原變量進行其他分析

????????主成分的得分就是各個樣品主成分的值，主成分是標準化后的原始變量的線性組合，將每個樣品標準化原始變量的值代入主成分的表達式里也可以獲得主成分得分。

????????princomp對象會返回所有主成分的得分，我們只提取需要的前幾個主成分得分即可

????????principal對象只返回m個主成分的得分，m記為我們確定的主成分個數

續上例：

> head(prc1$scores[,1:2])Comp.1     Comp.2
北京    4.58987415  0.3734869
天津    0.28101544  1.7953881
河北   -0.44296144  0.3489825
山西   -0.65163291 -0.5607793
內蒙古 -0.60834766  0.7533096
遼寧   -0.05120586  0.6893062
> head(prc2$scores)RC1        RC2
北京    2.80352044  0.1472879
天津    0.30740034  1.7405353
河北   -0.24107468  0.3619058
山西   -0.43690909 -0.5169196
內蒙古 -0.31009603  0.7647188
遼寧    0.02183515  0.6757876

1.6.2 進行綜合評價

????????另外，我們可以利用主成分分析的得分對各個樣品進行綜合評價。主成分分析能從選定的指標體系中歸納出大部分信息，根據主成分提供的信息進行綜合評價是一種可行的選擇。

每個樣品的綜合評價得分是主成分得分的加權和，每個主成分的權重等于所屬特征值除以m個特征根的和，這里m指所選主成分個數。

對princomp()和principal()兩個函數主成分分析結果，進行綜合評價的函數實現為如下，該函數同時對每個樣品的綜合評價得分進行了排序

evaluation=function(prin,data=NULL,nfactor=NULL){#當prin是princomp返回的主成分分析結果時,data和nfactor不可缺#data是標準化數據，用于獲取特征值#nfactor是選擇的主成分個數which=class(prin)[length(class(prin))]if(which=='princomp') {if(is.null(data)|is.null(nfactor)) {print('需輸入原始數據和主成分個數');stop()}else{values=eigen(cor(data))$values[1:nfactor]w=values/sum(values);scores=prin$scores[,1:nfactor]}}#當prin是psych包內的principal函數返回的主成分分析結果時#特征值和主成分個數可以通過調用組件獲取else if(which=='principal') {scores=prin$scores;nfactor=ncol(scores)values=prin$values[1:nfactor];w=values/sum(values)}eva.scores=scores%*%wfinal.eva=as.numeric(eva.scores)names(final.eva)=rownames(eva.scores)sort(final.eva,T)
}

續上例：

#對各個樣品進行綜合評價
> source(“evaluation.R”)
> evaluation(prc1,st.data2,2)上海       北京       浙江       江蘇       福建       天津       廣東     黑龍江 4.0900564  3.4221571  2.1177097  0.8304684  0.7029739  0.7004168  0.6631721  0.3083484 吉林       遼寧       山東       河北     內蒙古       海南       西藏       湖南 0.1738328  0.1538769  0.0554438 -0.2236347 -0.2312404 -0.3985562 -0.4122491 -0.4853280 寧夏       重慶       四川       湖北       江西       山西       河南       新疆 
-0.5463658 -0.6151700 -0.6180057 -0.6203514 -0.6264414 -0.6264713 -0.7128601 -0.7134170 青海       安徽       云南       陜西       廣西       甘肅       貴州 
-0.7150107 -0.7755070 -0.8726009 -0.9127242 -0.9854052 -1.0570477 -1.0700698 
> evaluation(prc2)上海        北京        浙江        天津        江蘇        福建      黑龍江 2.08066022  2.06788405  1.59581510  0.70430316  0.60117700  0.58466717  0.37857458 廣東        吉林        遼寧        山東      內蒙古        海南        河北 0.36999921  0.29433837  0.20294550  0.18165695 -0.01242897 -0.06809526 -0.07408087 湖北        新疆        湖南        江西        河南        四川        寧夏 
-0.29972298 -0.32625842 -0.33136881 -0.38913165 -0.39577186 -0.42128328 -0.42511876 西藏        山西        重慶        安徽        青海        云南        廣西 
-0.44160741 -0.45906777 -0.46972445 -0.57218090 -0.58965530 -0.61776827 -0.69206531 陜西        甘肅        貴州 
-0.78365886 -0.82534403 -0.86768814

二、因子分析

????????因子分析和主成分分析有點相似，但兩種分析的出發點和結果都不同。主成分分析是試圖尋找原變量的線性組合，使得這個組合的方差最大，使其攜帶的信息最多。因子分析是尋找對原變量都有影響的潛在變量，這種潛在變量往往難以量化，這個潛在變量稱為公共因子，公共因子可以賦予一定的現實意義。

????????R中進行因子分析的函數是psych包內的fa()函數。psych包內的部分函數在上文的主成分分析中也有介紹。這個函數進行的為R型因子分析，Q型因子分析此處不做介紹。

2.1 KMO檢驗和Bartlett球形檢驗

????????在進行因子分析和主成分分析之前都需要進行KMO和Bartlett球形檢驗。這兩個分析的介紹在上文的主成分分析已經給出，此處不贅述

例2：

對上一例題的數據進行因子分析

由上文進行主成分分析之前的kmo和Bartlett球形檢驗結果，可知該數據適合做因子分析

2.2 確定因子個數

????????上文介紹了psych包內的fa.parallel()函數，這個函數通過畫原始數據和隨機數據的碎石圖來確定主成分或因子個數。我們令fa.parallel()的fa參數為”fa”，這樣繪制的是因子的碎石圖，用于確定因子個數

續上例：

> fa.parallel(st.data2,fm='pa',fa='fa')
Parallel analysis suggests that the number of factors =  1  and the number of components =  NA
There were 32 warnings (use warnings() to see them)

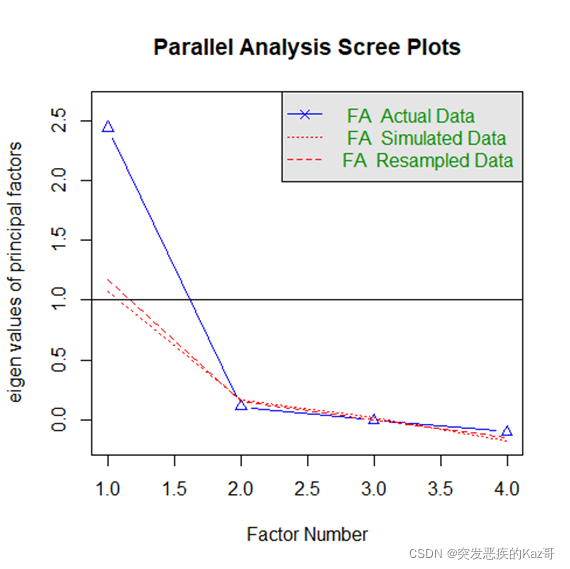
?????????函數建議的因子個數為1個，從碎石圖看也是1個比較合適。暫且先以1個因子進行因子分析

2.3 進行因子分析

????????進行因子分析需要用fa()函數

fa()用法：fa(r,nfactors=1,n.bos=1,rotate=”oblimin”,fm=”minres”,…)

????????這些參數與主成分分析中的principal()函數的參數用法相同

????????r為標準化數據或相關陣，nfactors指定因子個數

????????n.bos指定樣本量，當r是相關陣時需要指定

????????rotate是因子旋轉方法，默認為”oblimin”斜交轉軸法，我們常用的是”varimax”最大方差法或”none”不旋轉

????????fm指定提取公共因子的方法，默認為”minres”極小殘差法。此外還可以選擇

??????????? “ml”——極大似然法；“pa”——主軸迭代法

??????????? “wls”——加權最小二乘法；”gls”——廣義最小二乘法

????????fa()函數返回的分析結果有以下常用組件

????????????????communality——公共因子方差

????????????????values——特征根

????????????????loadings——載荷陣及因子方差貢獻率

????????????????scores——因子得分

????????????????rot.mat——因子旋轉矩陣

????????直接查看存儲了因子分析結果的變量可以獲取載荷陣、共同度等信息

續上例：

> FA1=fa(st.data2,nfactors=1,rotate='varimax',fm='pa')
> FA1$loadingsLoadings:PA1   	#根據載荷陣可以知道因子與哪些原始變量關系密切
工資性收入  0.928
家庭性收入       	#家庭性收入的載荷太小不顯示
財產性收入  0.866	#這可能導致因子解釋不夠充分
轉移性收入  0.910PA1
SS loadings    2.444
Proportion Var 0.611	#一個因子只解釋了原始數據61.1%的信息
#嘗試提取兩個公共因子
> FA2=fa(st.data2,nfactors=2,rotate='varimax',fm='pa')
> FA2$loadingsLoadings:PA1    PA2   
工資性收入  0.910       
家庭性收入         0.396		#第二個公共因子對家庭性收入的載荷也不高
財產性收入  0.897       
轉移性收入  0.905 -0.291PA1   PA2
SS loadings    2.451 0.253
Proportion Var 0.613 0.063
Cumulative Var 0.613 0.676		#累計方差貢獻率依然不高
#兩個因子和一個因子對原始數據的解釋程度相差不大
#這樣只取一個因子會比較好

2.4 構建新的指標體系以及獲取得分

?????????通過載荷陣查看公共因子與原始變量的載荷，在一個公共因子上載荷較大的原始變量，它與這個公共因子的關系會比較密切。我們可以根據載荷高的變量對公共因子賦予一定的現實意義，以此構建新的指標體系

????????例如以高中各個學科成績為原始變量的指標體系，提取兩個公共因子，第一公共因子對數學、物理、化學的載荷較大，第二公共因子對語文、英語、歷史、政治的載荷較大，那么我們可以將第一公共因子定義為理科能力，第二公共因子定義為文科能力，并將原始的指標體系簡化為由理科能力和文科能力兩個新指標組成

?????????由于公共因子也是標準化原始數據的線性組合，根據載荷可以計算出每個樣品的因子得分。對fa()函數返回的因子分析結果，我們也可以通過查看scores組件獲得因子得分

續上例：

#以FA1為例 
#因為只有一個因子，原始變量都是收入相關
#可以將公共因子定義為收入水平
> head(FA1$scores)			#展示前6個樣品的因子得分PA1
北京    2.520412846
天津    0.281677988
河北   -0.242683221
山西   -0.383635155
內蒙古 -0.347368818
遼寧   -0.009437811

三、相應分析

????????相應分析又稱為對應分析，其是對兩個定性變量的多水平進行相應研究，查看它們之前的內在聯系。相應分析也是聯系R型因子分析和Q型因子分析的橋梁

????????相應分析基于計數列聯表數據，在R中進行簡單相應分析，可以用MASS包中的corresp()函數，也可以用ca包中的ca()函數

????????以列聯表出發進行簡單相應分析的步驟很簡單，只需三步。，一是對列聯表進行獨立性檢驗，二是用相應分析的函數進行相應分析，三是用畫圖函數畫出相應分析圖，將各個水平在相應分析圖中表示出來，離得近的就是不同因素的比較類似的水平

3.1 構建列聯表

????????有時候我們拿到的數據是每個觀測的未分組數據，此時我們需要用table()函數對每個水平進行計數，構建列聯表。

table()用法：table(x,y,…)

????????x與y就是我們需要進行計數的變量，這兩個變量通常需要先轉化成因子

例3：

????????試對1991 U.S.GSS數據中的race（種族）和Happy（幸福）進行相應分析，并說明它們兩者的對應關系

sex	race	region	happy	life	sibs
2	1	1	1	1	1
2	1	1	2	1	2
1	1	1	1	0	2
2	1	1	9	2	2
2	2	1	2	1	4

注：以上僅為部份表格

> data3=read.csv('1991 U.S. General Social Survey.csv')
> data3=data3[,c(2,4)]			#提取種族和幸福兩個變量
> data3[,1]=as.factor(data3[,1])
> data3[,2]=as.factor(data3[,2])
> head(data3)race happy
1    1     1
2    1     2
3    1     1
4    1     9
5    2     2
6    2     2
> attach(data3)
> table3=table(race,happy)	#做列聯表
> table3happy
race   1   2   3   91 409 730 117   82  46 116  39   33  12  26   9   2

3.2 獨立性檢驗

????????進行相應分析前需要對行列因子進行獨立性檢驗。如果行列獨立，說明這兩個因素相互沒有影響，也就沒有做相應分析的必要了。在R中，進行獨立性檢驗的函數主要是chisq.test()，用的是皮爾遜卡方檢驗。此外還可以用Deducer包內的likelihood.test進行似然比獨立性檢驗

chisq.test()用法：chisq.test(x,y=NULL,…)

????????x可以是矩陣、數據框、表，也可以是因子(factor)。當x是矩陣或數據框或表時，內容應該是計數數據，即x本質上應該是列聯表，此時是對列聯表的行列因子進行獨立性卡方檢驗

????????y是因子(factor)，當x是列聯表時可以忽略這個參數。當x和y都是因子時，會對x和y的獨立性進行檢驗。

likelihood.test()用法：likelihood.test(x,y=NULL,…)

????????這個函數的用法與chisq.test()相同，不過需要注意的是Deducer包的加載需要Java環境，沒有安裝Java的電腦可能會加載失敗

續上例：

> chisq.test(table3)Pearson's Chi-squared testdata:  table3
X-squared = 32.237, df = 6, p-value = 1.47e-05Warning message:
In chisq.test(table3) : Chi-squared approximation may be incorrect
#P值<0.05，但是給出了卡方近似可能有誤的警告，結果可能不可信
#更換檢驗函數，使用Deducer包內的likelihood.test()
#這個函數進行似然比獨立檢驗
> library(Deducer)
> likelihood.test(table3)Log likelihood ratio (G-test) test of independence without correctiondata:  table3
Log likelihood ratio statistic (G) = 27.146, X-squared df = 6, p-value = 0.0001359
#P值依然小于0.05，說明種族與幸福確實不獨立

3.3 進行相應分析

????????進行簡單相應分析可以使用MASS包內的corresp()函數，也可以使用ca包中的ca()函數，個人比較推薦使用ca()函數

corresp()用法：corresp(x,nf=1,…)或corresp(x,y,nf=1,…)

????????第一種用法中，參數x是矩陣或數據框，這個函數沒有對表類(table類)對象的用法

????????第二種用法中，x和y都是因子

????????nf指定提取公共因子數量，也就是繪圖時的維度，只有當nf大于或等于2時才能繪制相應分析圖，通常都會取nf=2

????????分析結果直接查看存儲結果的變量即可

ca()用法：ca(obj,…)

????????obj可以是數據框、矩陣、表，本質上是列聯表

????????這個函數會算出相關矩陣的所有特征值，也就是提取出所有公共因子，我們可以根據特征值來看累計貢獻率，以此確定公共因子數。但是這對我們畫圖沒有影響，畫圖默認使用前兩個公共因子

????????分析結果用summary()查看

續上例：

> CA1=corresp(race,happy,nf=2)
> CA2=ca(table3)
> CA1
First canonical correlation(s): 0.13874525 0.04472209 x scores:[,1]        [,2]
1 -0.4450141  0.04605089
2  2.0997831 -1.42379260
3  2.7375930  4.73970128y scores:[,1]       [,2]
1 -0.81133437  0.4891867
2 -0.08354719 -0.2131040
3  2.37903773 -1.0140261
9  4.55423642  9.5915978
> summary(CA2)Principal inertias (eigenvalues):dim    value      %   cum%   scree plot               1      0.019250  90.6  90.6  ***********************  2      0.002000   9.4 100.0  **                       -------- -----                                 Total: 0.021250 100.0                                 Rows:name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
1 |    1 |  833 1000  150 |  -62 999 165 |    2   1   2 |
2 |    2 |  134 1000  563 |  291 954 593 |  -64  46 273 |
3 |    3 |   32 1000  288 |  380 763 242 |  212 237 726 |Columns:name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
1 |    1 |  308 1000  191 | -113 964 203 |   22  36  74 |
2 |    2 |  575 1000    6 |  -12 597   4 |  -10 403  26 |
3 |    3 |  109 1000  568 |  330 981 616 |  -45  19 112 |
4 |    9 |    9 1000  235 |  632 685 178 |  429 315 788 |
#CA1返回的是因子得分，繼續分析需要畫相應分析圖
#關心CA2的維度，發現第二個維度已經解釋了100%的方差

3.4 畫相應分析圖

????????corresp對象的相應分析圖可以用biplot()或plot()畫出，ca對象的相應分析圖只能用plot()畫出，兩個函數都是直接將相應分析結果放入第一個參數即可畫出，不多做介紹

續上例：

> par(mfrow=c(1,2))
> biplot(CA1)
> plot(CA2)

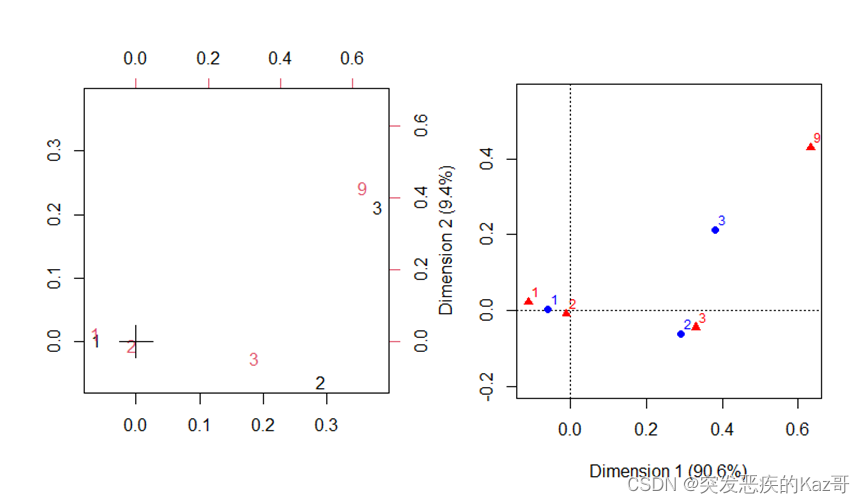
????????左圖是corresp()函數對象的相應分析圖

????????右圖是ca()函數對象的相應分析圖

????????紅色的數字是幸福程度的水平，黑色或藍色的數字表示不同的人種，兩個相應分析圖有些許不同，但是都相似1號人種的幸福程度與1、2很近；2號人種的幸福程度與3比較接近。左圖的3號人種與幸福程度與9很接近，而右圖的3號人種與幸福程度3和9的距離差不多，而且距離相對比較遠，3號人種的幸福程度既較多是3也較多是9

四、小結

????????對各項分析所用到的函數和應用場景進行總結

主成分分析		因子分析
函數	應用場景	函數	應用場景
kmo()	開源獲取，kmo檢驗	kmo()	開源獲取，kmo檢驗
cortest.bartlett()	巴特利特球形檢驗，與kmo檢驗搭配檢查信息重疊度	cortest.bartlett()	巴特利特球形檢驗，與kmo檢驗搭配檢查信息重疊度
princomp()	主成分分析	fa.parallel()	畫碎石圖，確定因子個數
principal()	psych包內的主成分分析	fa()	因子分析
fa.parallel()	畫碎石圖，提前確定主成分個數，對于principal對象
screeplot()	畫碎石圖，確定主成分個數，對于princomp對象
evaluation()	自編，綜合評價

相應分析
函數	應用場景
table()	做列聯表
chisq.test()	獨立性皮爾遜卡方檢驗
likelihood.test()	獨立性似然比卡方檢驗
corresp()	簡單相應分析(MASS)
ca()	簡單相應分析(ca)
plot()	畫相應分析圖
biplot()	畫相應分析圖，對于corresp對象